Order theory

Might be worth a read since it has applicability to Charge Field modeling. Been offline for a bit after installing Linux.
-------
Order theory

Order theory is a branch of mathematics which investigates the intuitive notion of order using binary relations. It provides a formal framework for describing statements such as "this is less than that" or "this precedes that". This article introduces the field and provides basic definitions. A list of order-theoretic terms can be found in the order theory glossary.

https://en.wikipedia.org/wiki/Order_theory
http://www.personal.soton.ac.uk/gan/Roller.pdf



A "good" Hasse diagram

Although Hasse diagrams are simple as well as intuitive tools for dealing with finite posets, it turns out to be rather difficult to draw "good" diagrams. The reason is that there will in general be many possible ways to draw a Hasse diagram for a given poset. The simple technique of just starting with the minimal elements of an order and then drawing greater elements incrementally often produces quite poor results: symmetries and internal structure of the order are easily lost.

The following example demonstrates the issue. Consider the power set of a 4-element set ordered by inclusion ⊆ {\displaystyle \subseteq } \subseteq . Below are four different Hasse diagrams for this partial order. Each subset has a node labelled with a binary encoding that shows whether a certain element is in the subset (1) or not (0):


Upward planarity
Main article: Upward planar drawing
This Hasse diagram of the lattice of subgroups of the dihedral group Dih4 has no crossing edges.



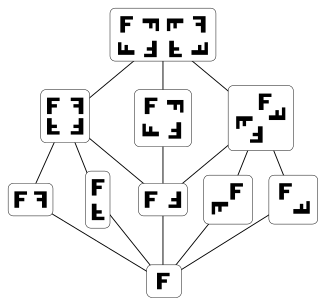
This Hasse diagram of the lattice of subgroups of the dihedral group Dih4 has no crossing edges.

If a partial order can be drawn as a Hasse diagram in which no two edges cross, its covering graph is said to be upward planar. A number of results on upward planarity and on crossing-free Hasse diagram construction are known:

If the partial order to be drawn is a lattice, then it can be drawn without crossings if and only if it has order dimension at most two.[5] In this case, a non-crossing drawing may be found by deriving Cartesian coordinates for the elements from their positions in the two linear orders realizing the order dimension, and then rotating the drawing counterclockwise by a 45-degree angle.
If the partial order has at most one minimal element, or it has at most one maximal element, then it may be tested in linear time whether it has a non-crossing Hasse diagram.[6]
It is NP-complete to determine whether a partial order with multiple sources and sinks can be drawn as a crossing-free Hasse diagram.[7] However, finding a crossing-free Hasse diagram is fixed-parameter tractable when parametrized by the number of articulation points and triconnected components of the transitive reduction of the partial order.[8]
If the y-coordinates of the elements of a partial order are specified, then a crossing-free Hasse diagram respecting those coordinate assignments can be found in linear time, if such a diagram exists.[9] In particular, if the input poset is a graded poset, it is possible to determine in linear time whether there is a crossing-free Hasse diagram in which the height of each vertex is proportional to its rank.

https://en.wikipedia.org/wiki/Hasse_diagram