Possible Charged Particle Field
4 posters
Page 3 of 15
Page 3 of 15 •  1, 2, 3, 4 ... 9 ... 15
1, 2, 3, 4 ... 9 ... 15 
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
.
I've re-tried a 9 particles in a row about 24X earlier today without seeing any overlapped particles. I don't recall ever seeing a single row with overlapped particles. I DO however, see plenty of pushed particles - particles to the right of their finish marks - occur in single rows. There's no evidence that particles have been pushed using my console settings today. I just saw velocity transfers.
I tried two rows next. 18 particles: two rows of nine particles. Both initial velocities equal 30. 20 or so times also without observing overlap. Again, I may see slightly pushed particles.

24 particles: pOne - pEight. Three rows, velocities 10,20,and 30. Finally saw two overlapped particles, shown in the gif above. Particles three and four almost entirely overlap, but separate before both lost their velocities. Particle 5 picked up the same velocity but it pushed particle 6.

Here's an image showing that pushed particle 6.
I submitted a customer service work ticket with bitbucket about twelve hours ago.
Tried using the debugger after normalization, but it would always stop at the very first collision encountered. How to make an exception? So I commented it out.
I trimmed the console output to just the top row's velocity changes. I haven't figured it out yet. The console output follows. The mix of velocity magnitudes of .999s or round integers suggest there may be an easy ( float v.sub( v1 );///? fix but I don't see a direct link between 999s, integer like #s and pushes.
.
Can you reproduce the problem with only a single line of neutrons? Having so many makes it difficult to step through the code or to interpret console output. It doesn't seem like the number of neutrons should matter, but it would be interesting if it did.
I've re-tried a 9 particles in a row about 24X earlier today without seeing any overlapped particles. I don't recall ever seeing a single row with overlapped particles. I DO however, see plenty of pushed particles - particles to the right of their finish marks - occur in single rows. There's no evidence that particles have been pushed using my console settings today. I just saw velocity transfers.
I tried two rows next. 18 particles: two rows of nine particles. Both initial velocities equal 30. 20 or so times also without observing overlap. Again, I may see slightly pushed particles.

24 particles: pOne - pEight. Three rows, velocities 10,20,and 30. Finally saw two overlapped particles, shown in the gif above. Particles three and four almost entirely overlap, but separate before both lost their velocities. Particle 5 picked up the same velocity but it pushed particle 6.

Here's an image showing that pushed particle 6.
I submitted a customer service work ticket with bitbucket about twelve hours ago.
Tried using the debugger after normalization, but it would always stop at the very first collision encountered. How to make an exception? So I commented it out.
I trimmed the console output to just the top row's velocity changes. I haven't figured it out yet. The console output follows. The mix of velocity magnitudes of .999s or round integers suggest there may be an easy ( float v.sub( v1 );///? fix but I don't see a direct link between 999s, integer like #s and pushes.
- Code:
///////////////////////// Collision between particles 1-2
//// pOne velocity lost. From v1=30, v2=0.
cdm.js:746 v1: 30, 0, 0
cdm.js:747 v2: 0, 0, 0
cdm.js:768 a1: -30
cdm.js:769 a2: 0
cdm.js:806 v: -30, 0, 0
//// pTwo velocity increase. v1=0, v2=30.
cdm.js:746 v1: 0, 0, 0
cdm.js:747 v2: 30, 0, 0
cdm.js:768 a1: 0
cdm.js:769 a2: 30
cdm.js:806 v: 30, 0, 0
///////////////////////// Collision between particles 2-3
//// pTwo velocity lost. From v1=30, v2=0.
cdm.js:746 v1: 30, 0, 0
cdm.js:747 v2: 0, 0, 0
cdm.js:768 a1: -29.999999999999996
cdm.js:769 a2: 0
cdm.js:806 v: -29.999999999999993, 0, 0
//// pThree velocity increase. v1=0, v2=30.
cdm.js:746 v1: 0, 0, 0
cdm.js:747 v2: 30, 0, 0
cdm.js:768 a1: 0
cdm.js:769 a2: 29.999999999999996
cdm.js:806 v: 29.999999999999993, 0, 0
///////////////////////// Collision between particles 3-4
//// pThree velocity lost. From v1=30, v2=0.
cdm.js:746 v1: 30, 0, 0
cdm.js:747 v2: 0, 0, 0
cdm.js:768 a1: -30
cdm.js:769 a2: 0
cdm.js:806 v: -30, 0, 0
//// pFour velocity increase. v1=0, v2=30.
cdm.js:746 v1: 0, 0, 0
cdm.js:747 v2: 30, 0, 0
cdm.js:768 a1: 0
cdm.js:769 a2: 30
cdm.js:806 v: 30, 0, 0
///Pattern break.
cdm.js:746 v1: 0, 0, 0
cdm.js:747 v2: 30, 0, 0
cdm.js:768 a1: 0
cdm.js:769 a2: -30
cdm.js:806 v: 30, 0, 0
cdm.js:746 v1: 30, 0, 0
cdm.js:747 v2: 0, 0, 0
cdm.js:768 a1: 30
cdm.js:769 a2: 0
cdm.js:806 v: -30, 0, 0
cdm.js:746 v1: 30, 0, 0
cdm.js:747 v2: 0, 0, 0
cdm.js:768 a1: -30
cdm.js:769 a2: 0
cdm.js:806 v: -30, 0, 0
cdm.js:746 v1: 0, 0, 0
cdm.js:747 v2: 30, 0, 0
cdm.js:768 a1: 0
cdm.js:769 a2: 30
cdm.js:806 v: 30, 0, 0
cdm.js:746 v1: 0, 0, 0
cdm.js:747 v2: 30, 0, 0
cdm.js:768 a1: 0
cdm.js:769 a2: -30
cdm.js:806 v: 30, 0, 0
cdm.js:746 v1: 30, 0, 0
cdm.js:747 v2: 0, 0, 0
cdm.js:768 a1: 30
cdm.js:769 a2: 0
cdm.js:806 v: -30, 0, 0
cdm.js:746 v1: 30, 0, 0
cdm.js:747 v2: 0, 0, 0
cdm.js:768 a1: -30
cdm.js:769 a2: 0
cdm.js:806 v: -30, 0, 0
cdm.js:746 v1: 0, 0, 0
cdm.js:747 v2: 30, 0, 0
cdm.js:768 a1: 0
cdm.js:769 a2: 30
cdm.js:806 v: 30, 0, 0
cdm.js:746 v1: 0, 0, 0
cdm.js:747 v2: 30, 0, 0
cdm.js:768 a1: 0
cdm.js:769 a2: -30
cdm.js:806 v: 30, 0, 0
cdm.js:746 v1: 30, 0, 0
cdm.js:747 v2: 0, 0, 0
cdm.js:768 a1: 30
cdm.js:769 a2: 0
cdm.js:806 v: -30, 0, 0
cdm.js:746 v1: 30, 0, 0
cdm.js:747 v2: 0, 0, 0
cdm.js:768 a1: -30
cdm.js:769 a2: 0
cdm.js:806 v: -30, 0, 0
cdm.js:746 v1: 0, 0, 0
cdm.js:747 v2: 30, 0, 0
cdm.js:768 a1: 0
cdm.js:769 a2: 30
cdm.js:806 v: 30, 0, 0
cdm.js:746 v1: 0, 0, 0
cdm.js:747 v2: 30, 0, 0
cdm.js:768 a1: 0
cdm.js:769 a2: -29.999999999999996
cdm.js:806 v: 29.999999999999993, 0, 0
cdm.js:746 v1: 30, 0, 0
cdm.js:747 v2: 0, 0, 0
cdm.js:768 a1: 29.999999999999996
cdm.js:769 a2: 0
cdm.js:806 v: -29.999999999999993, 0, 0
cdm.js:746 v1: 30, 0, 0
cdm.js:747 v2: 0, 0, 0
cdm.js:768 a1: -30
cdm.js:769 a2: 0
cdm.js:806 v: -30, 0, 0
cdm.js:746 v1: 0, 0, 0
cdm.js:747 v2: 30, 0, 0
cdm.js:768 a1: 0
cdm.js:769 a2: 30
cdm.js:806 v: 30, 0, 0
cdm.js:746 v1: 0, 0, 0
cdm.js:747 v2: 30, 0, 0
cdm.js:768 a1: 0
cdm.js:769 a2: -30
cdm.js:806 v: 30, 0, 0
cdm.js:746 v1: 30, 0, 0
cdm.js:747 v2: 0, 0, 0
cdm.js:768 a1: 30
cdm.js:769 a2: 0
cdm.js:806 v: -30, 0, 0
cdm.js:746 v1: 30, 0, 0
cdm.js:747 v2: 0, 0, 0
cdm.js:768 a1: -30
cdm.js:769 a2: 0
cdm.js:806 v: -30, 0, 0
cdm.js:746 v1: 0, 0, 0
cdm.js:747 v2: 30, 0, 0
cdm.js:768 a1: 0
cdm.js:769 a2: 30
cdm.js:806 v: 30, 0, 0
cdm.js:746 v1: 0, 0, 0
cdm.js:747 v2: 30, 0, 0
cdm.js:768 a1: 0
cdm.js:769 a2: -29.999999999999996
cdm.js:806 v: 29.999999999999993, 0, 0
cdm.js:746 v1: 30, 0, 0
cdm.js:747 v2: 0, 0, 0
cdm.js:768 a1: 29.999999999999996
cdm.js:769 a2: 0
cdm.js:806 v: -29.999999999999993, 0, 0
cdm.js:746 v1: 30, 0, 0
cdm.js:747 v2: 0, 0, 0
cdm.js:768 a1: -30
cdm.js:769 a2: 0
cdm.js:806 v: -30, 0, 0
cdm.js:746 v1: 0, 0, 0
cdm.js:747 v2: 30, 0, 0
cdm.js:768 a1: 0
cdm.js:769 a2: 30
cdm.js:806 v: 30, 0, 0
cdm.js:746 v1: 0, 0, 0
cdm.js:747 v2: 30, 0, 0
cdm.js:768 a1: 0
cdm.js:769 a2: -30
cdm.js:806 v: 30, 0, 0
cdm.js:746 v1: 30, 0, 0
cdm.js:747 v2: 0, 0, 0
cdm.js:768 a1: 30
cdm.js:769 a2: 0
cdm.js:806 v: -30, 0, 0
cdm.js:746 v1: 30, 0, 0
cdm.js:747 v2: 0, 0, 0
cdm.js:768 a1: 30
cdm.js:769 a2: 0
cdm.js:806 v: -30, 0, 0
cdm.js:746 v1: 0, 0, 0
cdm.js:747 v2: 30, 0, 0
cdm.js:768 a1: 0
cdm.js:769 a2: -30
cdm.js:806 v: 30, 0, 0
cdm.js:746 v1: 0, 0, 0
cdm.js:747 v2: 30, 0, 0
cdm.js:768 a1: 0
cdm.js:769 a2: -30
cdm.js:806 v: 30, 0, 0
cdm.js:746 v1: 30, 0, 0
cdm.js:747 v2: 0, 0, 0
cdm.js:768 a1: 30
cdm.js:769 a2: 0
cdm.js:806 v: -30, 0, 0
cdm.js:746 v1: 30, 0, 0
cdm.js:747 v2: 0, 0, 0
cdm.js:768 a1: 30
cdm.js:769 a2: 0
cdm.js:806 v: -30, 0, 0
cdm.js:746 v1: 0, 0, 0
cdm.js:747 v2: 30, 0, 0
cdm.js:768 a1: 0
cdm.js:769 a2: -30
cdm.js:806 v: 30, 0, 0
cdm.js:746 v1: 0, 0, 0
cdm.js:747 v2: 30, 0, 0
cdm.js:768 a1: 0
cdm.js:769 a2: -30
cdm.js:806 v: 30, 0, 0
cdm.js:746 v1: 30, 0, 0
cdm.js:747 v2: 0, 0, 0
cdm.js:768 a1: 30
cdm.js:769 a2: 0
cdm.js:806 v: -30, 0, 0
cdm.js:746 v1: 30, 0, 0
cdm.js:747 v2: 0, 0, 0
cdm.js:768 a1: -30
cdm.js:769 a2: 0
cdm.js:806 v: -30, 0, 0
cdm.js:746 v1: 0, 0, 0
cdm.js:747 v2: 30, 0, 0
cdm.js:768 a1: 0
cdm.js:769 a2: 30
cdm.js:806 v: 30, 0, 0
///////////////////////// Collision between particles 4-5
cdm.js:746 v1: 30, 0, 0
cdm.js:747 v2: 0, 0, 0
cdm.js:768 a1: -30
cdm.js:769 a2: 0
cdm.js:806 v: -30, 0, 0
cdm.js:746 v1: 0, 0, 0
cdm.js:747 v2: 30, 0, 0
cdm.js:768 a1: 0
cdm.js:769 a2: 30
cdm.js:806 v: 30, 0, 0
///////////////////////// Collision between particles 5-6
cdm.js:746 v1: 30, 0, 0
cdm.js:747 v2: 0, 0, 0
cdm.js:768 a1: -30
cdm.js:769 a2: 0
cdm.js:806 v: -30, 0, 0
cdm.js:746 v1: 0, 0, 0
cdm.js:747 v2: 30, 0, 0
cdm.js:768 a1: 0
cdm.js:769 a2: 30
cdm.js:806 v: 30, 0, 0
///////////////////////// Collision between particles 6-7
cdm.js:746 v1: 30, 0, 0
cdm.js:747 v2: 0, 0, 0
cdm.js:768 a1: -30
cdm.js:769 a2: 0
cdm.js:806 v: -30, 0, 0
cdm.js:746 v1: 0, 0, 0
cdm.js:747 v2: 30, 0, 0
cdm.js:768 a1: 0
cdm.js:769 a2: 30
cdm.js:806 v: 30, 0, 0
///////////////////////// Collision between particles 7-8
cdm.js:746 v1: 30, 0, 0
cdm.js:747 v2: 0, 0, 0
cdm.js:768 a1: -29.999999999999996
cdm.js:769 a2: 0
cdm.js:806 v: -29.999999999999993, 0, 0
cdm.js:746 v1: 0, 0, 0
cdm.js:747 v2: 30, 0, 0
cdm.js:768 a1: 0
cdm.js:769 a2: 29.999999999999996
cdm.js:806 v: 29.999999999999993, 0, 0
.
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
Don't worry about those 29.99999999996 type values. They are just rounding errors in the math. Nothing we can do about it that does not involve more expensive operations (by using higher precision numbers). They are annoying, and they will leave residual velocities where there shouldn't be, but they will be so small as to be unnoticeable unless you just leave it sitting there for a really long time and eventually notice that a particle you thought wasn't moving, has actually moved. They certainly aren't causing our problem.
All of that console output looks fine. Did you actually see an error happen while that output was being generated? I really need to see it when there is an error.
All of that console output looks fine. Did you actually see an error happen while that output was being generated? I really need to see it when there is an error.
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
All of that console output looks fine. Did you actually see an error happen while that output was being generated? I really need to see it when there is an error.
Correct, although that output isn't fine, it's filled with many additional velocity changes, the twitches you observed in overlapped particles. The gif and console output are from the same collision error event which I observed. I still have it on my browser. I was grateful to find such a compact event. All other collision errors console outputs I observed were much longer, 1 or 2 thousand lines. It's remarkable that all such overlapping events I observed involved the same velocities - just the initial velocities from that row.
I'll try to find a collision error that involves a velocity different from the initial row velocity tomorrow.
.
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
I don't see an errors in that output. Can you point out what you see?
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
.
Sorry I wasn't clear. An eight particle row without any collision errors results in 7 collisions with a total of 14 velocity changes. In the console output above, I inserted some commentary. The error involves the 36 velocity changes after "Collision between particles 3-4"... "pattern break" and "Collision between particles 4-5". All those velocity changes involve 30, 0 and -30 velocities. I suppose unequal numbers of those velocities may add up to fractional speeds, but I don't see how particles can move faster than just those velocities, so that's the error case I'll look for tomorrow.
.
Sorry I wasn't clear. An eight particle row without any collision errors results in 7 collisions with a total of 14 velocity changes. In the console output above, I inserted some commentary. The error involves the 36 velocity changes after "Collision between particles 3-4"... "pattern break" and "Collision between particles 4-5". All those velocity changes involve 30, 0 and -30 velocities. I suppose unequal numbers of those velocities may add up to fractional speeds, but I don't see how particles can move faster than just those velocities, so that's the error case I'll look for tomorrow.
.
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
I don't think that is correct. The output will follow the algorithm. Add another console.log at the start of the calculateCollision method that writes the index1 and index2 values for you. Then you know which particles are interacting.
console.log( 'P1: ' + index1 + ', P2: ' + index2 );
console.log( 'P1: ' + index1 + ', P2: ' + index2 );
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
Basically, the twitching happens across multiple frames, never within the same frame as your interpretation of the output would suggest.
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
Unless those are the only colliding particles, then you would be correct. I don't know right now. It is suggesting that the change in velocity is not being added to the position of the particles under some circumstances. I'll have a look into that code tonight.
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
No luck.
I didn't find any problems with the addition of velocities or updating the position with that velocity. I added in some console.logs to make sure that things were executing as I thought they should be, and they were. I then decided to re-write the algorithm without using the internal memory buffers, so that it would just retrieve the position, orientation, velocity and spin from the Particle object itself (which will be faster), but that didn't help either.
The main reason I did that was because the memory buffers use a Float32Array object, which are 32bit floats, not 64bit floats, and it might be a number precision problem. It wasn't. I will probably factor that code in anyway, just for the performance gain and I don't think we can use shaders in the way that I wanted to so they are not needed. I keep finding conflicting information about using shaders and don't know what to believe at the moment.
I'm nearly at the point where I want to use a different collision algorithm.
I didn't find any problems with the addition of velocities or updating the position with that velocity. I added in some console.logs to make sure that things were executing as I thought they should be, and they were. I then decided to re-write the algorithm without using the internal memory buffers, so that it would just retrieve the position, orientation, velocity and spin from the Particle object itself (which will be faster), but that didn't help either.
The main reason I did that was because the memory buffers use a Float32Array object, which are 32bit floats, not 64bit floats, and it might be a number precision problem. It wasn't. I will probably factor that code in anyway, just for the performance gain and I don't think we can use shaders in the way that I wanted to so they are not needed. I keep finding conflicting information about using shaders and don't know what to believe at the moment.
I'm nearly at the point where I want to use a different collision algorithm.
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
With respect to your SourceTree issues, have you updated the app? Does it need an update? There is a flag in the top right corner of the app (on Windows, Mac may be different) and if it is orange, then it wants you to look at it. Sometimes it is just some question but it may be an update notification. I think there were some major updates recently and they required me to login in via the website before SourceTree would login again.
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
.
WARNING. A lot of ugly follows. Nevyn, you don't sound like you're enjoying yourself, maybe you shouldn't look.

Collision error. Below, A 2X5 collision grid is shown, with particles left to right P0 – P4 on the bottom row, and P5 – P9 on the top - complying with their actual index numbers as referred to in the console output. The horizontal distance between particles is 10, vertical separation is 7.5. P0 is given an initial velocity, v = 30. The top row’s leftmost particle, P5 is given an initial v = 40. The error collision – overlapped particles - occurred in the top row. The bottom row contains 3 pushed particles – a problem which doesn’t seem to be indicated by the current console output. The image below is self-explanatory. The above gif and following closeup details show just the center portion of the top row – the area is shown by the yellow rectangle.
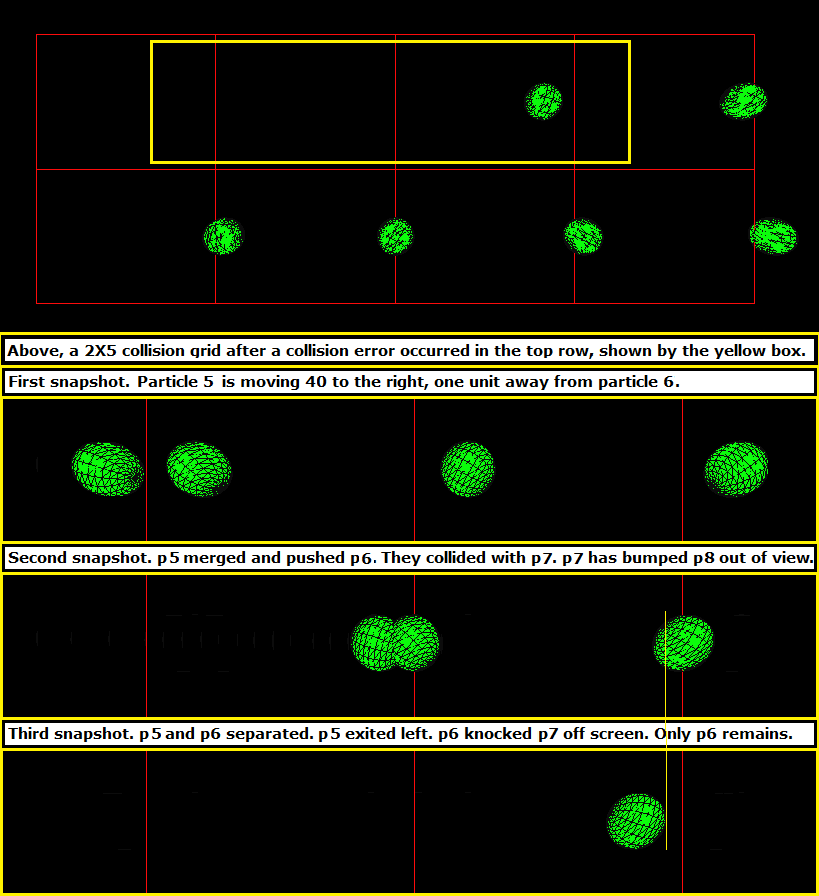
The particle numbers have been changed from my previous descriptions on order to agree with the console output. The thin yellow line at the bottom right shows that p2 pushed p3 before the velocity transfers occurred.
Note that p5 slides under p6 about halfway before p6 joins in and movs to the right. P7/P8 looks to be the one clean collision that occurred in the top row. Three of the four particles in the second row are pushed.
I’ll post the Console output in the next post or two.
.
WARNING. A lot of ugly follows. Nevyn, you don't sound like you're enjoying yourself, maybe you shouldn't look.

Collision error. Below, A 2X5 collision grid is shown, with particles left to right P0 – P4 on the bottom row, and P5 – P9 on the top - complying with their actual index numbers as referred to in the console output. The horizontal distance between particles is 10, vertical separation is 7.5. P0 is given an initial velocity, v = 30. The top row’s leftmost particle, P5 is given an initial v = 40. The error collision – overlapped particles - occurred in the top row. The bottom row contains 3 pushed particles – a problem which doesn’t seem to be indicated by the current console output. The image below is self-explanatory. The above gif and following closeup details show just the center portion of the top row – the area is shown by the yellow rectangle.

The particle numbers have been changed from my previous descriptions on order to agree with the console output. The thin yellow line at the bottom right shows that p2 pushed p3 before the velocity transfers occurred.
Note that p5 slides under p6 about halfway before p6 joins in and movs to the right. P7/P8 looks to be the one clean collision that occurred in the top row. Three of the four particles in the second row are pushed.
I’ll post the Console output in the next post or two.
.
Last edited by LongtimeAirman on Thu Aug 09, 2018 10:19 pm; edited 1 time in total
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
.
Console output. Each row of 5 particles should result in just 4 collisions, (5-1); times 2 rows, for a total of eight collisions. Given the output variables required at every collision: v1, v2, P1, P2, a1, a2, and v, every non-error collision requires 12 console output lines. We would expect 8*12 or 96 output lines for 8 error free collisions. In this case, row 2 collisions make up 48 lines of the console output. The total number of lines, after removing the line 1 three,js, from the top the console output is exactly 1,000. That would be equal to 1000/12 = 83.33 collisions. That’s my rough summary, I no doubt have details wrong. I concentrated on presentation, I also need to study it. For example; Why is P1: 6, P2: 7 the first collision, shouldn’t it be P1: 5 and P2: 6?? I’ll place a copy of the console output into my GitFolder, but I guess it won’t be pushed for some time. So, without further ado.
I hope you'll be requesting position locations next?
Thanks for that Sourcetree idea, I'll look into it.
.
Console output. Each row of 5 particles should result in just 4 collisions, (5-1); times 2 rows, for a total of eight collisions. Given the output variables required at every collision: v1, v2, P1, P2, a1, a2, and v, every non-error collision requires 12 console output lines. We would expect 8*12 or 96 output lines for 8 error free collisions. In this case, row 2 collisions make up 48 lines of the console output. The total number of lines, after removing the line 1 three,js, from the top the console output is exactly 1,000. That would be equal to 1000/12 = 83.33 collisions. That’s my rough summary, I no doubt have details wrong. I concentrated on presentation, I also need to study it. For example; Why is P1: 6, P2: 7 the first collision, shouldn’t it be P1: 5 and P2: 6?? I’ll place a copy of the console output into my GitFolder, but I guess it won’t be pushed for some time. So, without further ado.
- Code:
cdm.js:748 v2: 0, 0, 0
cdm.js:769 a1: 40
cdm.js:770 a2: 0
cdm.js:807 v: -40, 0, 0
cdm.js:746 P1: 6, P2: 7
cdm.js:747 v1: 40, 0, 0
cdm.js:748 v2: 0, 0, 0
cdm.js:769 a1: -40
cdm.js:770 a2: 0
cdm.js:807 v: -40, 0, 0
cdm.js:746 P1: 7, P2: 6
cdm.js:747 v1: 0, 0, 0
cdm.js:748 v2: 40, 0, 0
cdm.js:769 a1: 0
cdm.js:770 a2: 40
cdm.js:807 v: 40, 0, 0
cdm.js:746 P1: 5, P2: 6
cdm.js:747 v1: 40, 0, 0
cdm.js:748 v2: -40, 0, 0
cdm.js:769 a1: -40
cdm.js:770 a2: 40
cdm.js:807 v: -80, 0, 0
cdm.js:746 P1: 6, P2: 5
cdm.js:747 v1: -40, 0, 0
cdm.js:748 v2: 40, 0, 0
cdm.js:769 a1: -40
cdm.js:770 a2: 40
cdm.js:807 v: 80, 0, 0
cdm.js:746 P1: 5, P2: 6
cdm.js:747 v1: -40, 0, 0
cdm.js:748 v2: 40, 0, 0
cdm.js:769 a1: 40
cdm.js:770 a2: -40
cdm.js:807 v: 80, 0, 0
cdm.js:746 P1: 6, P2: 5
cdm.js:747 v1: 40, 0, 0
cdm.js:748 v2: -40, 0, 0
cdm.js:769 a1: 40
cdm.js:770 a2: -40
cdm.js:807 v: -80, 0, 0
cdm.js:746 P1: 5, P2: 6
cdm.js:747 v1: 40, 0, 0
cdm.js:748 v2: -40, 0, 0
cdm.js:769 a1: -40
cdm.js:770 a2: 40
cdm.js:807 v: -80, 0, 0
cdm.js:746 P1: 6, P2: 5
cdm.js:747 v1: -40, 0, 0
cdm.js:748 v2: 40, 0, 0
cdm.js:769 a1: -40
cdm.js:770 a2: 40
cdm.js:807 v: 80, 0, 0
cdm.js:746 P1: 5, P2: 6
cdm.js:747 v1: -40, 0, 0
cdm.js:748 v2: 40, 0, 0
cdm.js:769 a1: 40
cdm.js:770 a2: -40
cdm.js:807 v: 80, 0, 0
cdm.js:746 P1: 6, P2: 5
cdm.js:747 v1: 40, 0, 0
cdm.js:748 v2: -40, 0, 0
cdm.js:769 a1: 40
cdm.js:770 a2: -40
cdm.js:807 v: -80, 0, 0
cdm.js:746 P1: 5, P2: 6
cdm.js:747 v1: 40, 0, 0
cdm.js:748 v2: -40, 0, 0
cdm.js:769 a1: 40
cdm.js:770 a2: -40
cdm.js:807 v: -80, 0, 0
cdm.js:746 P1: 6, P2: 5
cdm.js:747 v1: -40, 0, 0
cdm.js:748 v2: 40, 0, 0
cdm.js:769 a1: 40
cdm.js:770 a2: -40
cdm.js:807 v: 80, 0, 0
cdm.js:746 P1: 5, P2: 6
cdm.js:747 v1: -40, 0, 0
cdm.js:748 v2: 40, 0, 0
cdm.js:769 a1: 40
cdm.js:770 a2: -40
cdm.js:807 v: 80, 0, 0
cdm.js:746 P1: 6, P2: 5
cdm.js:747 v1: 40, 0, 0
cdm.js:748 v2: -40, 0, 0
cdm.js:769 a1: 40
cdm.js:770 a2: -40
cdm.js:807 v: -80, 0, 0
cdm.js:746 P1: 5, P2: 6
cdm.js:747 v1: 40, 0, 0
cdm.js:748 v2: -40, 0, 0
cdm.js:769 a1: 40
cdm.js:770 a2: -40
cdm.js:807 v: -80, 0, 0
cdm.js:746 P1: 6, P2: 5
cdm.js:747 v1: -40, 0, 0
cdm.js:748 v2: 40, 0, 0
cdm.js:769 a1: 40
cdm.js:770 a2: -40
cdm.js:807 v: 80, 0, 0
cdm.js:746 P1: 5, P2: 6
cdm.js:747 v1: -40, 0, 0
cdm.js:748 v2: 40, 0, 0
cdm.js:769 a1: 40
cdm.js:770 a2: -40
cdm.js:807 v: 80, 0, 0
cdm.js:746 P1: 6, P2: 5
cdm.js:747 v1: 40, 0, 0
cdm.js:748 v2: -40, 0, 0
cdm.js:769 a1: 40
cdm.js:770 a2: -40
cdm.js:807 v: -80, 0, 0
cdm.js:746 P1: 5, P2: 6
cdm.js:747 v1: 40, 0, 0
cdm.js:748 v2: -40, 0, 0
cdm.js:769 a1: 40
cdm.js:770 a2: -40
cdm.js:807 v: -80, 0, 0
cdm.js:746 P1: 6, P2: 5
cdm.js:747 v1: -40, 0, 0
cdm.js:748 v2: 40, 0, 0
cdm.js:769 a1: 40
cdm.js:770 a2: -40
cdm.js:807 v: 80, 0, 0
cdm.js:746 P1: 5, P2: 6
cdm.js:747 v1: -40, 0, 0
cdm.js:748 v2: 40, 0, 0
cdm.js:769 a1: 40
cdm.js:770 a2: -40
cdm.js:807 v: 80, 0, 0
cdm.js:746 P1: 6, P2: 5
cdm.js:747 v1: 40, 0, 0
cdm.js:748 v2: -40, 0, 0
cdm.js:769 a1: 40
cdm.js:770 a2: -40
cdm.js:807 v: -80, 0, 0
cdm.js:746 P1: 5, P2: 6
cdm.js:747 v1: 40, 0, 0
cdm.js:748 v2: -40, 0, 0
cdm.js:769 a1: 40
cdm.js:770 a2: -40
cdm.js:807 v: -80, 0, 0
cdm.js:746 P1: 6, P2: 5
cdm.js:747 v1: -40, 0, 0
cdm.js:748 v2: 40, 0, 0
cdm.js:769 a1: 40
cdm.js:770 a2: -40
cdm.js:807 v: 80, 0, 0
cdm.js:746 P1: 5, P2: 6
cdm.js:747 v1: -40, 0, 0
cdm.js:748 v2: 40, 0, 0
cdm.js:769 a1: 40
cdm.js:770 a2: -40
cdm.js:807 v: 80, 0, 0
cdm.js:746 P1: 6, P2: 5
cdm.js:747 v1: 40, 0, 0
cdm.js:748 v2: -40, 0, 0
cdm.js:769 a1: 40
cdm.js:770 a2: -40
cdm.js:807 v: -80, 0, 0
cdm.js:746 P1: 7, P2: 8
cdm.js:747 v1: 40, 0, 0
cdm.js:748 v2: 0, 0, 0
cdm.js:769 a1: -40
cdm.js:770 a2: 0
cdm.js:807 v: -40, 0, 0
cdm.js:746 P1: 8, P2: 7
cdm.js:747 v1: 0, 0, 0
cdm.js:748 v2: 40, 0, 0
cdm.js:769 a1: 0
cdm.js:770 a2: 40
cdm.js:807 v: 40, 0, 0
cdm.js:746 P1: 2, P2: 3
cdm.js:747 v1: 30, 0, 0
cdm.js:748 v2: 0, 0, 0
cdm.js:769 a1: -30
cdm.js:770 a2: 0
cdm.js:807 v: -30, 0, 0
cdm.js:746 P1: 3, P2: 2
cdm.js:747 v1: 0, 0, 0
cdm.js:748 v2: 30, 0, 0
cdm.js:769 a1: 0
cdm.js:770 a2: 30
cdm.js:807 v: 30, 0, 0
cdm.js:746 P1: 5, P2: 6
cdm.js:747 v1: 40, 0, 0
cdm.js:748 v2: -40, 0, 0
cdm.js:769 a1: 40
cdm.js:770 a2: -40
cdm.js:807 v: -80, 0, 0
cdm.js:746 P1: 6, P2: 5
cdm.js:747 v1: -40, 0, 0
cdm.js:748 v2: 40, 0, 0
cdm.js:769 a1: 40
cdm.js:770 a2: -40
cdm.js:807 v: 80, 0, 0
cdm.js:746 P1: 5, P2: 6
cdm.js:747 v1: -40, 0, 0
cdm.js:748 v2: 40, 0, 0
cdm.js:769 a1: 40
cdm.js:770 a2: -40
cdm.js:807 v: 80, 0, 0
cdm.js:746 P1: 6, P2: 5
cdm.js:747 v1: 40, 0, 0
cdm.js:748 v2: -40, 0, 0
cdm.js:769 a1: 40
cdm.js:770 a2: -40
cdm.js:807 v: -80, 0, 0
cdm.js:746 P1: 5, P2: 6
cdm.js:747 v1: 40, 0, 0
cdm.js:748 v2: -40, 0, 0
cdm.js:769 a1: -40
cdm.js:770 a2: 40
cdm.js:807 v: -80, 0, 0
cdm.js:746 P1: 6, P2: 5
cdm.js:747 v1: -40, 0, 0
cdm.js:748 v2: 40, 0, 0
cdm.js:769 a1: -40
cdm.js:770 a2: 40
cdm.js:807 v: 80, 0, 0
cdm.js:746 P1: 5, P2: 6
cdm.js:747 v1: -40, 0, 0
cdm.js:748 v2: 40, 0, 0
cdm.js:769 a1: 40
cdm.js:770 a2: -40
cdm.js:807 v: 80, 0, 0
cdm.js:746 P1: 6, P2: 5
cdm.js:747 v1: 40, 0, 0
cdm.js:748 v2: -40, 0, 0
cdm.js:769 a1: 40
cdm.js:770 a2: -40
cdm.js:807 v: -80, 0, 0
cdm.js:746 P1: 5, P2: 6
cdm.js:747 v1: 40, 0, 0
cdm.js:748 v2: -40, 0, 0
cdm.js:769 a1: 40
cdm.js:770 a2: -40
cdm.js:807 v: -80, 0, 0
cdm.js:746 P1: 6, P2: 5
cdm.js:747 v1: -40, 0, 0
cdm.js:748 v2: 40, 0, 0
cdm.js:769 a1: 40
cdm.js:770 a2: -40
cdm.js:807 v: 80, 0, 0
cdm.js:746 P1: 5, P2: 6
cdm.js:747 v1: -40, 0, 0
cdm.js:748 v2: 40, 0, 0
cdm.js:769 a1: 40
cdm.js:770 a2: -40
cdm.js:807 v: 80, 0, 0
cdm.js:746 P1: 6, P2: 5
cdm.js:747 v1: 40, 0, 0
cdm.js:748 v2: -40, 0, 0
cdm.js:769 a1: 40
cdm.js:770 a2: -40
cdm.js:807 v: -80, 0, 0
cdm.js:746 P1: 5, P2: 6
cdm.js:747 v1: 40, 0, 0
cdm.js:748 v2: -40, 0, 0
cdm.js:769 a1: -40
cdm.js:770 a2: 40
cdm.js:807 v: -80, 0, 0
cdm.js:746 P1: 6, P2: 5
cdm.js:747 v1: -40, 0, 0
cdm.js:748 v2: 40, 0, 0
cdm.js:769 a1: -40
cdm.js:770 a2: 40
cdm.js:807 v: 80, 0, 0
cdm.js:746 P1: 5, P2: 6
cdm.js:747 v1: -40, 0, 0
cdm.js:748 v2: 40, 0, 0
cdm.js:769 a1: 40
cdm.js:770 a2: -40
cdm.js:807 v: 80, 0, 0
cdm.js:746 P1: 6, P2: 5
cdm.js:747 v1: 40, 0, 0
cdm.js:748 v2: -40, 0, 0
cdm.js:769 a1: 40
cdm.js:770 a2: -40
cdm.js:807 v: -80, 0, 0
cdm.js:746 P1: 5, P2: 6
cdm.js:747 v1: 40, 0, 0
cdm.js:748 v2: -40, 0, 0
cdm.js:769 a1: -40
cdm.js:770 a2: 40
cdm.js:807 v: -80, 0, 0
cdm.js:746 P1: 6, P2: 5
cdm.js:747 v1: -40, 0, 0
cdm.js:748 v2: 40, 0, 0
cdm.js:769 a1: -40
cdm.js:770 a2: 40
cdm.js:807 v: 80, 0, 0
cdm.js:746 P1: 5, P2: 6
cdm.js:747 v1: -40, 0, 0
cdm.js:748 v2: 40, 0, 0
cdm.js:769 a1: 40
cdm.js:770 a2: -40
cdm.js:807 v: 80, 0, 0
cdm.js:746 P1: 6, P2: 5
cdm.js:747 v1: 40, 0, 0
cdm.js:748 v2: -40, 0, 0
cdm.js:769 a1: 40
cdm.js:770 a2: -40
cdm.js:807 v: -80, 0, 0
cdm.js:746 P1: 5, P2: 6
cdm.js:747 v1: 40, 0, 0
cdm.js:748 v2: -40, 0, 0
cdm.js:769 a1: -40
cdm.js:770 a2: 40
cdm.js:807 v: -80, 0, 0
cdm.js:746 P1: 6, P2: 5
cdm.js:747 v1: -40, 0, 0
cdm.js:748 v2: 40, 0, 0
cdm.js:769 a1: -40
cdm.js:770 a2: 40
cdm.js:807 v: 80, 0, 0
cdm.js:746 P1: 5, P2: 6
cdm.js:747 v1: -40, 0, 0
cdm.js:748 v2: 40, 0, 0
cdm.js:769 a1: 40
cdm.js:770 a2: -40
cdm.js:807 v: 80, 0, 0
cdm.js:746 P1: 6, P2: 5
cdm.js:747 v1: 40, 0, 0
cdm.js:748 v2: -40, 0, 0
cdm.js:769 a1: 40
cdm.js:770 a2: -40
cdm.js:807 v: -80, 0, 0
cdm.js:746 P1: 8, P2: 9
cdm.js:747 v1: 40, 0, 0
cdm.js:748 v2: 0, 0, 0
cdm.js:769 a1: -40
cdm.js:770 a2: 0
cdm.js:807 v: -40, 0, 0
cdm.js:746 P1: 9, P2: 8
cdm.js:747 v1: 0, 0, 0
cdm.js:748 v2: 40, 0, 0
cdm.js:769 a1: 0
cdm.js:770 a2: 40
cdm.js:807 v: 40, 0, 0
cdm.js:746 P1: 5, P2: 6
cdm.js:747 v1: 40, 0, 0
cdm.js:748 v2: -40, 0, 0
cdm.js:769 a1: -40
cdm.js:770 a2: 40
cdm.js:807 v: -80, 0, 0
cdm.js:746 P1: 6, P2: 5
cdm.js:747 v1: -40, 0, 0
cdm.js:748 v2: 40, 0, 0
cdm.js:769 a1: -40
cdm.js:770 a2: 40
cdm.js:807 v: 80, 0, 0
cdm.js:746 P1: 5, P2: 6
cdm.js:747 v1: -40, 0, 0
cdm.js:748 v2: 40, 0, 0
cdm.js:769 a1: 40
cdm.js:770 a2: -40
cdm.js:807 v: 80, 0, 0
cdm.js:746 P1: 6, P2: 5
cdm.js:747 v1: 40, 0, 0
cdm.js:748 v2: -40, 0, 0
cdm.js:769 a1: 40
cdm.js:770 a2: -40
cdm.js:807 v: -80, 0, 0
cdm.js:746 P1: 5, P2: 6
cdm.js:747 v1: 40, 0, 0
cdm.js:748 v2: -40, 0, 0
cdm.js:769 a1: 40
cdm.js:770 a2: -40
cdm.js:807 v: -80, 0, 0
cdm.js:746 P1: 6, P2: 5
cdm.js:747 v1: -40, 0, 0
cdm.js:748 v2: 40, 0, 0
cdm.js:769 a1: 40
cdm.js:770 a2: -40
cdm.js:807 v: 80, 0, 0
cdm.js:746 P1: 5, P2: 6
cdm.js:747 v1: -40, 0, 0
cdm.js:748 v2: 40, 0, 0
cdm.js:769 a1: 40
cdm.js:770 a2: -40
cdm.js:807 v: 80, 0, 0
cdm.js:746 P1: 6, P2: 5
cdm.js:747 v1: 40, 0, 0
cdm.js:748 v2: -40, 0, 0
cdm.js:769 a1: 40
cdm.js:770 a2: -40
cdm.js:807 v: -80, 0, 0
cdm.js:746 P1: 5, P2: 6
cdm.js:747 v1: 40, 0, 0
cdm.js:748 v2: -40, 0, 0
cdm.js:769 a1: 40
cdm.js:770 a2: -40
cdm.js:807 v: -80, 0, 0
cdm.js:746 P1: 6, P2: 5
cdm.js:747 v1: -40, 0, 0
cdm.js:748 v2: 40, 0, 0
cdm.js:769 a1: 40
cdm.js:770 a2: -40
cdm.js:807 v: 80, 0, 0
cdm.js:746 P1: 3, P2: 4
cdm.js:747 v1: 30, 0, 0
cdm.js:748 v2: 0, 0, 0
cdm.js:769 a1: -30
cdm.js:770 a2: 0
cdm.js:807 v: -30, 0, 0
cdm.js:746 P1: 4, P2: 3
cdm.js:747 v1: 0, 0, 0
cdm.js:748 v2: 30, 0, 0
cdm.js:769 a1: 0
cdm.js:770 a2: 30
cdm.js:807 v: 30, 0, 0
cdm.js:746 P1: 5, P2: 6
cdm.js:747 v1: -40, 0, 0
cdm.js:748 v2: 40, 0, 0
cdm.js:769 a1: 40
cdm.js:770 a2: -40
cdm.js:807 v: 80, 0, 0
cdm.js:746 P1: 6, P2: 5
cdm.js:747 v1: 40, 0, 0
cdm.js:748 v2: -40, 0, 0
cdm.js:769 a1: 40
cdm.js:770 a2: -40
cdm.js:807 v: -80, 0, 0
cdm.js:746 P1: 3, P2: 4
cdm.js:747 v1: 0, 0, 0
cdm.js:748 v2: 30, 0, 0
cdm.js:769 a1: 0
cdm.js:770 a2: -30
cdm.js:807 v: 30, 0, 0
cdm.js:746 P1: 4, P2: 3
cdm.js:747 v1: 30, 0, 0
cdm.js:748 v2: 0, 0, 0
cdm.js:769 a1: 30
cdm.js:770 a2: 0
cdm.js:807 v: -30, 0, 0
cdm.js:746 P1: 5, P2: 6
cdm.js:747 v1: 40, 0, 0
cdm.js:748 v2: -40, 0, 0
cdm.js:769 a1: 40
cdm.js:770 a2: -40
cdm.js:807 v: -80, 0, 0
cdm.js:746 P1: 6, P2: 5
cdm.js:747 v1: -40, 0, 0
cdm.js:748 v2: 40, 0, 0
cdm.js:769 a1: 40
cdm.js:770 a2: -40
cdm.js:807 v: 80, 0, 0
cdm.js:746 P1: 3, P2: 4
cdm.js:747 v1: 30, 0, 0
cdm.js:748 v2: 0, 0, 0
cdm.js:769 a1: -29.999999999999996
cdm.js:770 a2: 0
cdm.js:807 v: -29.999999999999993, 0, 0
cdm.js:746 P1: 4, P2: 3
cdm.js:747 v1: 0, 0, 0
cdm.js:748 v2: 30, 0, 0
cdm.js:769 a1: 0
cdm.js:770 a2: 29.999999999999996
cdm.js:807 v: 29.999999999999993, 0, 0
cdm.js:746 P1: 5, P2: 6
cdm.js:747 v1: -40, 0, 0
cdm.js:748 v2: 40, 0, 0
cdm.js:769 a1: 40
cdm.js:770 a2: -40
cdm.js:807 v: 80, 0, 0
cdm.js:746 P1: 6, P2: 5
cdm.js:747 v1: 40, 0, 0
cdm.js:748 v2: -40, 0, 0
cdm.js:769 a1: 40
cdm.js:770 a2: -40
cdm.js:807 v: -80, 0, 0
cdm.js:746 P1: 5, P2: 6
cdm.js:747 v1: 40, 0, 0
cdm.js:748 v2: -40, 0, 0
cdm.js:769 a1: 40
cdm.js:770 a2: -40
cdm.js:807 v: -80, 0, 0
cdm.js:746 P1: 6, P2: 5
cdm.js:747 v1: -40, 0, 0
cdm.js:748 v2: 40, 0, 0
cdm.js:769 a1: 40
cdm.js:770 a2: -40
cdm.js:807 v: 80, 0, 0
cdm.js:746 P1: 5, P2: 6
cdm.js:747 v1: -40, 0, 0
cdm.js:748 v2: 40, 0, 0
cdm.js:769 a1: 40
cdm.js:770 a2: -40
cdm.js:807 v: 80, 0, 0
cdm.js:746 P1: 6, P2: 5
cdm.js:747 v1: 40, 0, 0
cdm.js:748 v2: -40, 0, 0
cdm.js:769 a1: 40
cdm.js:770 a2: -40
cdm.js:807 v: -80, 0, 0
cdm.js:746 P1: 5, P2: 6
cdm.js:747 v1: 40, 0, 0
cdm.js:748 v2: -40, 0, 0
cdm.js:769 a1: 40
cdm.js:770 a2: -40
cdm.js:807 v: -80, 0, 0
cdm.js:746 P1: 6, P2: 5
cdm.js:747 v1: -40, 0, 0
cdm.js:748 v2: 40, 0, 0
cdm.js:769 a1: 40
cdm.js:770 a2: -40
cdm.js:807 v: 80, 0, 0
cdm.js:746 P1: 5, P2: 6
cdm.js:747 v1: -40, 0, 0
cdm.js:748 v2: 40, 0, 0
cdm.js:769 a1: 40
cdm.js:770 a2: -40
cdm.js:807 v: 80, 0, 0
cdm.js:746 P1: 6, P2: 5
cdm.js:747 v1: 40, 0, 0
cdm.js:748 v2: -40, 0, 0
cdm.js:769 a1: 40
cdm.js:770 a2: -40
cdm.js:807 v: -80, 0, 0
cdm.js:746 P1: 5, P2: 6
cdm.js:747 v1: 40, 0, 0
cdm.js:748 v2: -40, 0, 0
cdm.js:769 a1: 40
cdm.js:770 a2: -40
cdm.js:807 v: -80, 0, 0
cdm.js:746 P1: 6, P2: 5
cdm.js:747 v1: -40, 0, 0
cdm.js:748 v2: 40, 0, 0
cdm.js:769 a1: 40
cdm.js:770 a2: -40
cdm.js:807 v: 80, 0, 0
cdm.js:746 P1: 5, P2: 6
cdm.js:747 v1: -40, 0, 0
cdm.js:748 v2: 40, 0, 0
cdm.js:769 a1: 40
cdm.js:770 a2: -40
cdm.js:807 v: 80, 0, 0
cdm.js:746 P1: 6, P2: 5
cdm.js:747 v1: 40, 0, 0
cdm.js:748 v2: -40, 0, 0
cdm.js:769 a1: 40
cdm.js:770 a2: -40
cdm.js:807 v: -80, 0, 0
cdm.js:746 P1: 5, P2: 6
cdm.js:747 v1: 40, 0, 0
cdm.js:748 v2: -40, 0, 0
cdm.js:769 a1: 40
cdm.js:770 a2: -40
cdm.js:807 v: -80, 0, 0
cdm.js:746 P1: 6, P2: 5
cdm.js:747 v1: -40, 0, 0
cdm.js:748 v2: 40, 0, 0
cdm.js:769 a1: 40
cdm.js:770 a2: -40
cdm.js:807 v: 80, 0, 0
cdm.js:746 P1: 5, P2: 6
cdm.js:747 v1: -40, 0, 0
cdm.js:748 v2: 40, 0, 0
cdm.js:769 a1: -40
cdm.js:770 a2: 40
cdm.js:807 v: 80, 0, 0
cdm.js:746 P1: 6, P2: 5
cdm.js:747 v1: 40, 0, 0
cdm.js:748 v2: -40, 0, 0
cdm.js:769 a1: -40
cdm.js:770 a2: 40
cdm.js:807 v: -80, 0, 0
cdm.js:746 P1: 5, P2: 6
cdm.js:747 v1: 40, 0, 0
cdm.js:748 v2: -40, 0, 0
cdm.js:769 a1: 40
cdm.js:770 a2: -40
cdm.js:807 v: -80, 0, 0
cdm.js:746 P1: 6, P2: 5
cdm.js:747 v1: -40, 0, 0
cdm.js:748 v2: 40, 0, 0
cdm.js:769 a1: 40
cdm.js:770 a2: -40
cdm.js:807 v: 80, 0, 0
cdm.js:746 P1: 5, P2: 6
cdm.js:747 v1: -40, 0, 0
cdm.js:748 v2: 40, 0, 0
cdm.js:769 a1: -40
cdm.js:770 a2: 40
cdm.js:807 v: 80, 0, 0
cdm.js:746 P1: 6, P2: 5
cdm.js:747 v1: 40, 0, 0
cdm.js:748 v2: -40, 0, 0
cdm.js:769 a1: -40
cdm.js:770 a2: 40
cdm.js:807 v: -80, 0, 0
cdm.js:746 P1: 5, P2: 6
cdm.js:747 v1: 40, 0, 0
cdm.js:748 v2: -40, 0, 0
cdm.js:769 a1: 40
cdm.js:770 a2: -40
cdm.js:807 v: -80, 0, 0
cdm.js:746 P1: 6, P2: 5
cdm.js:747 v1: -40, 0, 0
cdm.js:748 v2: 40, 0, 0
cdm.js:769 a1: 40
cdm.js:770 a2: -40
cdm.js:807 v: 80, 0, 0
cdm.js:746 P1: 5, P2: 6
cdm.js:747 v1: -40, 0, 0
cdm.js:748 v2: 40, 0, 0
cdm.js:769 a1: -40
cdm.js:770 a2: 40
cdm.js:807 v: 80, 0, 0
cdm.js:746 P1: 6, P2: 5
cdm.js:747 v1: 40, 0, 0
cdm.js:748 v2: -40, 0, 0
cdm.js:769 a1: -40
cdm.js:770 a2: 40
cdm.js:807 v: -80, 0, 0
cdm.js:746 P1: 5, P2: 6
cdm.js:747 v1: 40, 0, 0
cdm.js:748 v2: -40, 0, 0
cdm.js:769 a1: 40
cdm.js:770 a2: -40
cdm.js:807 v: -80, 0, 0
cdm.js:746 P1: 6, P2: 5
cdm.js:747 v1: -40, 0, 0
cdm.js:748 v2: 40, 0, 0
cdm.js:769 a1: 40
cdm.js:770 a2: -40
cdm.js:807 v: 80, 0, 0
cdm.js:746 P1: 5, P2: 6
cdm.js:747 v1: -40, 0, 0
cdm.js:748 v2: 40, 0, 0
cdm.js:769 a1: -39.99999999999999
cdm.js:770 a2: 39.99999999999999
cdm.js:807 v: 79.99999999999997, 0, 0
cdm.js:746 P1: 6, P2: 5
cdm.js:747 v1: 40, 0, 0
cdm.js:748 v2: -40, 0, 0
cdm.js:769 a1: -39.99999999999999
cdm.js:770 a2: 39.99999999999999
cdm.js:807 v: -79.99999999999997, 0, 0
cdm.js:746 P1: 5, P2: 6
cdm.js:747 v1: 40, 0, 0
cdm.js:748 v2: -40, 0, 0
cdm.js:769 a1: 40
cdm.js:770 a2: -40
cdm.js:807 v: -80, 0, 0
cdm.js:746 P1: 6, P2: 5
cdm.js:747 v1: -40, 0, 0
cdm.js:748 v2: 40, 0, 0
cdm.js:769 a1: 40
cdm.js:770 a2: -40
cdm.js:807 v: 80, 0, 0
cdm.js:746 P1: 5, P2: 6
cdm.js:747 v1: -40, 0, 0
cdm.js:748 v2: 40, 0, 0
cdm.js:769 a1: -40
cdm.js:770 a2: 40
cdm.js:807 v: 80, 0, 0
cdm.js:746 P1: 6, P2: 5
cdm.js:747 v1: 40, 0, 0
cdm.js:748 v2: -40, 0, 0
cdm.js:769 a1: -40
cdm.js:770 a2: 40
cdm.js:807 v: -80, 0, 0
cdm.js:746 P1: 5, P2: 6
cdm.js:747 v1: 40, 0, 0
cdm.js:748 v2: -40, 0, 0
cdm.js:769 a1: 40
cdm.js:770 a2: -40
cdm.js:807 v: -80, 0, 0
cdm.js:746 P1: 6, P2: 5
cdm.js:747 v1: -40, 0, 0
cdm.js:748 v2: 40, 0, 0
cdm.js:769 a1: 40
cdm.js:770 a2: -40
cdm.js:807 v: 80, 0, 0
cdm.js:746 P1: 5, P2: 6
cdm.js:747 v1: -40, 0, 0
cdm.js:748 v2: 40, 0, 0
cdm.js:769 a1: -40
cdm.js:770 a2: 40
cdm.js:807 v: 80, 0, 0
cdm.js:746 P1: 6, P2: 5
cdm.js:747 v1: 40, 0, 0
cdm.js:748 v2: -40, 0, 0
cdm.js:769 a1: -40
cdm.js:770 a2: 40
cdm.js:807 v: -80, 0, 0
cdm.js:746 P1: 5, P2: 6
cdm.js:747 v1: 40, 0, 0
cdm.js:748 v2: -40, 0, 0
cdm.js:769 a1: 40
cdm.js:770 a2: -40
cdm.js:807 v: -80, 0, 0
cdm.js:746 P1: 6, P2: 5
cdm.js:747 v1: -40, 0, 0
cdm.js:748 v2: 40, 0, 0
cdm.js:769 a1: 40
cdm.js:770 a2: -40
cdm.js:807 v: 80, 0, 0
cdm.js:746 P1: 5, P2: 6
cdm.js:747 v1: -40, 0, 0
cdm.js:748 v2: 40, 0, 0
cdm.js:769 a1: -40
cdm.js:770 a2: 40
cdm.js:807 v: 80, 0, 0
cdm.js:746 P1: 6, P2: 5
cdm.js:747 v1: 40, 0, 0
cdm.js:748 v2: -40, 0, 0
cdm.js:769 a1: -40
cdm.js:770 a2: 40
cdm.js:807 v: -80, 0, 0
cdm.js:746 P1: 5, P2: 6
cdm.js:747 v1: 40, 0, 0
cdm.js:748 v2: -40, 0, 0
cdm.js:769 a1: 40
cdm.js:770 a2: -40
cdm.js:807 v: -80, 0, 0
cdm.js:746 P1: 6, P2: 5
cdm.js:747 v1: -40, 0, 0
cdm.js:748 v2: 40, 0, 0
cdm.js:769 a1: 40
cdm.js:770 a2: -40
cdm.js:807 v: 80, 0, 0
cdm.js:746 P1: 5, P2: 6
cdm.js:747 v1: -40, 0, 0
cdm.js:748 v2: 40, 0, 0
cdm.js:769 a1: -40
cdm.js:770 a2: 40
cdm.js:807 v: 80, 0, 0
cdm.js:746 P1: 6, P2: 5
cdm.js:747 v1: 40, 0, 0
cdm.js:748 v2: -40, 0, 0
cdm.js:769 a1: -40
cdm.js:770 a2: 40
cdm.js:807 v: -80, 0, 0
cdm.js:746 P1: 5, P2: 6
cdm.js:747 v1: 40, 0, 0
cdm.js:748 v2: -40, 0, 0
cdm.js:769 a1: 40
cdm.js:770 a2: -40
cdm.js:807 v: -80, 0, 0
cdm.js:746 P1: 6, P2: 5
cdm.js:747 v1: -40, 0, 0
cdm.js:748 v2: 40, 0, 0
cdm.js:769 a1: 40
cdm.js:770 a2: -40
cdm.js:807 v: 80, 0, 0
cdm.js:746 P1: 5, P2: 6
cdm.js:747 v1: -40, 0, 0
cdm.js:748 v2: 40, 0, 0
cdm.js:769 a1: -40
cdm.js:770 a2: 40
cdm.js:807 v: 80, 0, 0
cdm.js:746 P1: 6, P2: 5
cdm.js:747 v1: 40, 0, 0
cdm.js:748 v2: -40, 0, 0
cdm.js:769 a1: -40
cdm.js:770 a2: 40
cdm.js:807 v: -80, 0, 0
cdm.js:746 P1: 5, P2: 6
cdm.js:747 v1: 40, 0, 0
cdm.js:748 v2: -40, 0, 0
cdm.js:769 a1: 39.99999999999999
cdm.js:770 a2: -39.99999999999999
cdm.js:807 v: -79.99999999999997, 0, 0
cdm.js:746 P1: 6, P2: 5
cdm.js:747 v1: -40, 0, 0
cdm.js:748 v2: 40, 0, 0
cdm.js:769 a1: 39.99999999999999
cdm.js:770 a2: -39.99999999999999
cdm.js:807 v: 79.99999999999997, 0, 0
cdm.js:746 P1: 5, P2: 6
cdm.js:747 v1: -40, 0, 0
cdm.js:748 v2: 40, 0, 0
cdm.js:769 a1: -40
cdm.js:770 a2: 40
cdm.js:807 v: 80, 0, 0
cdm.js:746 P1: 6, P2: 5
cdm.js:747 v1: 40, 0, 0
cdm.js:748 v2: -40, 0, 0
cdm.js:769 a1: -40
cdm.js:770 a2: 40
cdm.js:807 v: -80, 0, 0
cdm.js:746 P1: 5, P2: 6
cdm.js:747 v1: 40, 0, 0
cdm.js:748 v2: -40, 0, 0
cdm.js:769 a1: 40
cdm.js:770 a2: -40
cdm.js:807 v: -80, 0, 0
cdm.js:746 P1: 6, P2: 5
cdm.js:747 v1: -40, 0, 0
cdm.js:748 v2: 40, 0, 0
cdm.js:769 a1: 40
cdm.js:770 a2: -40
cdm.js:807 v: 80, 0, 0
cdm.js:746 P1: 5, P2: 6
cdm.js:747 v1: -40, 0, 0
cdm.js:748 v2: 40, 0, 0
cdm.js:769 a1: -40
cdm.js:770 a2: 40
cdm.js:807 v: 80, 0, 0
cdm.js:746 P1: 6, P2: 5
cdm.js:747 v1: 40, 0, 0
cdm.js:748 v2: -40, 0, 0
cdm.js:769 a1: -40
cdm.js:770 a2: 40
cdm.js:807 v: -80, 0, 0
cdm.js:746 P1: 5, P2: 6
cdm.js:747 v1: 40, 0, 0
cdm.js:748 v2: -40, 0, 0
cdm.js:769 a1: 40
cdm.js:770 a2: -40
cdm.js:807 v: -80, 0, 0
cdm.js:746 P1: 6, P2: 5
cdm.js:747 v1: -40, 0, 0
cdm.js:748 v2: 40, 0, 0
cdm.js:769 a1: 40
cdm.js:770 a2: -40
cdm.js:807 v: 80, 0, 0
cdm.js:746 P1: 5, P2: 6
cdm.js:747 v1: -40, 0, 0
cdm.js:748 v2: 40, 0, 0
cdm.js:769 a1: -40
cdm.js:770 a2: 40
cdm.js:807 v: 80, 0, 0
cdm.js:746 P1: 6, P2: 5
cdm.js:747 v1: 40, 0, 0
cdm.js:748 v2: -40, 0, 0
cdm.js:769 a1: -40
cdm.js:770 a2: 40
cdm.js:807 v: -80, 0, 0
cdm.js:746 P1: 5, P2: 6
cdm.js:747 v1: 40, 0, 0
cdm.js:748 v2: -40, 0, 0
cdm.js:769 a1: 39.99999999999999
cdm.js:770 a2: -39.99999999999999
cdm.js:807 v: -79.99999999999997, 0, 0
cdm.js:746 P1: 6, P2: 5
cdm.js:747 v1: -40, 0, 0
cdm.js:748 v2: 40, 0, 0
cdm.js:769 a1: 39.99999999999999
cdm.js:770 a2: -39.99999999999999
cdm.js:807 v: 79.99999999999997, 0, 0
cdm.js:746 P1: 5, P2: 6
cdm.js:747 v1: -40, 0, 0
cdm.js:748 v2: 40, 0, 0
cdm.js:769 a1: -40
cdm.js:770 a2: 40
cdm.js:807 v: 80, 0, 0
cdm.js:746 P1: 6, P2: 5
cdm.js:747 v1: 40, 0, 0
cdm.js:748 v2: -40, 0, 0
cdm.js:769 a1: -40
cdm.js:770 a2: 40
cdm.js:807 v: -80, 0, 0
cdm.js:746 P1: 5, P2: 6
cdm.js:747 v1: 40, 0, 0
cdm.js:748 v2: -40, 0, 0
cdm.js:769 a1: 39.99999999999999
cdm.js:770 a2: -39.99999999999999
cdm.js:807 v: -79.99999999999997, 0, 0
cdm.js:746 P1: 6, P2: 5
cdm.js:747 v1: -40, 0, 0
cdm.js:748 v2: 40, 0, 0
cdm.js:769 a1: 39.99999999999999
cdm.js:770 a2: -39.99999999999999
cdm.js:807 v: 79.99999999999997, 0, 0
cdm.js:746 P1: 5, P2: 6
cdm.js:747 v1: -40, 0, 0
cdm.js:748 v2: 40, 0, 0
cdm.js:769 a1: -39.99999999999999
cdm.js:770 a2: 39.99999999999999
cdm.js:807 v: 79.99999999999997, 0, 0
cdm.js:746 P1: 6, P2: 5
cdm.js:747 v1: 40, 0, 0
cdm.js:748 v2: -40, 0, 0
cdm.js:769 a1: -39.99999999999999
cdm.js:770 a2: 39.99999999999999
cdm.js:807 v: -79.99999999999997, 0, 0
cdm.js:746 P1: 5, P2: 6
cdm.js:747 v1: 40, 0, 0
cdm.js:748 v2: -40, 0, 0
cdm.js:769 a1: 40
cdm.js:770 a2: -40
cdm.js:807 v: -80, 0, 0
cdm.js:746 P1: 6, P2: 5
cdm.js:747 v1: -40, 0, 0
cdm.js:748 v2: 40, 0, 0
cdm.js:769 a1: 40
cdm.js:770 a2: -40
cdm.js:807 v: 80, 0, 0
cdm.js:746 P1: 5, P2: 6
cdm.js:747 v1: -40, 0, 0
cdm.js:748 v2: 40, 0, 0
cdm.js:769 a1: -40
cdm.js:770 a2: 40
cdm.js:807 v: 80, 0, 0
cdm.js:746 P1: 6, P2: 5
cdm.js:747 v1: 40, 0, 0
cdm.js:748 v2: -40, 0, 0
cdm.js:769 a1: -40
cdm.js:770 a2: 40
cdm.js:807 v: -80, 0, 0
cdm.js:746 P1: 5, P2: 6
cdm.js:747 v1: 40, 0, 0
cdm.js:748 v2: -40, 0, 0
cdm.js:769 a1: 39.99999999999999
cdm.js:770 a2: -39.99999999999999
cdm.js:807 v: -79.99999999999997, 0, 0
cdm.js:746 P1: 6, P2: 5
cdm.js:747 v1: -40, 0, 0
cdm.js:748 v2: 40, 0, 0
cdm.js:769 a1: 39.99999999999999
cdm.js:770 a2: -39.99999999999999
cdm.js:807 v: 79.99999999999997, 0, 0
cdm.js:746 P1: 5, P2: 6
cdm.js:747 v1: -40, 0, 0
cdm.js:748 v2: 40, 0, 0
cdm.js:769 a1: -40
cdm.js:770 a2: 40
cdm.js:807 v: 80, 0, 0
cdm.js:746 P1: 6, P2: 5
cdm.js:747 v1: 40, 0, 0
cdm.js:748 v2: -40, 0, 0
cdm.js:769 a1: -40
cdm.js:770 a2: 40
cdm.js:807 v: -80, 0, 0
cdm.js:746 P1: 5, P2: 6
cdm.js:747 v1: 40, 0, 0
cdm.js:748 v2: -40, 0, 0
cdm.js:769 a1: 40
cdm.js:770 a2: -40
cdm.js:807 v: -80, 0, 0
cdm.js:746 P1: 6, P2: 5
cdm.js:747 v1: -40, 0, 0
cdm.js:748 v2: 40, 0, 0
cdm.js:769 a1: 40
cdm.js:770 a2: -40
cdm.js:807 v: 80, 0, 0
cdm.js:746 P1: 5, P2: 6
cdm.js:747 v1: -40, 0, 0
cdm.js:748 v2: 40, 0, 0
cdm.js:769 a1: -40
cdm.js:770 a2: 40
cdm.js:807 v: 80, 0, 0
cdm.js:746 P1: 6, P2: 5
cdm.js:747 v1: 40, 0, 0
cdm.js:748 v2: -40, 0, 0
cdm.js:769 a1: -40
cdm.js:770 a2: 40
cdm.js:807 v: -80, 0, 0
cdm.js:746 P1: 5, P2: 7
cdm.js:747 v1: 40, 0, 0
cdm.js:748 v2: 0, 0, 0
cdm.js:769 a1: -39.99999999999999
cdm.js:770 a2: 0
cdm.js:807 v: -39.999999999999986, 0, 0
cdm.js:746 P1: 7, P2: 5
cdm.js:747 v1: 0, 0, 0
cdm.js:748 v2: 40, 0, 0
cdm.js:769 a1: 0
cdm.js:770 a2: 39.99999999999999
cdm.js:807 v: 39.999999999999986, 0, 0
cdm.js:746 P1: 7, P2: 8
cdm.js:747 v1: 40, 0, 0
cdm.js:748 v2: 0, 0, 0
cdm.js:769 a1: -40
cdm.js:770 a2: 0
cdm.js:807 v: -40, 0, 0
cdm.js:746 P1: 8, P2: 7
cdm.js:747 v1: 0, 0, 0
cdm.js:748 v2: 40, 0, 0
cdm.js:769 a1: 0
cdm.js:770 a2: 40
cdm.js:807 v: 40, 0, 0
cdm.js:746 P1: 7, P2: 8
cdm.js:747 v1: 0, 0, 0
cdm.js:748 v2: 40, 0, 0
cdm.js:769 a1: 0
cdm.js:770 a2: -40
cdm.js:807 v: 40, 0, 0
cdm.js:746 P1: 8, P2: 7
cdm.js:747 v1: 40, 0, 0
cdm.js:748 v2: 0, 0, 0
cdm.js:769 a1: 40
cdm.js:770 a2: 0
cdm.js:807 v: -40, 0, 0
cdm.js:746 P1: 7, P2: 8
cdm.js:747 v1: 40, 0, 0
cdm.js:748 v2: 0, 0, 0
cdm.js:769 a1: -40
cdm.js:770 a2: 0
cdm.js:807 v: -40, 0, 0
cdm.js:746 P1: 8, P2: 7
cdm.js:747 v1: 0, 0, 0
cdm.js:748 v2: 40, 0, 0
cdm.js:769 a1: 0
cdm.js:770 a2: 40
cdm.js:807 v: 40, 0, 0
I hope you'll be requesting position locations next?
Thanks for that Sourcetree idea, I'll look into it.
.
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
I am thinking about changing the way these functions are called. They are currently implemented to look for a collision that has just occurred but I want to change it to look for collisions that are about to occur.
Unfortunately, that is a bit difficult. The problem is that I have specified velocities in world units, such as m/s (the seconds is what matters), and I adjust the actual velocity used for a given frame by using the amount of time since the last frame. So if 1/60th of a second has past since the last frame, then I use 1/60th of the velocity. This has the advantage of using the correct amount of velocity for the given time (even if it was 1/45th of a second or 1/73.563). To look for a collision that might happen, I need to know the actual velocity being used, not the real world value, because I need to project into the future to see what will happen.
I just need to find a way around that. I will probably need to pass in the frame time to these methods to do so.
There probably isn't much point to you debugging this issue. Of course, it's a great exercise in finding problems and it really makes you figure out what the code is really doing and why, so you can continue if you want.
I really appreciate the effort you have put in. Also for pushing when you weren't happy with my responses. I haven't been thinking clearly, as my conflicting posts show, so it has been a saving-grace that you haven't just accepted whatever I say or just sat back and waited for me to fix it. Even if I am correct, you need to understand why I am correct and the same thing applies to me. We aren't just building an application, the real important stuff is transferring information and skills, and you have not let yourself down by being a passive student.
Unfortunately, that is a bit difficult. The problem is that I have specified velocities in world units, such as m/s (the seconds is what matters), and I adjust the actual velocity used for a given frame by using the amount of time since the last frame. So if 1/60th of a second has past since the last frame, then I use 1/60th of the velocity. This has the advantage of using the correct amount of velocity for the given time (even if it was 1/45th of a second or 1/73.563). To look for a collision that might happen, I need to know the actual velocity being used, not the real world value, because I need to project into the future to see what will happen.
I just need to find a way around that. I will probably need to pass in the frame time to these methods to do so.
There probably isn't much point to you debugging this issue. Of course, it's a great exercise in finding problems and it really makes you figure out what the code is really doing and why, so you can continue if you want.
I really appreciate the effort you have put in. Also for pushing when you weren't happy with my responses. I haven't been thinking clearly, as my conflicting posts show, so it has been a saving-grace that you haven't just accepted whatever I say or just sat back and waited for me to fix it. Even if I am correct, you need to understand why I am correct and the same thing applies to me. We aren't just building an application, the real important stuff is transferring information and skills, and you have not let yourself down by being a passive student.
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
.
I saw that flag in Sourcetree. Click on it and it says- Tell us what you think. So I ignored it since. This time I saw that yes, a sourcetree update was available, so I did. After restarting I tried to Push and experienced the same error as before. No joy.
I repeat, this is a great learning opportunity. Frame breaking isn't that difficult, but I'm nowhere near understanding how you've got this application wired else I'd have given you even more grief. I need to study it, even if you don't end up using it. As far as ideas go, I don't like the particle charge emission range = 10. You might consider a charge range limit, based on an angular limit - like the moon and the sun are apparently the same size. Monitor distance^2 just within smaller or closer groups. Or what about gravity? Just messin' with ya.
I admit, part of my effort is to motivate you. You've held up easily, doing a huge amount of work I'm barely able to appreciate. Relax and get your thoughts in order.
.
I saw that flag in Sourcetree. Click on it and it says- Tell us what you think. So I ignored it since. This time I saw that yes, a sourcetree update was available, so I did. After restarting I tried to Push and experienced the same error as before. No joy.
I repeat, this is a great learning opportunity. Frame breaking isn't that difficult, but I'm nowhere near understanding how you've got this application wired else I'd have given you even more grief. I need to study it, even if you don't end up using it. As far as ideas go, I don't like the particle charge emission range = 10. You might consider a charge range limit, based on an angular limit - like the moon and the sun are apparently the same size. Monitor distance^2 just within smaller or closer groups. Or what about gravity? Just messin' with ya.
I admit, part of my effort is to motivate you. You've held up easily, doing a huge amount of work I'm barely able to appreciate. Relax and get your thoughts in order.
.
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
I did exactly the same thing with that orange flag, until a colleague pointed out that it had an update in it.
After updating SourceTree, go to the BitBucket website and login there. Then restart SourceTree and see if you can push. Also, re-enter your password to SourceTree, just in case it has lost it (Tools -> Options -> Authentication tab).
I agree about that emission range. It is a temporary approximation and will be replaced by a 1/r^4 type calculation. Some of the charge interaction code will need to change for the same reason. It is just a rough approximation at the moment and can be made better now that we know the rest of the algorithm works. The current charge code is a linear progression as you move further away from the emitter, which is clearly not right. I was focused on the equator to pole relationship of charge emission and how to process that, so the actual charge calculations were just rough calculations to get something close to what I wanted.
I did some research into the proper math and ran into a problem, which also applies to gravity at this level. Miles' work on that stuff is based on planets and moons. We are working with protons and other tiny particles. Miles takes some time to explain that the 1/r^2 relationship of gravity is actually an outcome of time/distance separation. It takes more time for the charge from the Sun to reach Saturn than it does the Earth, therefore at the exact same moment, Saturn sees older charge (which came from a smaller Sun) than the Earth does. We do not have such time/distance separations and I need to know how to remove such assumptions from the equations.
After updating SourceTree, go to the BitBucket website and login there. Then restart SourceTree and see if you can push. Also, re-enter your password to SourceTree, just in case it has lost it (Tools -> Options -> Authentication tab).
I agree about that emission range. It is a temporary approximation and will be replaced by a 1/r^4 type calculation. Some of the charge interaction code will need to change for the same reason. It is just a rough approximation at the moment and can be made better now that we know the rest of the algorithm works. The current charge code is a linear progression as you move further away from the emitter, which is clearly not right. I was focused on the equator to pole relationship of charge emission and how to process that, so the actual charge calculations were just rough calculations to get something close to what I wanted.
I did some research into the proper math and ran into a problem, which also applies to gravity at this level. Miles' work on that stuff is based on planets and moons. We are working with protons and other tiny particles. Miles takes some time to explain that the 1/r^2 relationship of gravity is actually an outcome of time/distance separation. It takes more time for the charge from the Sun to reach Saturn than it does the Earth, therefore at the exact same moment, Saturn sees older charge (which came from a smaller Sun) than the Earth does. We do not have such time/distance separations and I need to know how to remove such assumptions from the equations.
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
.
Hey Nevyn, you may have noticed I Pushed to Bitbucket. Customer Service recommended I install a windows bug fix Git Credential Manager for Windows 1.17.0 and remove all bitbucket credentials from my Windows Credential Manager. It worked!
I'm looking at separation distances for the collision errors and was aghast at the overlap distances - for non-error collisions too. The easiest fix may be improved collision detection. I wonder if I could import the console output into excel or R and do this sort of thing automatically.
Tracking the time necessary for separation distances fixes the scale of particle interaction. I agree, a larger scale requires more time. I would assume we have a constant scale for any given particle configuration.Whether we simulate proton or planet, we are adjusting time differentials to account for the motions that we are creating. Sorry if I'm missing the gist.
.
Hey Nevyn, you may have noticed I Pushed to Bitbucket. Customer Service recommended I install a windows bug fix Git Credential Manager for Windows 1.17.0 and remove all bitbucket credentials from my Windows Credential Manager. It worked!
I'm looking at separation distances for the collision errors and was aghast at the overlap distances - for non-error collisions too. The easiest fix may be improved collision detection. I wonder if I could import the console output into excel or R and do this sort of thing automatically.
Tracking the time necessary for separation distances fixes the scale of particle interaction. I agree, a larger scale requires more time. I would assume we have a constant scale for any given particle configuration.Whether we simulate proton or planet, we are adjusting time differentials to account for the motions that we are creating. Sorry if I'm missing the gist.
.
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
Yeah, that's basically it. A planet is a long distance from its star, so it takes time for the charge to reach that planet, even at the extreme speed that charge moves at. But it takes virtually no time for a charge photon to move from one proton to another if they are close enough to be interacting. So we don't need to include the distance separation in that way.
I have been playing with numbers again, and I think I see a way to calculate the charge strengths we want. Instead of a 1/r^4 calculation, it will be a 1/r^3 based equation. That is because it only uses the reduction in volume associated with that distance and not the time, which would bring in the distance again and give us r^4.
Volume of a Sphere: (4*Pi*r^3)/3
A radius of 1 represents the boundary of the emitter. That is the highest charge strength or charge density, which ever way you want to look at it.
A radius of 10 represents the furthest point away from the emitter in this dataset. Note that the radius is from the center of the emitter, not the boundary.
What we are looking at here is how and why the charge diminishes with distance. The particle only emits a certain amount of charge, at any given time or over some set time period, and that is constant (for our purposes here, it can change if the ambient field density changes but would still be a constant for us as we are working relative to the ambient field). So as that charge moves away from the particle, it inhabits a larger volume. The same amount of charge in a greater volume means less density.
So we want to look at how that volume changes as we use a greater radius. You can perform a little bit of calculus on it and find that the 3rd derivative, which is the constant derivative, has a value of 25.1327412287. That doesn't really tell us anything though. So let's take some ratios and see what it tells us.
Firstly, we will divide each volume by the first volume to see how many of the initial volume can fit into the larger volumes. In essence, this is making all volumes relative to the first volume.
A few of those numbers look familiar, and a quick analysis shows that each value is r^3. That wasn't too surprising, since we are using an r^3 equation, but I thought it worth showing as a stepping stone to the next part of this analysis.
That number tells us how much charge we could fit into each volume if we wanted to keep the charge density constant. But we don't want to keep the density constant, we want to keep the amount of charge constant and allow the density to change. So we are looking for the inverse of that value. We want to know how a given amount of charge will fit into a larger volume so we want to divide the first volume by each other volume.
Now we have a number that means something to us. We can take that number and multiply it by the charge strength at the particle boundary and get the charge strength at that volume. We will actually use the 1/r^3 equation to find the value for any radius. I did think about using a lookup table like this but the equation isn't that expensive so it isn't worth it. Precision is more important.
So my initial guess of the maximum charge emission range being 10 radii is pretty good. At that distance, the charge strength should be 1000 times less than at the particle boundary. Is it a coincidence that the Earth's chargepause, which sets the magnetopause and others, is also at 11 to 12 radii? I think not. In fact, I know not because it is the same reasons for both. If I had realised that when I created the constant in the code I would have used 11 or 12 instead.
So now we have an equation to calculate the charge at a given distance: C(d) = C(1)/d^3
Please note that I am using an equation within an equation. C is an equation to calculate the charge density or strength given a radius. So that equation explicitly states: The charge density at d is equal to the charge density at 1 divided by d^3. The charge density equation could be as simple as mass times volume, maybe mass times surface area or it could be more convoluted.
This is a quantum equation. It does not apply to macro-scale numbers. We are ignoring time because the particles are close enough to do so, stars, planets, and moons are not, so it becomes a d^4 equation instead.
I have been playing with numbers again, and I think I see a way to calculate the charge strengths we want. Instead of a 1/r^4 calculation, it will be a 1/r^3 based equation. That is because it only uses the reduction in volume associated with that distance and not the time, which would bring in the distance again and give us r^4.
Analysis of Volume
Volume of a Sphere: (4*Pi*r^3)/3
| Radius | Volume |
| 1 | 4.1887902048 |
| 2 | 33.5103216383 |
| 3 | 113.0973355292 |
| 4 | 268.0825731063 |
| 5 | 523.5987755983 |
| 6 | 904.7786842339 |
| 7 | 1436.7550402417 |
| 8 | 2144.6605848506 |
| 9 | 3053.6280592893 |
| 10 | 4188.7902047864 |
A radius of 1 represents the boundary of the emitter. That is the highest charge strength or charge density, which ever way you want to look at it.
A radius of 10 represents the furthest point away from the emitter in this dataset. Note that the radius is from the center of the emitter, not the boundary.
What we are looking at here is how and why the charge diminishes with distance. The particle only emits a certain amount of charge, at any given time or over some set time period, and that is constant (for our purposes here, it can change if the ambient field density changes but would still be a constant for us as we are working relative to the ambient field). So as that charge moves away from the particle, it inhabits a larger volume. The same amount of charge in a greater volume means less density.
So we want to look at how that volume changes as we use a greater radius. You can perform a little bit of calculus on it and find that the 3rd derivative, which is the constant derivative, has a value of 25.1327412287. That doesn't really tell us anything though. So let's take some ratios and see what it tells us.
Firstly, we will divide each volume by the first volume to see how many of the initial volume can fit into the larger volumes. In essence, this is making all volumes relative to the first volume.
| Radius | Volume | V(n) / V(1) |
| 1 | 4.1887902048 | 1 |
| 2 | 33.5103216383 | 8 |
| 3 | 113.0973355292 | 27 |
| 4 | 268.0825731063 | 64 |
| 5 | 523.5987755983 | 125 |
| 6 | 904.7786842339 | 216 |
| 7 | 1436.7550402417 | 343 |
| 8 | 2144.6605848506 | 512 |
| 9 | 3053.6280592893 | 729 |
| 10 | 4188.7902047864 | 1000 |
A few of those numbers look familiar, and a quick analysis shows that each value is r^3. That wasn't too surprising, since we are using an r^3 equation, but I thought it worth showing as a stepping stone to the next part of this analysis.
That number tells us how much charge we could fit into each volume if we wanted to keep the charge density constant. But we don't want to keep the density constant, we want to keep the amount of charge constant and allow the density to change. So we are looking for the inverse of that value. We want to know how a given amount of charge will fit into a larger volume so we want to divide the first volume by each other volume.
| Radius | Volume | V(n) / V(1) | V(1) / V(n) |
| 1 | 4.1887902048 | 1 | 1 |
| 2 | 33.5103216383 | 8 | 0.125 |
| 3 | 113.0973355292 | 27 | 0.037037037 |
| 4 | 268.0825731063 | 64 | 0.015625 |
| 5 | 523.5987755983 | 125 | 0.008 |
| 6 | 904.7786842339 | 216 | 0.0046296296 |
| 7 | 1436.7550402417 | 343 | 0.0029154519 |
| 8 | 2144.6605848506 | 512 | 0.001953125 |
| 9 | 3053.6280592893 | 729 | 0.0013717421 |
| 10 | 4188.7902047864 | 1000 | 0.001 |
Now we have a number that means something to us. We can take that number and multiply it by the charge strength at the particle boundary and get the charge strength at that volume. We will actually use the 1/r^3 equation to find the value for any radius. I did think about using a lookup table like this but the equation isn't that expensive so it isn't worth it. Precision is more important.
So my initial guess of the maximum charge emission range being 10 radii is pretty good. At that distance, the charge strength should be 1000 times less than at the particle boundary. Is it a coincidence that the Earth's chargepause, which sets the magnetopause and others, is also at 11 to 12 radii? I think not. In fact, I know not because it is the same reasons for both. If I had realised that when I created the constant in the code I would have used 11 or 12 instead.
So now we have an equation to calculate the charge at a given distance: C(d) = C(1)/d^3
Please note that I am using an equation within an equation. C is an equation to calculate the charge density or strength given a radius. So that equation explicitly states: The charge density at d is equal to the charge density at 1 divided by d^3. The charge density equation could be as simple as mass times volume, maybe mass times surface area or it could be more convoluted.
This is a quantum equation. It does not apply to macro-scale numbers. We are ignoring time because the particles are close enough to do so, stars, planets, and moons are not, so it becomes a d^4 equation instead.
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
I haven't thought this too far through yet, and I might be shooting my mouth off before I see it clearly enough, but I am hesitantly going to say that I don't think the macro equation should be an r^4 equation either. I think that I have the correct equation above.
It needs to be changed for use in the macro setting, though. We need to include the change in size of the emitter. Since the receiver is so far away, the charge that it receives was emitted at a time in the past. Using expansion theory, this means that the radius of the emitter was smaller when it emitted that charge. Well, my equation has a radius for the emitter right there. So let's use it for this purpose and see what happens.
C(d) = C(1)/d^3
That tells us the reduction in charge density based on volume only. The radius of the emitter is used in 2 places, although only one of them actually represents the emitter radius.
The d variable is used to represent the distance of the receiver from the emitter. It should be the distance of the point of measurement from the center of the emitter. This is likely to be the boundary of the receiver from the center of the emitter.
The other place it is used is as the number 1. In this case, it represents the radius of the emitter. Before, we only needed the number 1 as everything was relative and based on 1. Now, we want to change that value so we make it a variable. Let's call it r, for radius of the emitter.
C(d) = C(r)/d^3
Now we just need to know what r was when the charge was emitted. To find that, we need the distance it has traveled, which is d, since we know that it had a velocity of c, then we can determine how long it took that photon to travel to this point.
v = d/t -> vt = d -> t = d/v
v = c = 300, 000, 000m/s
t = d/c
Now we need to know how much a particle expands, per unit time, or unit time squared if it is an acceleration. Unfortunately, I don't know what that is. I don't even have a good guess. Maybe we can tease it out but I'll use a placeholder here instead. I'll create another equation for it and we can fill it in later.
Let R(n) be a function that calculates the radius of a sphere, given a value, n, that represents the time difference. When n=0, the current radius is returned. When n>0, a future radius is returned with n being the number of seconds into the future. When n<0, a past radius is returned with (the absolute value of) n being the number of seconds into the past.
Therefore, putting it back into our equation, we get:
C(d) = C( R(-d/c) )/d^3
That is a general equation that can be used at the micro or macro scale, but more useful at the macro. Maybe you could call it a relativistic equation, since it takes Relativity into account. It does contain 2 other equations, or functions, that need to be provided in order to find the actual equation.
Not a bad days work, eh?
It needs to be changed for use in the macro setting, though. We need to include the change in size of the emitter. Since the receiver is so far away, the charge that it receives was emitted at a time in the past. Using expansion theory, this means that the radius of the emitter was smaller when it emitted that charge. Well, my equation has a radius for the emitter right there. So let's use it for this purpose and see what happens.
C(d) = C(1)/d^3
That tells us the reduction in charge density based on volume only. The radius of the emitter is used in 2 places, although only one of them actually represents the emitter radius.
The d variable is used to represent the distance of the receiver from the emitter. It should be the distance of the point of measurement from the center of the emitter. This is likely to be the boundary of the receiver from the center of the emitter.
The other place it is used is as the number 1. In this case, it represents the radius of the emitter. Before, we only needed the number 1 as everything was relative and based on 1. Now, we want to change that value so we make it a variable. Let's call it r, for radius of the emitter.
C(d) = C(r)/d^3
Now we just need to know what r was when the charge was emitted. To find that, we need the distance it has traveled, which is d, since we know that it had a velocity of c, then we can determine how long it took that photon to travel to this point.
v = d/t -> vt = d -> t = d/v
v = c = 300, 000, 000m/s
t = d/c
Now we need to know how much a particle expands, per unit time, or unit time squared if it is an acceleration. Unfortunately, I don't know what that is. I don't even have a good guess. Maybe we can tease it out but I'll use a placeholder here instead. I'll create another equation for it and we can fill it in later.
Let R(n) be a function that calculates the radius of a sphere, given a value, n, that represents the time difference. When n=0, the current radius is returned. When n>0, a future radius is returned with n being the number of seconds into the future. When n<0, a past radius is returned with (the absolute value of) n being the number of seconds into the past.
Therefore, putting it back into our equation, we get:
C(d) = C( R(-d/c) )/d^3
That is a general equation that can be used at the micro or macro scale, but more useful at the macro. Maybe you could call it a relativistic equation, since it takes Relativity into account. It does contain 2 other equations, or functions, that need to be provided in order to find the actual equation.
Not a bad days work, eh?
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
I think that equation is a bit misleading. It seemed a good way to represent it as I wrote it, but now I see that the C(d) part is a bit confusing because the same function is used on the other side of that equation but it turns out that they are not really the same function.
What I should say is that the left hand side, C(d), is not actually a function call, but on the right hand side, C(1) or C( R(-d/c) ), it is a function call. That is because the right hand side is the implementation of the left hand side. Which means that they are not really the same function.
So let's clear that up.
Let:
R(t) be a function that must return the radius of a particle given a time differential, t, where t is in unit-time, for example, the number of seconds. When t=0, the current radius is returned. When t>0, a future radius is returned. When t<0, a past radius is returned.
C(r) be a function that returns the charge density at the boundary of a particle with radius r.
D(d) be a function that returns the charge density of a particle, measured at a distance, d, from its center.
c be the speed of light.
Therefore, the equation becomes:
D(d) = C( R( -d/c ) ) / d^3
I have also had some thoughts on the function C. If my memory serves me, then Miles has stated that the charge density of a body (he was talking about stars, planets and moons) is its mass times by its density. Quite literally a charge density or mass density. I am not so sure that I want the same equation because that assumes you want the total charge of the body. I don't really want that, although I could work with it.
You see, we are not only trying to find the charge density at a distance, we are also trying to find the charge density over a certain area which is defined by the receiver. So far, we have not taken the receiver into account at all but it is part of this interaction and so it must be represented.
To combat that, I thought the charge density function, C, could return the mass, of the emitter, divided by its surface area. This gives us a charge density per unit area. Now, this unit area is small on the emitter, but it could be extremely large at the receiver. How do we deal with that?
Well, we could not do what I have just mentioned (divide by the emitters surface area) and instead, we calculate the total charge output of the emitter, for a complete sphere, reduce it based on the distance to the receiver, and then divide it by the surface area of the sphere that is centered on the emitter, but with a radius equal to the distance of the measurement point (receiver). If the receiver is a volume, rather than a point, then we might multiply that result by the surface area of the receiver (or maybe half of it) to find the total charge density across the receiver.
I think this is very important stuff. I have not only found an equation that sits along side Einsteins' equations, which he had no way of knowing was needed, but I have also found a way to use Expansion Theory without actually expanding the radii of particles. In fact, I am really using it to contract the radii, but only when calculating a charge density, not during the normal run of the model.
If I can find a way to do the same thing with gravity, I will have the basis of an Expansion Model.
What I should say is that the left hand side, C(d), is not actually a function call, but on the right hand side, C(1) or C( R(-d/c) ), it is a function call. That is because the right hand side is the implementation of the left hand side. Which means that they are not really the same function.
So let's clear that up.
Let:
R(t) be a function that must return the radius of a particle given a time differential, t, where t is in unit-time, for example, the number of seconds. When t=0, the current radius is returned. When t>0, a future radius is returned. When t<0, a past radius is returned.
C(r) be a function that returns the charge density at the boundary of a particle with radius r.
D(d) be a function that returns the charge density of a particle, measured at a distance, d, from its center.
c be the speed of light.
Therefore, the equation becomes:
D(d) = C( R( -d/c ) ) / d^3
I have also had some thoughts on the function C. If my memory serves me, then Miles has stated that the charge density of a body (he was talking about stars, planets and moons) is its mass times by its density. Quite literally a charge density or mass density. I am not so sure that I want the same equation because that assumes you want the total charge of the body. I don't really want that, although I could work with it.
You see, we are not only trying to find the charge density at a distance, we are also trying to find the charge density over a certain area which is defined by the receiver. So far, we have not taken the receiver into account at all but it is part of this interaction and so it must be represented.
To combat that, I thought the charge density function, C, could return the mass, of the emitter, divided by its surface area. This gives us a charge density per unit area. Now, this unit area is small on the emitter, but it could be extremely large at the receiver. How do we deal with that?
Well, we could not do what I have just mentioned (divide by the emitters surface area) and instead, we calculate the total charge output of the emitter, for a complete sphere, reduce it based on the distance to the receiver, and then divide it by the surface area of the sphere that is centered on the emitter, but with a radius equal to the distance of the measurement point (receiver). If the receiver is a volume, rather than a point, then we might multiply that result by the surface area of the receiver (or maybe half of it) to find the total charge density across the receiver.
I think this is very important stuff. I have not only found an equation that sits along side Einsteins' equations, which he had no way of knowing was needed, but I have also found a way to use Expansion Theory without actually expanding the radii of particles. In fact, I am really using it to contract the radii, but only when calculating a charge density, not during the normal run of the model.
If I can find a way to do the same thing with gravity, I will have the basis of an Expansion Model.
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
I know I am getting pretty far off track, but this is so important that I just need to get it out. I need to run with it while it is fresh in my mind.
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
Note the differences between the quantum equation and the relativistic one.
1) D(d) = C(1)/d^3
2) D(d) = C( R( -d/c ) )/d^3
Equation 1 only has the value 1 inside of the C function call. This represents the current radius of the emitter.
Equation 2 has R( -d/c ) inside of the C call, which represents the radius of the emitter at some time in the past.
If we look at the definition of the R function, we find that when its argument is equal to 0, it will return the current radius.
When d is extremely small, the ratio of d to c approaches 0. It will never actually equal 0, but it will get so close as to be irrelevant.
Therefore, the relativistic equation reduces to the quantum equation at small distances.
1) D(d) = C(1)/d^3
2) D(d) = C( R( -d/c ) )/d^3
Equation 1 only has the value 1 inside of the C function call. This represents the current radius of the emitter.
Equation 2 has R( -d/c ) inside of the C call, which represents the radius of the emitter at some time in the past.
If we look at the definition of the R function, we find that when its argument is equal to 0, it will return the current radius.
When d is extremely small, the ratio of d to c approaches 0. It will never actually equal 0, but it will get so close as to be irrelevant.
Therefore, the relativistic equation reduces to the quantum equation at small distances.
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
.
You've definitely hit something, you've got to run with it. Including gravity would win you a seat beside Miles. The only thing I see missing is spin, then you can combine it with your angular motion and spin level velocity formulas.
Being critical, I might point out that emission fields aren’t spherical. The charged particle’s emission field is planar, like a disc, not a sphere. Actually, I would insist that a particle’s emission field may be better described as dual discs - due to the separate +/-30deg emissions. Or a neutron’s polar charge emissions have the least amount of energy since it receives no angular emission from the spinning particle, what’s the charge density range for polar emissions? My point is the particle’s emission field is more complicated than a spherical volume. I’ve insisted charge emission is a function of latitude. When we add the components necessary in order to arrive at a complete description of the particle’s emission field we may end up with a charge lookup table.
Good stuff Nevyn.
.
Ok, I'll try to read them. The charge density felt at distance d, depends on the emitter’s radius and the change in the emitter’s size in the time it took for light to reach the distance being measured, relativistic charge emission. -d/c approaches 0 for the quantum scale. Together, both equations combine the micro or macro scales based on an analysis of spherical volume. It reminds me of the fact that spherical surface area is used to describe the inverse relationship of gravity, how after doubling a radius, what was a unit area becomes an area four time as large. Not a bad days work at all. More like an epiphany, the particle scaling relationship you’ve been looking for.Quantum. D(d) = C(1)/d^3
Relativistic. D(d) = C( R( -d/c ) )/d^3
You've definitely hit something, you've got to run with it. Including gravity would win you a seat beside Miles. The only thing I see missing is spin, then you can combine it with your angular motion and spin level velocity formulas.
Being critical, I might point out that emission fields aren’t spherical. The charged particle’s emission field is planar, like a disc, not a sphere. Actually, I would insist that a particle’s emission field may be better described as dual discs - due to the separate +/-30deg emissions. Or a neutron’s polar charge emissions have the least amount of energy since it receives no angular emission from the spinning particle, what’s the charge density range for polar emissions? My point is the particle’s emission field is more complicated than a spherical volume. I’ve insisted charge emission is a function of latitude. When we add the components necessary in order to arrive at a complete description of the particle’s emission field we may end up with a charge lookup table.
Good stuff Nevyn.
.
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
LongtimeAirman wrote:
You've definitely hit something, you've got to run with it. Including gravity would win you a seat beside Miles.
I think including gravity will earn me a seat next to Einstein. Maybe even above Einstein! I'm not trying to make myself sound great or anything, there's still so much I don't know, but if I do that, then I have actually done what Einstein said that he did, but didn't quite get it correct, or at least complete.
But I'm still doubting myself at this point. I keep re-reading it to make sure I haven't missed anything or buggered something up. I don't care about being compared to Einstein, just that we figure out Physics before it's too late. I am standing on the shoulders of both Miles and Einstein here, and give that credit where it is due. There is absolutely no way that I would have reached this position without Miles work behind me. None at all.
LongtimeAirman wrote:
The only thing I see missing is spin, then you can combine it with your angular motion and spin level velocity formulas.
Ah, but as we have already implemented in this app, spin comes from measuring the charge interactions from multiple places on the receiver and applying them in the correct fashion. We've already completed that step!
LongtimeAirman wrote:
Being critical, I might point out that emission fields aren’t spherical. The charged particle’s emission field is planar, like a disc, not a sphere. Actually, I would insist that a particle’s emission field may be better described as dual discs - due to the separate +/-30deg emissions. Or a neutron’s polar charge emissions have the least amount of energy since it receives no angular emission from the spinning particle, what’s the charge density range for polar emissions? My point is the particle’s emission field is more complicated than a spherical volume. I’ve insisted charge emission is a function of latitude. When we add the components necessary in order to arrive at a complete description of the particle’s emission field we may end up with a charge lookup table.
Totally true and well done for seeing it so quickly. However, we have already fixed that problem in this app too! My charge density algorithm, already in use, takes care of the latitude differences. That algorithm would be inside of the C function used in those equations. It does need more work, though, especially around the polar regions. It would also be nice if I could reduce it to an equation rather than an algorithm. I'm not sure that is possible.
My main concern at this point is the R function. I'm just not sure how to go about implementing that. While I have some idea of what the C function looks like, figuring out the radius changes is a bit more difficult. I am hoping that I find that gravity is not really a 1/r^2 relationship. I am hoping that I find the same thing I did here, that one of those distances is actually a time separation and will not be required in the math, in that way. Miles has already said as much, but I don't think he has taken that concept down to the equations like I am trying to here.
To bring this back down to Earth, and demonstrate that I don't have an expanding ego, all I am doing here is analyzing geometry. I decided to go back to basics to determine how charge diminishes so that I could find the spot that I needed to change it, and have found a few things in the process. I am not doing anything that would be considered great, or of high intelligence. How many times has Miles said that science has gotten so far ahead of itself and just needs to get back to basics? And again we find it here. Physics doesn't need intelligence, it only needs mechanics. When you have the mechanics, the math just falls out of it. The mechanics controls the math. It provides the boundaries that the math must follow. It gives you the concepts that the math must implement.
So the next time you hear a Physicist say that the 'math is everything', you know they are lying. If the mechanics control the math, then the mechanics is more important than the math. That is because the mechanics represents reality and if your math is not tied to reality, then it is not Physics.
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
Something else I would like to point out is that it is Expansion Theory that has allowed me to find this stuff. By reducing gravity to a changing radius, a real motion of real entities, Miles has provided the basis for the mechanics that I needed. All I did was notice that I needed a smaller radius to represent the past (again provided by Miles), and that I had a radius in such a position. So I ran with it and am pretty happy with where I have ended up.
There is still a lot of work required, but what I have found, in only a few hours, is a great start. I not only have the general structure of the equation, I also have the placeholders for future work. And they are not just undefined placeholders either, they are clearly defined. While I don't know their exact implementations right now, I do know what they need to do.
When was the last time you saw that in mainstream Physics?
Aaaaaand, my ego is expanding again. Does anyone have a pin?
There is still a lot of work required, but what I have found, in only a few hours, is a great start. I not only have the general structure of the equation, I also have the placeholders for future work. And they are not just undefined placeholders either, they are clearly defined. While I don't know their exact implementations right now, I do know what they need to do.
When was the last time you saw that in mainstream Physics?
Aaaaaand, my ego is expanding again. Does anyone have a pin?
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
Jesus, Nevyn.
I'll be that pin, but only because you've been my pin in the past. Consider it returning the favor!
But this is some good shit right here. I'm not at all familiar with the ins and outs of the app or the script you're using, but ALL of the expansion equations here and your explanation makes sense to me. You're attacking it in a way that would have never occurred to me. It's definitely what you think, an extension of Miles and Einstein and all the other works but in a revolutionary way here. I think you need to keep going, and only wish I had the capacity to help aside from cheerleading. But it's something I might be able to plop into Maya as well, since it's so straightforward! Perhaps all of this scripting can be fairly easily converted to Python or Pymel, and save me all the headaches I've had with the Ndynamics "Nucleus" solver (ironic since it can't handle an actual nucleus!).
Allow yourself some patience though too! But as is your wont, run with it as far and fast as you can. You can always refine it later.
I'll be that pin, but only because you've been my pin in the past. Consider it returning the favor!
But this is some good shit right here. I'm not at all familiar with the ins and outs of the app or the script you're using, but ALL of the expansion equations here and your explanation makes sense to me. You're attacking it in a way that would have never occurred to me. It's definitely what you think, an extension of Miles and Einstein and all the other works but in a revolutionary way here. I think you need to keep going, and only wish I had the capacity to help aside from cheerleading. But it's something I might be able to plop into Maya as well, since it's so straightforward! Perhaps all of this scripting can be fairly easily converted to Python or Pymel, and save me all the headaches I've had with the Ndynamics "Nucleus" solver (ironic since it can't handle an actual nucleus!).
Allow yourself some patience though too! But as is your wont, run with it as far and fast as you can. You can always refine it later.
Jared Magneson- Posts : 525
Join date : 2016-10-11
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
.
Jared, I don't know about you, but I'm not script smart. I'd be more than happy to work with you to learn this app to the extent that you might need it. Helping you would help me learn it. I can't say I can teach it since there's a great deal about it I haven't begun to figure out and it's not finished yet. As Nevyn says, programming is a tool. It's more important to understand how to work with it.
I’ve got a tack for you Nevyn, but fair’s fair, you deserve credit. By expansion theory, we know charge particles are expanding. We also know, given an interval of time, a charged particles’ emissions will expand outward from the particle, as on an expanding spherical layer. Have you told us something we don’t know? I don’t think so. On the other hand, I believe this development of yours improves our understanding of relativity. Now we can say – of course! We can clearly see the both the expanding charge particle and its expanding emission field, easily adjusting for micro or macro.
I'm surprised you feel implementing the R function is a problem. I believe we already know the radius function R. All objects in the universe are expanding – accelerating - at the same rate. For Earth, the radius doubles every 19 minutes or so. Why there’s a post or two on the subject here at this site. As requested, just poking.
All radii and distances are time dependent variables – the relativistic perspective. We know that the particle radius should be time dependent, equal to a distance, r0 at some position p0 at time t0, r(t)= p(0) + r(0)*expansion(t). Normally one can overlook such details, but if you’re trying to model the universe, relativity must be included. Previously I could always claim I didn't understand relativity, but that excuse is worn pretty thin now, although you or Miles have always surprised me with things I hadn’t considered.
So the CPIM app already includes spin and a latitude function – great, it may go all the way. With all due respect, when I said you should use spin to tie all your formulas together, app aside, the physics comes first. If you’ve already built CPIM with these ideas in mind, not just a charge field but a relativistic charge field I’d say you’re doing a fine job.
Otherwise, as we're all aware, it's not quite done. It needs gravity - or this great new expansion alternative you're putting together.
.
Jared, I don't know about you, but I'm not script smart. I'd be more than happy to work with you to learn this app to the extent that you might need it. Helping you would help me learn it. I can't say I can teach it since there's a great deal about it I haven't begun to figure out and it's not finished yet. As Nevyn says, programming is a tool. It's more important to understand how to work with it.
I’ve got a tack for you Nevyn, but fair’s fair, you deserve credit. By expansion theory, we know charge particles are expanding. We also know, given an interval of time, a charged particles’ emissions will expand outward from the particle, as on an expanding spherical layer. Have you told us something we don’t know? I don’t think so. On the other hand, I believe this development of yours improves our understanding of relativity. Now we can say – of course! We can clearly see the both the expanding charge particle and its expanding emission field, easily adjusting for micro or macro.
I'm surprised you feel implementing the R function is a problem. I believe we already know the radius function R. All objects in the universe are expanding – accelerating - at the same rate. For Earth, the radius doubles every 19 minutes or so. Why there’s a post or two on the subject here at this site. As requested, just poking.
All radii and distances are time dependent variables – the relativistic perspective. We know that the particle radius should be time dependent, equal to a distance, r0 at some position p0 at time t0, r(t)= p(0) + r(0)*expansion(t). Normally one can overlook such details, but if you’re trying to model the universe, relativity must be included. Previously I could always claim I didn't understand relativity, but that excuse is worn pretty thin now, although you or Miles have always surprised me with things I hadn’t considered.
So the CPIM app already includes spin and a latitude function – great, it may go all the way. With all due respect, when I said you should use spin to tie all your formulas together, app aside, the physics comes first. If you’ve already built CPIM with these ideas in mind, not just a charge field but a relativistic charge field I’d say you’re doing a fine job.
Otherwise, as we're all aware, it's not quite done. It needs gravity - or this great new expansion alternative you're putting together.
.
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
No, I haven't shown anything we didn't already know, but I have used it in a more logical, consistent, and precise manner.
I don't know where that doubling every 19 minutes comes from, so I don't know if I can trust it. Doubling is also a relative term, so it doesn't really tell us anything about the actual radius. You also have to know what that 19 minutes applies to. You see, from a non-expanding perspective, both distance and time expand, since time is based on distance. If the meter expands, then so does the second. This keeps the ratio the same in spite of the expansion, from an expanding perspective. I am trying to find math that fills the gap between what we see from an expanding perspective and what really happens from a non-expanding perspective. I am not exactly in either camp, but somewhere between them. I need to step through it with great care to keep everything in its proper place.
Finding this change in radius will actually allow me to implement gravity at the same time. Since that change in radius is gravity. I just need to account for time discrepancies. I'm looking over Miles Third Wave papers for equations I can use and have found a few, but I'm still trying to figure out exactly how he calculated an initial radius for the proton. Miles states that you can't just use the equations of motions to find an older radius, or you can but you can only use it as a proportionality. I found another equation this morning, but haven't had any time to play with it.
I don't know where that doubling every 19 minutes comes from, so I don't know if I can trust it. Doubling is also a relative term, so it doesn't really tell us anything about the actual radius. You also have to know what that 19 minutes applies to. You see, from a non-expanding perspective, both distance and time expand, since time is based on distance. If the meter expands, then so does the second. This keeps the ratio the same in spite of the expansion, from an expanding perspective. I am trying to find math that fills the gap between what we see from an expanding perspective and what really happens from a non-expanding perspective. I am not exactly in either camp, but somewhere between them. I need to step through it with great care to keep everything in its proper place.
Finding this change in radius will actually allow me to implement gravity at the same time. Since that change in radius is gravity. I just need to account for time discrepancies. I'm looking over Miles Third Wave papers for equations I can use and have found a few, but I'm still trying to figure out exactly how he calculated an initial radius for the proton. Miles states that you can't just use the equations of motions to find an older radius, or you can but you can only use it as a proportionality. I found another equation this morning, but haven't had any time to play with it.
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
I found the pin!
While the above analysis is still applicable, I have started from the wrong position. It is not volume that I should be analyzing, but surface area. My method is still the same, but we start from SA = 4Pi * r^2.
Which gives us a 1/r^2 relationship.
Therefore, to find the charge at a given distance, we use: D(d) = C(1)/d^2
The relativistic version is: D(d) = C( R( -d/c ) )/d^2
Miles then went on to include gravity, which he said brings in another 1/r^2 relationship, so we end up with 1/r^4. However, I stand by my analysis and in the case of charge density, gravity must be included in the initial determination of charge density at the boundary of the emitter.
While the above analysis is still applicable, I have started from the wrong position. It is not volume that I should be analyzing, but surface area. My method is still the same, but we start from SA = 4Pi * r^2.
| Radius | Area | A(r) / A(1) | A(1) / A(r) |
| 1 | 12.5663706144 | 1 | 1 |
| 2 | 50.2654824574 | 4 | 0.25 |
| 3 | 113.0973355292 | 9 | 0.11111111 |
| 4 | 201.0619298297 | 16 | 0.0625 |
| 5 | 314.159265359 | 25 | 0.04 |
| 6 | 452.3893421169 | 36 | 0.0277777778 |
| 7 | 615.7521601036 | 49 | 0.0204081633 |
| 8 | 804.247719319 | 64 | 0.015625 |
| 9 | 1017.8760197631 | 81 | 0.012345679 |
| 10 | 1256.6370614359 | 100 | 0.01 |
Which gives us a 1/r^2 relationship.
Therefore, to find the charge at a given distance, we use: D(d) = C(1)/d^2
The relativistic version is: D(d) = C( R( -d/c ) )/d^2
Miles then went on to include gravity, which he said brings in another 1/r^2 relationship, so we end up with 1/r^4. However, I stand by my analysis and in the case of charge density, gravity must be included in the initial determination of charge density at the boundary of the emitter.
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
To be clear, charge density is a function of the volume of the emitter at the time of emission. It is the emission of a volume, over a surface. However, the drop-off of that emission is only dependent on surface area. We are taking the emission of 1 dt, and watching it as it moves out into space. We don't care about the space between that emission and its source, which using volume would include, so we use the surface area equation.
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
That makes perfect sense to me, Nevyn. The math even makes sense, which is a good thing since I'm not great with these kinds of maths and would have never seen these relationships the way you do.
I apologize to just be a sort of cheerleader here, but it's still interesting and I'm trying to follow along as best I can. Wish I could actually help on this one though.
I apologize to just be a sort of cheerleader here, but it's still interesting and I'm trying to follow along as best I can. Wish I could actually help on this one though.
Last edited by Jared Magneson on Mon Aug 13, 2018 9:59 pm; edited 1 time in total
Jared Magneson- Posts : 525
Join date : 2016-10-11
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
.
That makes sense to me. You may have noticed I've been thinking of your finding strictly in terms of surface area. In my last post I interpreted your 'emission volume' as an expanding dt surface - "We also know, given an interval of time, a charged particles’ emissions will expand outward from the particle, as on an expanding spherical layer". The entire emission volume would involve all subsequent time differentials which we don't need.
.
That makes sense to me. You may have noticed I've been thinking of your finding strictly in terms of surface area. In my last post I interpreted your 'emission volume' as an expanding dt surface - "We also know, given an interval of time, a charged particles’ emissions will expand outward from the particle, as on an expanding spherical layer". The entire emission volume would involve all subsequent time differentials which we don't need.
.
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
Yeah, I was thinking the same way, only really seeing it as the top layer of the volume, but still didn't put it together that I should be using the surface area instead. Miles had to remind me as I looked over one of his papers. But my method is sound and it was only the initial equation that needed to be fixed, so the general outcome is the same.
It is good to know that you can understand what I have written. That I am making sense. So you are doing a bit more than just cheer-leading. I want to show how I find these things, and why the math is the way it is, so others can see what being mechanical means. So they can run with it themselves and maybe find things that everyone else has missed.
It is good to know that you can understand what I have written. That I am making sense. So you are doing a bit more than just cheer-leading. I want to show how I find these things, and why the math is the way it is, so others can see what being mechanical means. So they can run with it themselves and maybe find things that everyone else has missed.
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
Let's have a look at the Radius function.
The radius function, R, must return the radius of a particle given a time differential, t, where t is in unit-time, for example, the number of seconds. When t=0, the current radius is returned. When t>0, a future radius is returned. When t<0, a past radius is returned.
We use the equation of motion s = (at^2)/2 to find the displacement of the radius given the time it occurs over, and the acceleration of the radius. We already know the time, d/c, but we need to know the value of gravity. I have found differing values for the gravity of the proton and need to decipher which one is applicable and why. For now, we will let it stand as the variable a.
Let:
r = current radius of emitter
a = gravity of emitter
t = amount of time the motion occurs over
Then:
If t < 0
R(t) = r - at^2 / 2
Else
R(t) = r + at^2 / 2
Unfortunately, passing in a negative time does not work as well in the math as I wanted it to. The time is squared which means the negative sign is lost so it needs to be extracted from the time or used in a different way to avoid this. I am going to redefine the R function so that it doesn't need to handle that part.
Let R be a function that returns the change in radius given an amount of time, t, where t>=0.
That leaves the subtraction from the current radius out of the R function and we can deal with the minus sign because we know that we are moving backwards in time in this equation.
So R becomes:
R(t) = (at^2)/2
Putting that into D gives us:
D(d) = C( r - R( d/c ) )/d^2
= C( r - (a/2)(d/c)^2 )/d^2
Now we can see a bit more clearly why the relativistic equation reduces to the quantum version. I said earlier that as d becomes very small, the ratio of d:c approaches 0. In the above equation, that causes the change in radius to be so small that it can be thought of as just being the radius. i.e. r - (a/2)0^2 = r.
The values for r and a are treated as constants here, but they really represent the emitter. It might be a proton or it might be a star. For a given problem they may be constants but in others they will need to be specified. So I would rewrite the equation like this:
D( r, a, d ) = C( r - (a/2)(d/c)^2 )/d^2
to reflect that r, a, and d are all parameters. I'm not sure if that is how mathematicians specify such things but I know programmers will understand.
The radius function, R, must return the radius of a particle given a time differential, t, where t is in unit-time, for example, the number of seconds. When t=0, the current radius is returned. When t>0, a future radius is returned. When t<0, a past radius is returned.
We use the equation of motion s = (at^2)/2 to find the displacement of the radius given the time it occurs over, and the acceleration of the radius. We already know the time, d/c, but we need to know the value of gravity. I have found differing values for the gravity of the proton and need to decipher which one is applicable and why. For now, we will let it stand as the variable a.
Let:
r = current radius of emitter
a = gravity of emitter
t = amount of time the motion occurs over
Then:
If t < 0
R(t) = r - at^2 / 2
Else
R(t) = r + at^2 / 2
Unfortunately, passing in a negative time does not work as well in the math as I wanted it to. The time is squared which means the negative sign is lost so it needs to be extracted from the time or used in a different way to avoid this. I am going to redefine the R function so that it doesn't need to handle that part.
Let R be a function that returns the change in radius given an amount of time, t, where t>=0.
That leaves the subtraction from the current radius out of the R function and we can deal with the minus sign because we know that we are moving backwards in time in this equation.
So R becomes:
R(t) = (at^2)/2
Putting that into D gives us:
D(d) = C( r - R( d/c ) )/d^2
= C( r - (a/2)(d/c)^2 )/d^2
Now we can see a bit more clearly why the relativistic equation reduces to the quantum version. I said earlier that as d becomes very small, the ratio of d:c approaches 0. In the above equation, that causes the change in radius to be so small that it can be thought of as just being the radius. i.e. r - (a/2)0^2 = r.
The values for r and a are treated as constants here, but they really represent the emitter. It might be a proton or it might be a star. For a given problem they may be constants but in others they will need to be specified. So I would rewrite the equation like this:
D( r, a, d ) = C( r - (a/2)(d/c)^2 )/d^2
to reflect that r, a, and d are all parameters. I'm not sure if that is how mathematicians specify such things but I know programmers will understand.
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
.
After rereading a couple of Miles’ third wave and part of his long Mercury precession papers earlier today, I’d say you’re using the motion equation s = (at^2)/2, to find the displacement of the radius exactly as Miles has done.
Critically speaking, that’s all I’ve got.
You’re making charge field history. What next?
.
I’m sure mathematicians and programmers would agree, D( r, a, d ) appears radical. The charge density received from a charged particle depends on the particle’s radius, gravity and distance. Standard math doesn’t list all the parameters used on the right side of an identity equation as an index, or whatever that is, on the left. I would say a - the gravity of the emitter - is the only emitter “constant”. It’s difficult to tell the difference between distances and an acceleration without accompanying units - meters, seconds or sec^2.So I would rewrite the equation like this:
D( r, a, d ) = C( r - (a/2)(d/c)^2 )/d^2
to reflect that r, a, and d are all parameters. I'm not sure if that is how mathematicians specify such things but I know programmers will understand.
After rereading a couple of Miles’ third wave and part of his long Mercury precession papers earlier today, I’d say you’re using the motion equation s = (at^2)/2, to find the displacement of the radius exactly as Miles has done.
Critically speaking, that’s all I’ve got.
You’re making charge field history. What next?
.
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
Yeah, I thought it would be non-conformant, but I wanted to express that they may be variables in some circumstances while they may be constants in others. This is especially true when dealing with stars, planets and moons. Every entity will have its own radius and gravity value, where-as if we are looking at protons, then they all share the same values for those. But electrons and neutrons will be different, so it isn't just a micro vs macro type of thing. Even for our purposes in this app, we will need to handle different values once we bring electrons into the mix. We could probably use the same values for protons and neutrons though.
What's next?
Seriously though, I am working on the Charge Density function, C, to figure out if charge density can be calculated in the way that I want it to be. I want an expression that gives us the charge density, but only for a unit-area of the emitter, that can then be expressed on the receiver.
Question: What do you get if you take the volume of a sphere and divide it by the surface area of that sphere?
Conceptually, you should get the volume per unit-area.
A Dimensional Analysis tells you that the value is a meter (assuming you are using meters as your length units). It is 1 dimensional, not 3, so how does it represent a volume? Because it is a radius!
If you take the equation for the volume of a sphere (4/3 * PI * r^3) and divide it by the equation for the surface area of a sphere (4 * PI * r^2), you get r/3. Therefore, if my interpretation is correct, the volume per unit-area is equal to the volume of a sphere with a radius that is 1/3 of the original sphere's radius.
Does that sound reasonable?
Also, gravity. With the equation s = at^2/2, we can find the change in radius given an amount of time (which will be the time between frames but also include any time discrepancy as a result of distance separation) to find the amount of space that the other particles have taken up as a result of their expansion. We convert that into a vector that pulls our particle in that direction, by that amount. We do that for every other particle and sum them all together to get a resultant gravity vector. I'm not sure this is correct, since the other particles will expand regardless of what our current particle is doing. But in this math, 2 particles on either side of our particle will result in no motion. It doesn't feel quite right, but I can't see another way to do it, yet.
What's next?
Brain, in every episode of Pinkie and the Brain, wrote:The same thing we do every night, Pinkie, plan to take over the world!
Seriously though, I am working on the Charge Density function, C, to figure out if charge density can be calculated in the way that I want it to be. I want an expression that gives us the charge density, but only for a unit-area of the emitter, that can then be expressed on the receiver.
Question: What do you get if you take the volume of a sphere and divide it by the surface area of that sphere?
Conceptually, you should get the volume per unit-area.
A Dimensional Analysis tells you that the value is a meter (assuming you are using meters as your length units). It is 1 dimensional, not 3, so how does it represent a volume? Because it is a radius!
If you take the equation for the volume of a sphere (4/3 * PI * r^3) and divide it by the equation for the surface area of a sphere (4 * PI * r^2), you get r/3. Therefore, if my interpretation is correct, the volume per unit-area is equal to the volume of a sphere with a radius that is 1/3 of the original sphere's radius.
Does that sound reasonable?
Also, gravity. With the equation s = at^2/2, we can find the change in radius given an amount of time (which will be the time between frames but also include any time discrepancy as a result of distance separation) to find the amount of space that the other particles have taken up as a result of their expansion. We convert that into a vector that pulls our particle in that direction, by that amount. We do that for every other particle and sum them all together to get a resultant gravity vector. I'm not sure this is correct, since the other particles will expand regardless of what our current particle is doing. But in this math, 2 particles on either side of our particle will result in no motion. It doesn't feel quite right, but I can't see another way to do it, yet.
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
Brain, in every episode of Pinkie and the Brain, wrote:
The same thing we do every night, Pinkie, plan to take over the world!
Lol!!!
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
.
Pinky and the Brain are about to implement gravity.

Curious about the outcome? See: animaniacs pinky and the brain
https://gifer.com/en/oaf
////\\\\////\\\\////\\\\////\\\\////
I thought we were going to implement gravity by redrawing expanding particles. The screen dimensions would need to be recalculated along with the acceleration of the expanding particles.
.
Pinky and the Brain are about to implement gravity.

Curious about the outcome? See: animaniacs pinky and the brain
https://gifer.com/en/oaf
////\\\\////\\\\////\\\\////\\\\////
I thought we were going to implement gravity by redrawing expanding particles. The screen dimensions would need to be recalculated along with the acceleration of the expanding particles.
.
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
.
Sorry Nevyn, I don't understand your resultant gravity vector idea. If particles are outside each other's charge range will gravity still be calculated? Real expanding particles seems easier.
Concerning the reasonableness of the notion of a volume of a sphere divided by the sphere’s surface area. You’ve shown how they – the surface area and volume - are related. A “volume of particle emission” becomes an expanding spherical layer, a surface area with a differential time thickness dt. The further an object is, the smaller the amount of the expanding surface area the receiver will intercept. Sounds perfectly reasonable to me.
.
Sorry Nevyn, I don't understand your resultant gravity vector idea. If particles are outside each other's charge range will gravity still be calculated? Real expanding particles seems easier.
Concerning the reasonableness of the notion of a volume of a sphere divided by the sphere’s surface area. You’ve shown how they – the surface area and volume - are related. A “volume of particle emission” becomes an expanding spherical layer, a surface area with a differential time thickness dt. The further an object is, the smaller the amount of the expanding surface area the receiver will intercept. Sounds perfectly reasonable to me.
.
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
.
Area and Volume of a Circle and Sphere Using Simple Geometry
http://physicsinsights.org/sphere-volume-1.html
I don't see a problem. Check your thinking against this site.Therefore, if my interpretation is correct, the volume per unit-area is equal to the volume of a sphere with a radius that is 1/3 of the original sphere's radius.
Area and Volume of a Circle and Sphere Using Simple Geometry
http://physicsinsights.org/sphere-volume-1.html
.(14) Volume(sphere) = (1/3)*r*A
where A now represents the surface area of the sphere. ...
(15)The Surface(sphere) = 4Pi*r^2
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
LongtimeAirman wrote:
I thought we were going to implement gravity by redrawing expanding particles. The screen dimensions would need to be recalculated along with the acceleration of the expanding particles.
No, we can't do that for at least 2 reasons. The first one mathematical and the second physical.
1) The numbers explode!
We are working within a certain precision which is set by the computer that the application is running on and the language used to implement it. In our case, we have 64bit floating point numbers in Javascript, but on a GPU, such as in a shader, we may only have 32bit floating point values. On a phone, we might only have 16bit numbers. No matter how large that is, it is still finite. We could be working with 1024bit numbers and it still would not be enough. If you just keep increasing the radii, then you will eventually, actually rather quickly, reach the upper limit of what your numbers can store.
There are ways around this limit. You can work with arbitrarily sized numbers that do not have an upper limit, except for the amount of memory in your system. However, they introduce a speed limit. The larger your numbers are, the slower they are to use in any calculation. Eventually, again rather quickly, the app grinds to a halt just trying to add 2 numbers together.
2) It doesn't represent the actual physics.
A 3D system is a Newtonian system, rather than a Relativistic one. The 3D engine will render all geometry as it is now, no matter how far it is from the camera. It does take distance into account to make things smaller the further they are from the camera, but it does not take the time discrepancy that that distance represents into account. We can make it do that, but only with considerable effort, and it is not as easy as it first looks.
You see, it isn't just the size that we see in the past, it is also the position (and velocity, spin, etc). When we look at the Sun from the Earth, we are seeing it at a size that it was 8 minutes ago, but we are also seeing it in the position that it was in 8 minutes ago. This is also a problem for charge calculations. My equation above takes care of the time discrepancy by using a smaller radius to calculate the initial emission, but it does not take the position difference into account. In its current state, it can't do that. In fact, it might not be feasible to do that because while that charge was travelling from the source to the receiver, the emitter could have had a collision and changed trajectory. We have no way of knowing that.
So we are left to find another way. It isn't going to be perfect, but we may be able to get pretty close and hopefully minimize the differences.
My idea is to treat everything as if it is always at the same size, but use adjusted values from all other particles that the current particle is interacting with. You always need a reference point, which is the current particle for us, so that you can determine how things look from that point. They may look completely different from a different point, but that is irrelevant to our current particle, for it is not over there, it is here.
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
LongtimeAirman wrote:Sorry Nevyn, I don't understand your resultant gravity vector idea. If particles are outside each other's charge range will gravity still be calculated? Real expanding particles seems easier.
I'm not sure about that. There is some distance where the change becomes so small as to be irrelevant. We can choose to find that distance and ignore everything outside of it just like we are with charge. Or we might just add it in anyway. It will probably be just as much computational effort to determine if it is too far away as it is to just calculate and add it in, which is not the case with charge as that is expensive to calculate.
LongtimeAirman wrote:Concerning the reasonableness of the notion of a volume of a sphere divided by the sphere’s surface area. You’ve shown how they – the surface area and volume - are related. A “volume of particle emission” becomes an expanding spherical layer, a surface area with a differential time thickness dt. The further an object is, the smaller the amount of the expanding surface area the receiver will intercept. Sounds perfectly reasonable to me.
Not quite correct. Or it is in some ways, but maybe a bit misleading. The further an emitter is from the receiver, the larger the surface area is at the location of the receiver. That is, if we calculate a unit-area on the emitter at the time of emission, then that unit-area expands as that emission travels away from the emitter. That is what the outer 1/d^2 is doing in my equation. It is finding the amount of emission over the same unit-area on the receiver and the d^2 reduces the charge density to reflect the same unit-area at the receiver. The unit-area stays the same and we let the charge density change but we could just as easily find the new area that the emission covers at the receiver.
In fact, I think we should do that. We should let the emission travel out uninhibited until it reaches the receiver. We then calculate the size of the original unit-area at that distance. Then we divide that, let's call it the received-area, by the area that it interacts with on the receiver. This creates an equation that calculates the interaction of one area, on the emitter, and another area, on the receiver. Therefore, it can handle the difference in area that the receiver has with respect to the emitter. I might investigate that at some point. It may just lead to the same 1/d^2 relationship, but it is worth finding out.
LongtimeAirman wrote:I don't see a problem. Check your thinking against this site.
Area and Volume of a Circle and Sphere Using Simple Geometry
http://physicsinsights.org/sphere-volume-1.html
I knew the math was correct, not because I searched for it, but because I plugged some values into it and saw the relationship directly. What I am unsure of is my interpretation of it being the radius of a sphere to represent a volume. That site does not explicitly state it, but I was using the same concepts as they are (as in a pyramid-like shape from the surface to the center).
What I am trying to get at with that analysis, is that it is the whole volume that is emitting, not just the surface, even though it only emits at the surface. How can that be? Easy, because not all of that emission was created (for want of a better term) at the same time, but it is all emitted from the surface at the same time.
This is easier to see with stars and planets, than protons or small particles. I am actually wondering if there is a different equation for particles as compared to composite entities like stars. Anyway, with a star or planet, we have a body made up of smaller particles and it is each of those particles that is actually emitting. The sum of that emission becomes the emission of the body. However, the emission that came from the very center of that body is older than the emission that came from the surface particles. But age doesn't really matter. It is the sum of emission at the surface that we care about because that is the amount of emission that will travel away from the emitter and eventually collide with a receiver.
That gets us the total charge emission from the volume (with an assumption that the whole sphere is emitting, which we know is incorrect) at the surface. I then divided that by the surface area to get to a unit-volume or the amount of volume that is behind a unit-area. That should represent the amount of emission that is moving towards the receiver, with some margin of error. What we really should do, is determine the surface area of reception, translate that into an area of emission and use that to calculate the amount of emission. I may investigate that as well.
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
I had an idea a few months ago that might be able to help us here. In my posts above, I mentioned that there is a problem with reaching back into the past because you can only use the current data to do so. This ignores any interactions between the time of emission and reception that might have occurred to the emitter because there is no way to determine that. The best we could do is assume a reversal of the current velocity, spin, etc, which is not really good enough. It might work okay with stars and planets, but not at all with particles. Although, particles have an advantage in that they are so close to each other that we aren't looking very far into the past, but they also collide a lot more often and the results of those collisions are more drastic if compared to a planet.
The idea I had was to look at everything as an event. Each event has a time that it occurred, the position and orientation it was in, the resultant velocity and spin, etc. Essentially, it is the state of the entity at that event, or just after that event really. From there, we can determine its current position and orientation by using the time since that event and apply it to the velocity and spin. So we never change the position of an entity, for example, we just calculate its current one. Only a collision, which is the event, can cause those values to change.
Now, we can extend that a bit to keep a certain amount of history. We store the last 10 events, for example, so we can actually determine the complete story of that entity at least that far back into the past. We have a path, not just a line. Jared will be familiar with this because it is the basis of keyframes that he works with. However, he is using it to drive the complete animation, where-as I just want a window of it to represent the past.
The idea I had was to look at everything as an event. Each event has a time that it occurred, the position and orientation it was in, the resultant velocity and spin, etc. Essentially, it is the state of the entity at that event, or just after that event really. From there, we can determine its current position and orientation by using the time since that event and apply it to the velocity and spin. So we never change the position of an entity, for example, we just calculate its current one. Only a collision, which is the event, can cause those values to change.
Now, we can extend that a bit to keep a certain amount of history. We store the last 10 events, for example, so we can actually determine the complete story of that entity at least that far back into the past. We have a path, not just a line. Jared will be familiar with this because it is the basis of keyframes that he works with. However, he is using it to drive the complete animation, where-as I just want a window of it to represent the past.
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
.
You're covering new ground, I may not be the only one with a confusion or two. Must have pictures. Feel free to mark or make corrections or suggestions.

The emitter is on the left, and the receiver is on the right. You’ve recently developed a relativistic charge field, based on expansion theory, where charge emitted - C(), the particle radius - R() and the amount of charge received - D() allow us to model charged particles of almost any size, quantum or stellar.
Currently, the charge density received calculation is done at the receiver’s N/S,E/W,F/B points. I believe that this method doesn’t seem capable of differentiating between a relativistic case or not, so you are coming up with a better method.
I'm not sure I understand your r/3 spherical volume. I would say that the volume of the sphere that is the source for all emission felt by the receiver is the small conic section of the emitter, the base of the conic section is pointed toward the receiver. We can see the expansion of the surface area intercepted by the receiver.
.
You're covering new ground, I may not be the only one with a confusion or two. Must have pictures. Feel free to mark or make corrections or suggestions.

The emitter is on the left, and the receiver is on the right. You’ve recently developed a relativistic charge field, based on expansion theory, where charge emitted - C(), the particle radius - R() and the amount of charge received - D() allow us to model charged particles of almost any size, quantum or stellar.
Currently, the charge density received calculation is done at the receiver’s N/S,E/W,F/B points. I believe that this method doesn’t seem capable of differentiating between a relativistic case or not, so you are coming up with a better method.
I'm not sure I understand your r/3 spherical volume. I would say that the volume of the sphere that is the source for all emission felt by the receiver is the small conic section of the emitter, the base of the conic section is pointed toward the receiver. We can see the expansion of the surface area intercepted by the receiver.
.
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
Nevyn wrote:Jared will be familiar with this because it is the basis of keyframes that he works with. However, he is using it to drive the complete animation, where-as I just want a window of it to represent the past.
Indeed, and ideally my simulations would (and will) borrow as much from yours as possible. I just don't know how to get it into Maya yet really! Obviously keyframes and editing are useful for a video-style presentation, but the simulation itself needs to be on or approach this level for me at some point. I'm following along pretty well, though you still work some serious magic to me. And really appreciate what you guys are doing here.
Jared Magneson- Posts : 525
Join date : 2016-10-11
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
Sorry for the confusion, I'm just playing with ideas. Seeing what's possible. Some of those ideas are not for this app, but are in the same area. There isn't one magic equation for everything. There are little subtleties that can change the equations you want to use in a given problem or you might want a different kind of information so you go about it in a different way. I am not being clear about that at all. I'm just dumping my thoughts at this stage and seeing if they can stand up by themselves. Not very fair to anyone trying to understand me!
The use of charge points (N,S,E,W,F,B, for example) is still viable and the way I want to go. I'm quite proud of that little algorithm! It has no relation to being relativistic because the charge points are about applying the charge to the receiver, where-as being relativistic is about supplying charge by the emitter. It is the emission that happened in the past maybe because it is a long way away. The reception of that charge is a local event. It happens now, so no need for Relativity on that side of the interaction. If you want to know if something is, or needs to be, relativistic, just look for time discrepancies. They can be masked as distances.
Yes, it is the conic section that I was trying to get at. We want to know how much volume is in that section as that is the amount of charge that the receiver has to deal with. If we imagine that where that conic section touches the surface is a unit-area, then that whole conic section is a unit-volume. If my interpretation is correct, then that section has a volume that is equal to the volume of a sphere with 1/3rd of the radius of this sphere. So imagine that we take the sphere, create another sphere that has 1/3rd the radius, and then squash that smaller sphere into the shape of the conic section. It should match. That's all I'm trying to say about that. It seems logical to me, but am open to criticism as well.
The use of charge points (N,S,E,W,F,B, for example) is still viable and the way I want to go. I'm quite proud of that little algorithm! It has no relation to being relativistic because the charge points are about applying the charge to the receiver, where-as being relativistic is about supplying charge by the emitter. It is the emission that happened in the past maybe because it is a long way away. The reception of that charge is a local event. It happens now, so no need for Relativity on that side of the interaction. If you want to know if something is, or needs to be, relativistic, just look for time discrepancies. They can be masked as distances.
Yes, it is the conic section that I was trying to get at. We want to know how much volume is in that section as that is the amount of charge that the receiver has to deal with. If we imagine that where that conic section touches the surface is a unit-area, then that whole conic section is a unit-volume. If my interpretation is correct, then that section has a volume that is equal to the volume of a sphere with 1/3rd of the radius of this sphere. So imagine that we take the sphere, create another sphere that has 1/3rd the radius, and then squash that smaller sphere into the shape of the conic section. It should match. That's all I'm trying to say about that. It seems logical to me, but am open to criticism as well.
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
Another way your picture works for me is that we can work backwards. We look at the emission radius at the receiver and project that back onto the emitter to find the actual area required by this interaction. This method does not work with my charge points because we are trying to find the charge density across the entire receiver, not at particular points on it. You could use that for a star pushing out on a planet when you just want the amount of repulsion and don't care about spins.
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
.
Maybe the charge point (N,S,E,W,F,B) method can be used for the relative case. You mentioned tracking state changes. Why not track the last 10 (or however many) state changes - and when they occurred - for each particle’s N,S,E,W,F,B cardinal locations. The past position of the emitter may then be compared to the present in order to arrive at a gravity component to the velocity or spin changes based on the change in charge received from that particle in the past.
.
Maybe the charge point (N,S,E,W,F,B) method can be used for the relative case. You mentioned tracking state changes. Why not track the last 10 (or however many) state changes - and when they occurred - for each particle’s N,S,E,W,F,B cardinal locations. The past position of the emitter may then be compared to the present in order to arrive at a gravity component to the velocity or spin changes based on the change in charge received from that particle in the past.
.
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
That is actually a reason why we can't use that method. There are too many charge interactions so it would require too much history. At 60 frames per second we would have to record 60 state changes only to have 1s worth of history because charge interactions tend to happen over many frames.
Even if we could use it though, we wouldn't need to store history for each charge point since they are just used to find the resultant velocity and spin, which is what we would store. The charge points are just a way to break up the surface that is being bombarded with charge so that we can find small differences and apply them individually. They still collectively represent the surface of the receiver and they are always put back into a single vector for velocity and a single quaternion for spin.
Maybe we could tackle it slightly differently and still use the history. Instead of recording every collision, we just sample every entity at regularly intervals and record its state. The recorded state becomes the current state minus the previous state. This makes it easier to determine how much history you will store too. Because we set the time between samples, we know the sample rate. Multiply that by the number of samples and you have the time that those samples cover.
So if we sampled every second and kept 60 state changes, then we would have 1 minute of approximate history.
However, I don't think that is to be used in this app. We are dealing with protons not planets and stars, so we don't really have a history problem.
Even if we could use it though, we wouldn't need to store history for each charge point since they are just used to find the resultant velocity and spin, which is what we would store. The charge points are just a way to break up the surface that is being bombarded with charge so that we can find small differences and apply them individually. They still collectively represent the surface of the receiver and they are always put back into a single vector for velocity and a single quaternion for spin.
Maybe we could tackle it slightly differently and still use the history. Instead of recording every collision, we just sample every entity at regularly intervals and record its state. The recorded state becomes the current state minus the previous state. This makes it easier to determine how much history you will store too. Because we set the time between samples, we know the sample rate. Multiply that by the number of samples and you have the time that those samples cover.
So if we sampled every second and kept 60 state changes, then we would have 1 minute of approximate history.
However, I don't think that is to be used in this app. We are dealing with protons not planets and stars, so we don't really have a history problem.
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
Okay, this is really fun and only slightly off-topic.
But if you load up the "Proton -> Stack 3" sim and stare at it for a bit, then look away somewhere else, your vision keep warping for a moment! Reality appears to ripple, the optics are fun. Just thought it was cool!
But if you load up the "Proton -> Stack 3" sim and stare at it for a bit, then look away somewhere else, your vision keep warping for a moment! Reality appears to ripple, the optics are fun. Just thought it was cool!
Jared Magneson- Posts : 525
Join date : 2016-10-11
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
.
Good longitude to you.
Jarred, when I stare at things like that I see auras - of course I 'm sure that's due to strictly visual persistence. On the other hand I do like thinking of auras. At first I thought it was New Age nonsense. Now, I merely find it hard to believe anyone could actually perceive our real charge field auras.
Nevyn, I must ask, using your examples, I know how to set a particle's: type; position; velocity; and orientation. I believe the only thing missing - I've made several attempts - how should I set an initial spin?
.
Good longitude to you.
Jarred, when I stare at things like that I see auras - of course I 'm sure that's due to strictly visual persistence. On the other hand I do like thinking of auras. At first I thought it was New Age nonsense. Now, I merely find it hard to believe anyone could actually perceive our real charge field auras.
Nevyn, I must ask, using your examples, I know how to set a particle's: type; position; velocity; and orientation. I believe the only thing missing - I've made several attempts - how should I set an initial spin?
.
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
Page 3 of 15 •  1, 2, 3, 4 ... 9 ... 15
1, 2, 3, 4 ... 9 ... 15 
 Similar topics
Similar topics» Particle Drifts in Space
» Modeling a Charge Particle
» Spinning Particle Language
» The First Ever Photograph of Light as both a Particle and Wave
» Physicists Finally Narrowed Down the Mass of the Tiniest 'Ghost Particle' in the Universe
» Modeling a Charge Particle
» Spinning Particle Language
» The First Ever Photograph of Light as both a Particle and Wave
» Physicists Finally Narrowed Down the Mass of the Tiniest 'Ghost Particle' in the Universe
Page 3 of 15
Permissions in this forum:
You cannot reply to topics in this forum