Simple Orbiter 2
5 posters
Page 2 of 2
Page 2 of 2 •  1, 2
1, 2
 Still no Angular Momentum
Still no Angular Momentum
.
I posted a gif of Boids showing a few slow bounces, elsewhere here recently, Re: Stacked Spins - scripting the photon's motion (technical), https://milesmathis.forumotion.com/t278p75-stacked-spins-scripting-the-photon-s-motion-technical#2915. It belongs here.
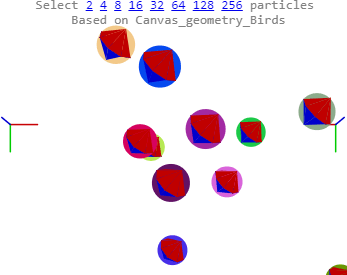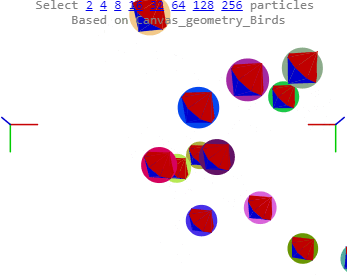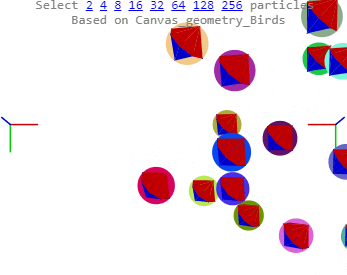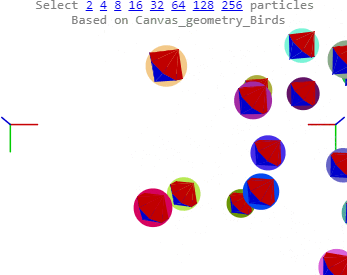
The spins aren’t included yet. I’ll make this a review and update with pretty new pictures.

Two positive spheres, magenta and green, with equal mass and length radii, traveling linearly in the direction of the spin axis (perfect spirals makes the example slightly simpler) in roughly opposing directions happen to meet. Each sphere contributes two direction/velocity vectors: 1) a Forward linear velocity - here, green or magenta - gF or mF; and 2) the tangential spin velocity at the collision Latitude - gL or mL. The gL and mL tangent velocity vectors are shown with their latitude sources.

The two tangential vectors gL and mL form the collision plane. Their cross product describes the perpendicular direction between the two colliding sphere centers. One must be able to determine whether angular exchange leads to a change in the spin rates or cause torque and precession – an adjustment to the forward direction - or if at light speed, begin an x spin tumble.
The gif shows that the bounce works. I’m still stuck at angular momentum - yes, going in circles. Oh, and programming – call that the lack of. Over the last two weeks I’ve enjoyed viewing many new three.js examples and updating from version 61 to 87 something, something permanent brain damage.
.
I posted a gif of Boids showing a few slow bounces, elsewhere here recently, Re: Stacked Spins - scripting the photon's motion (technical), https://milesmathis.forumotion.com/t278p75-stacked-spins-scripting-the-photon-s-motion-technical#2915. It belongs here.

The spins aren’t included yet. I’ll make this a review and update with pretty new pictures.

Two positive spheres, magenta and green, with equal mass and length radii, traveling linearly in the direction of the spin axis (perfect spirals makes the example slightly simpler) in roughly opposing directions happen to meet. Each sphere contributes two direction/velocity vectors: 1) a Forward linear velocity - here, green or magenta - gF or mF; and 2) the tangential spin velocity at the collision Latitude - gL or mL. The gL and mL tangent velocity vectors are shown with their latitude sources.

The two tangential vectors gL and mL form the collision plane. Their cross product describes the perpendicular direction between the two colliding sphere centers. One must be able to determine whether angular exchange leads to a change in the spin rates or cause torque and precession – an adjustment to the forward direction - or if at light speed, begin an x spin tumble.
The gif shows that the bounce works. I’m still stuck at angular momentum - yes, going in circles. Oh, and programming – call that the lack of. Over the last two weeks I’ve enjoyed viewing many new three.js examples and updating from version 61 to 87 something, something permanent brain damage.
.
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
 Re: Simple Orbiter 2
Re: Simple Orbiter 2
Great work, Airman. Keep it up. Don't worry about the programming. The only thing that matters is that it works! A programming language is just a tool like any other. It serves you. Experience brings finesse, but it is not required to get results.
 Re: Simple Orbiter 2
Re: Simple Orbiter 2
.
Thanks guys, no final conclusions yet. I'll need to dig deeper into the subject.
Nevyn have you made any progress studying gyroscopic math? Here's a picture with a couple of concerns.

Any comments are welcome.
.
Thanks guys, no final conclusions yet. I'll need to dig deeper into the subject.
Nevyn have you made any progress studying gyroscopic math? Here's a picture with a couple of concerns.

Any comments are welcome.
.
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
 Re: Simple Orbiter 2
Re: Simple Orbiter 2
I don't know about precession rotating about the collision point, but it seems that Miles said or implied that the higher level spin rotates around that point.
LloydK- Posts : 548
Join date : 2014-08-10
 Re: Simple Orbiter 2
Re: Simple Orbiter 2
I haven't looked at it in some time. The collision point is either the new point of rotation (for the new top spin level) or it is on the opposite side from that if you draw a line between the centers of the colliding particles. I lean towards the former, just because it is a real point where-as the other one is a bit more of a virtual point (as it might not even be on the BPhoton). On the other hand, that collision point is where we need to attach the new tangential velocity vector, which is not the same as the rotation point. So I like both for different reasons. Which is more real: the rotation point or the velocity point? When asked like that, I lean towards the velocity.
Reality is probably even trickier and something else entirely.
That doesn't help much, does it?
Maybe we need to work it in both directions and take the path of least resistance. That is, which one is easier to work with and calculate.
Reality is probably even trickier and something else entirely.
That doesn't help much, does it?
Maybe we need to work it in both directions and take the path of least resistance. That is, which one is easier to work with and calculate.
 Re: Simple Orbiter 2
Re: Simple Orbiter 2
When we study this, should we take into account the constant speed of light?
Ciaolo- Posts : 143
Join date : 2016-09-08
 Update
Update
.
Alrighty already, here's an update. I've spent most of my quality time during the last couple of weeks relearning and cleaning up Boids, I'm still very much a beginner. I removed all but a mention or two of the original bird flocking functions, such as wall avoidance. I admit I tend to include anything understood or not that can be reused or modified and am generally a slob. I apologize for having shared such a mess. In my defense, I’m concentrating on vectors. I’ve worked plenty of problems with matrices before, certainly in my Linear Algebra class (shudder) and others. One can easily read the scale, translation, rotation and more in a change matrix. I’m limiting myself to a straight vector solution if at all possible. The Euler axis/angle operation is perfectly acceptable.
I believe it’s fair to say I’m trying to model A-spin particle collisions at velocities well below light speed, but there are too many unknowns. I’m working with a given modeling space without a defined radius. It’s relatively confusing. For a given velocity - below c - the smaller the radius, the faster the particle. Each particle contributes gravity and charge inversely - the smaller the particle, the stronger the charge and weaker the gravity. At the smallest radius, photons do not emit charge and fly in straight lines, interrupted only by the occasional photon collision. Larger charged particles are subject to continuous charge accelerations and may travel in curved trajectories.
The model seems to match that, I can watch particles interact in complex loops or reduce or turn off the accelerations, leaving the particles simply bouncing in straight lines within a box, wraparound space or work out something else. I would implement the radius/tangential relationship Nevyn has written about; maybe we can tie gravity or charge magnitudes to the radius/spin frequency relationship. It’s just a tiny model but I would guess working with the magnitude scale changes between charged particles with any model would bring similar problems.
I agree that any collision precession below the speed of light would occur around the collision point, but then, in a collision, how can two simultaneous rotations precess around the same point independently? I appreciate the question between the collision center and center of the X-spin, again, precession is somehow involved. I agree that the top spin tangential or linear velocities of a particle (including a photon) can be much less than c, the X rotation may start off slow.
I'm still reviewing, but most of the collision vectors are drafted and ready. My immediate goal moving ahead with angular momentum is a wall bounce. Given a ball’s velocity, mass, composition, radius, surface friction, elasticity, gravity, etc., we are told that the angle of incidence equals the angle of reflection. That’s easily shown to be wrong when spin is involved. How exactly does spinning effect the bounce? I’m still not sure, since it involves some non-intuitive results. I’ll again refer you to Richard L. Garwin’s, “Kinematics of an Ultraelastic Rough Ball” *. The ultraelastic superball bounce is what I’ll shoot for. I have no problem accepting bounces since it seems to me that a particle bounce is equivalent to collision with the particle’s reflection - an anti-particle.
* The American Journal of Physics, vol. 37, no. 1, January 1969, Kinematics of an Ultraelastic Rough Ball http://www.rpi.edu/dept/phys/courses/PHYS1150/GarwinSuperBall.pdf
.
Alrighty already, here's an update. I've spent most of my quality time during the last couple of weeks relearning and cleaning up Boids, I'm still very much a beginner. I removed all but a mention or two of the original bird flocking functions, such as wall avoidance. I admit I tend to include anything understood or not that can be reused or modified and am generally a slob. I apologize for having shared such a mess. In my defense, I’m concentrating on vectors. I’ve worked plenty of problems with matrices before, certainly in my Linear Algebra class (shudder) and others. One can easily read the scale, translation, rotation and more in a change matrix. I’m limiting myself to a straight vector solution if at all possible. The Euler axis/angle operation is perfectly acceptable.
I believe it’s fair to say I’m trying to model A-spin particle collisions at velocities well below light speed, but there are too many unknowns. I’m working with a given modeling space without a defined radius. It’s relatively confusing. For a given velocity - below c - the smaller the radius, the faster the particle. Each particle contributes gravity and charge inversely - the smaller the particle, the stronger the charge and weaker the gravity. At the smallest radius, photons do not emit charge and fly in straight lines, interrupted only by the occasional photon collision. Larger charged particles are subject to continuous charge accelerations and may travel in curved trajectories.
The model seems to match that, I can watch particles interact in complex loops or reduce or turn off the accelerations, leaving the particles simply bouncing in straight lines within a box, wraparound space or work out something else. I would implement the radius/tangential relationship Nevyn has written about; maybe we can tie gravity or charge magnitudes to the radius/spin frequency relationship. It’s just a tiny model but I would guess working with the magnitude scale changes between charged particles with any model would bring similar problems.
I agree that any collision precession below the speed of light would occur around the collision point, but then, in a collision, how can two simultaneous rotations precess around the same point independently? I appreciate the question between the collision center and center of the X-spin, again, precession is somehow involved. I agree that the top spin tangential or linear velocities of a particle (including a photon) can be much less than c, the X rotation may start off slow.
I'm still reviewing, but most of the collision vectors are drafted and ready. My immediate goal moving ahead with angular momentum is a wall bounce. Given a ball’s velocity, mass, composition, radius, surface friction, elasticity, gravity, etc., we are told that the angle of incidence equals the angle of reflection. That’s easily shown to be wrong when spin is involved. How exactly does spinning effect the bounce? I’m still not sure, since it involves some non-intuitive results. I’ll again refer you to Richard L. Garwin’s, “Kinematics of an Ultraelastic Rough Ball” *. The ultraelastic superball bounce is what I’ll shoot for. I have no problem accepting bounces since it seems to me that a particle bounce is equivalent to collision with the particle’s reflection - an anti-particle.
* The American Journal of Physics, vol. 37, no. 1, January 1969, Kinematics of an Ultraelastic Rough Ball http://www.rpi.edu/dept/phys/courses/PHYS1150/GarwinSuperBall.pdf
.
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
 Another possible bounce
Another possible bounce
.
The latest. Another possible bounce.
Garwin’s ultraelastic rough ball bounce analysis above is limited to either the normal (perpendicular to the collision) or to the forward horizontal direction parallel to the collision. Ignoring details such as slip, slide or grip regimes, the forward direction includes the horizontal component of the forward motion as well as the ball’s equatorial spin tangential surface velocity, assumed parallel to the ball’s forward motion (as in rolling, top or bottom spin). I was left to speculate how Garwin might treat a more complicated case, and so came to focus on the collision vectors expressed either perpendicular or parallel to the ball’s spin axis; in which case any reflected deviation from the incident angle would be due to precession. But that would mean every particle loses energy with every bounce, as high velocities are converted to spin axis reorientations. Stuck again, but not idle, my mind flips between bounces and collisions regularly.
I went back through the papers looking for additional reference sources, and found a promising title - A classical experiment revisited: The bounce of balls and superballs in three dimensions. Am. J. Phys. 73, 28-36, 2005. I ended up at Research Gate requesting the paper. First thing Monday, I found the author, Antonio Doménech, had graciously e-mailed me a copy. I was immediately struck by the paper’s bounce schematic, again, very promising.

Vo, the hypotenuse vector on the left, is the ball’s initial velocity vector. Vo = Voz + Vox . Voz is related to the normal force Fn, the linear or vertical component of the bounce. The main collision component is Vox, the forward motion’s horizontal component, which will feel a frictional resistance of Ffx. The arbitrary spin of the ball is described by three rotations omega-x, omega-y, omega-z. Voy, has been added to account for the arbitrary spin – amounting to a y component of the ball’s tangential surface velocity just before contact; Voy is countered by the frictional force Ffy. The rebound vector is V. V = Vx + Vy + Vz.
The paper provides two fairly direct and simple sets of formulas in order to determine rebound for two different types of balls. Experiments were conducted to determine how well the two models predicted the outcome. Easy, right? Sorry, no; it’s not at all clear to me how one resolves an arbitrary spin into orthogonal x,y and z frequency components. Sounds like I'll need to include Euler angles.

Here’s the vector diagram (leaving out the angles for simplicity) when I bring in the latitudinal tangential spin velocity, Vs. Vs = Vsx + Vsy . Ffx must now counter Vox plus Vsx ; Ffy must counter Vsy . It’s not the form given in the paper, but it seems easy enough to try.
P.S. The vector lengths don't add in the image. I didn't want to lay Vsx on top of Ffx. Ffx is actually much shorter than shown since Vox and Vsx mostly cancel.
.
The latest. Another possible bounce.
Garwin’s ultraelastic rough ball bounce analysis above is limited to either the normal (perpendicular to the collision) or to the forward horizontal direction parallel to the collision. Ignoring details such as slip, slide or grip regimes, the forward direction includes the horizontal component of the forward motion as well as the ball’s equatorial spin tangential surface velocity, assumed parallel to the ball’s forward motion (as in rolling, top or bottom spin). I was left to speculate how Garwin might treat a more complicated case, and so came to focus on the collision vectors expressed either perpendicular or parallel to the ball’s spin axis; in which case any reflected deviation from the incident angle would be due to precession. But that would mean every particle loses energy with every bounce, as high velocities are converted to spin axis reorientations. Stuck again, but not idle, my mind flips between bounces and collisions regularly.
I went back through the papers looking for additional reference sources, and found a promising title - A classical experiment revisited: The bounce of balls and superballs in three dimensions. Am. J. Phys. 73, 28-36, 2005. I ended up at Research Gate requesting the paper. First thing Monday, I found the author, Antonio Doménech, had graciously e-mailed me a copy. I was immediately struck by the paper’s bounce schematic, again, very promising.

Vo, the hypotenuse vector on the left, is the ball’s initial velocity vector. Vo = Voz + Vox . Voz is related to the normal force Fn, the linear or vertical component of the bounce. The main collision component is Vox, the forward motion’s horizontal component, which will feel a frictional resistance of Ffx. The arbitrary spin of the ball is described by three rotations omega-x, omega-y, omega-z. Voy, has been added to account for the arbitrary spin – amounting to a y component of the ball’s tangential surface velocity just before contact; Voy is countered by the frictional force Ffy. The rebound vector is V. V = Vx + Vy + Vz.
The paper provides two fairly direct and simple sets of formulas in order to determine rebound for two different types of balls. Experiments were conducted to determine how well the two models predicted the outcome. Easy, right? Sorry, no; it’s not at all clear to me how one resolves an arbitrary spin into orthogonal x,y and z frequency components. Sounds like I'll need to include Euler angles.

Here’s the vector diagram (leaving out the angles for simplicity) when I bring in the latitudinal tangential spin velocity, Vs. Vs = Vsx + Vsy . Ffx must now counter Vox plus Vsx ; Ffy must counter Vsy . It’s not the form given in the paper, but it seems easy enough to try.
P.S. The vector lengths don't add in the image. I didn't want to lay Vsx on top of Ffx. Ffx is actually much shorter than shown since Vox and Vsx mostly cancel.
.
Last edited by LongtimeAirman on Wed Oct 25, 2017 8:41 pm; edited 2 times in total (Reason for editing : Added PS)
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
 Stuck at the Controls
Stuck at the Controls
.
Sorry, no oblique bounce progress to report. I wish I could say I’ve been taking a break; instead, I’ve been tied up in Threejs, JavaScript and HTML controls, every day, many hours since my last post. I’ve been studying the subject and tinkering with the program. My understanding has improved, but not well enough, I’m afraid of dropping dead before it’s done.
Nevyn, Please help. I hope you don’t mind the imposition, I’m still embarrassed from last time. I have every intention of improving this project and I’m otherwise extremely happy with it. There’s plenty of opportunity to work with the physics and the faster we can come up with an acceptable product the better to explore collisions in detail. Ideally, eventually, I hope you see fit to adopt it, and include it on your site, unless of course you’ve created your own collision model. In any case, please don’t hesitate to do your best on my account.
As you know, most of the code for this GravityAndChargeFieldDemo (Boids) started as canvas_geometry_birds, https://threejs.org/examples/#canvas_geometry_birds (c_g_t ) - just flocking birds, no control keys required. I modified c_g_t by copying the HTML hash control for the number of particles from webgl_gpgpu_birds, https://threejs.org/examples/#webgl_gpgpu_birds, (w_g_b). w_g_b makes very little sense to me.
There are several other variables in Boids: scale (or particle radius), wallBounce or wraparound, various grids, and particle appearance (sprites or marbles). I change those variables from inside the .html file. That’s unacceptable, so I’ve been trying to add user controls.
I’ve begun to copy the set of HTML controls from https://threejs.org/examples/#webgl_geometry_text, (w_g_t), but the hashtable/control structure has frustrated the beegeebers out of me.
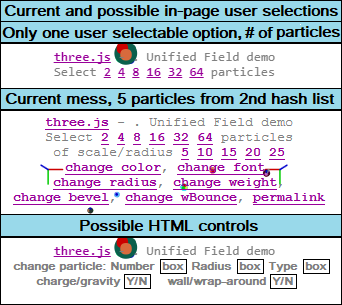
I haven’t made any progress in dat.gui.min.js controls either, since the mousedrag event belongs to the OrbitControls camera. I cannot adjust a slider – the scene moves instead. I suppose the dat.gui could work if it were limited to just buttons and not slide bars. A possible fix -
Sending the code in a separate pm.
.
Sorry, no oblique bounce progress to report. I wish I could say I’ve been taking a break; instead, I’ve been tied up in Threejs, JavaScript and HTML controls, every day, many hours since my last post. I’ve been studying the subject and tinkering with the program. My understanding has improved, but not well enough, I’m afraid of dropping dead before it’s done.
Nevyn, Please help. I hope you don’t mind the imposition, I’m still embarrassed from last time. I have every intention of improving this project and I’m otherwise extremely happy with it. There’s plenty of opportunity to work with the physics and the faster we can come up with an acceptable product the better to explore collisions in detail. Ideally, eventually, I hope you see fit to adopt it, and include it on your site, unless of course you’ve created your own collision model. In any case, please don’t hesitate to do your best on my account.
As you know, most of the code for this GravityAndChargeFieldDemo (Boids) started as canvas_geometry_birds, https://threejs.org/examples/#canvas_geometry_birds (c_g_t ) - just flocking birds, no control keys required. I modified c_g_t by copying the HTML hash control for the number of particles from webgl_gpgpu_birds, https://threejs.org/examples/#webgl_gpgpu_birds, (w_g_b). w_g_b makes very little sense to me.
There are several other variables in Boids: scale (or particle radius), wallBounce or wraparound, various grids, and particle appearance (sprites or marbles). I change those variables from inside the .html file. That’s unacceptable, so I’ve been trying to add user controls.
I’ve begun to copy the set of HTML controls from https://threejs.org/examples/#webgl_geometry_text, (w_g_t), but the hashtable/control structure has frustrated the beegeebers out of me.

I haven’t made any progress in dat.gui.min.js controls either, since the mousedrag event belongs to the OrbitControls camera. I cannot adjust a slider – the scene moves instead. I suppose the dat.gui could work if it were limited to just buttons and not slide bars. A possible fix -
I don't see how to apply it. I suppose my control variables aren't set up properlyIf you use a mouse-controlled camera with the dat.gui.min control panel, you have to comment the following line in the MouseListener of the mouseDown action - event.preventDefault();
Sending the code in a separate pm.
.
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
 Re: Simple Orbiter 2
Re: Simple Orbiter 2
Do you want me to add controls to manipulate those values? I can do that and document it more thoroughly than I normally would so that you can see what is going on and how to add to and alter it yourself (along with a bit of research, probably). I will use basic HTML/JS code at first. Later, when you are comfortable with that, I can show you how to make it look prettier with little change (just the controls, it won't change the ThreeJS parts).
I will look over the physics as well and see how it lines up with my own thoughts on the subject.
I will look over the physics as well and see how it lines up with my own thoughts on the subject.
 Re: Simple Orbiter 2
Re: Simple Orbiter 2
.
Thanks Nevyn, yes, just add additional controls so anyone can change them, that would be great.
I'm still worried whether you see it operating properly or not. I may need to explain a variable or two.
In the diagram I show (box). (box) can be a pull down list.
I'd like to discuss any physics objections you may have, or at least give my understanding. I've provided plenty of comments. There are factorial numbers of accelerations/calculations going on, the program is a pig, but it's a pretty pig.
.
Thanks Nevyn, yes, just add additional controls so anyone can change them, that would be great.
I'm still worried whether you see it operating properly or not. I may need to explain a variable or two.
In the diagram I show (box). (box) can be a pull down list.
I'd like to discuss any physics objections you may have, or at least give my understanding. I've provided plenty of comments. There are factorial numbers of accelerations/calculations going on, the program is a pig, but it's a pretty pig.
.
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
Page 2 of 2 •  1, 2
1, 2
Page 2 of 2
Permissions in this forum:
You cannot reply to topics in this forum