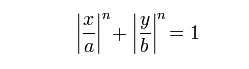Pi with Radians

I have an open question on this. While I've always recognized π as 3.14xxx. I found the picture above interesting in that a perpendicular line is set for marking "π" and 2π" for a non-real number (endless essentially).



http://en.wikipedia.org/wiki/Radian

------

Use in physics

The radian is widely used in physics when angular measurements are required. For example, angular velocity is typically measured in radians per second (rad/s). One revolution per second is equal to 2π radians per second.

Similarly, angular acceleration is often measured in radians per second per second (rad/s2).

For the purpose of dimensional analysis, the units are s−1 and s−2 respectively.

Likewise, the phase difference of two waves can also be measured in radians. For example, if the phase difference of two waves is (k·2π) radians, where k is an integer, they are considered in phase, whilst if the phase difference of two waves is (k·2π + π), where k is an integer, they are considered in antiphase.

Multiples of radian units

Metric prefixes have limited use with radians, and none in mathematics. A milliradian (mrad) is a thousandth of a radian and a microradian (urad or μrad) is a millionth of a radian, i.e. 103 mrad = 106 urad = 1 rad.

There are 2π × 1000 milliradians (≈ 6283.185 mrad) in a circle. So a trigonometric milliradian is just under 1⁄6283 of a circle. This “real” trigonometric unit of angular measurement of a circle is in use by telescopic sight manufacturers using (stadiametric) rangefinding in reticles. The divergence of laser beams is also usually measured in milliradians.

An approximation of the trigonometric milliradian (0.001 rad), known as the (angular) mil, is used by NATO and other military organizations in gunnery and targeting. Each angular mil represents 1⁄6400 of a circle and is 1-⅞% smaller than the trigonometric milliradian. For the small angles typically found in targeting work, the convenience of using the number 6400 in calculation outweighs the small mathematical errors it introduces. In the past, other gunnery systems have used different approximations to 1⁄2000π; for example Sweden used the 1⁄6300 streck and the USSR used 1⁄6000. Being based on the milliradian, the NATO mil subtends roughly 1 m at a range of 1000 m (at such small angles, the curvature is negligible).

Smaller units like microradians (μrad) and nanoradians (nrad) are used in astronomy, and can also be used to measure the beam quality of lasers with ultra-low divergence. More common is arc second, which is π⁄648,000 radians (around 4.8481 microradians). Similarly, the prefixes smaller than milli- are potentially useful in measuring extremely small angles.

Cr6 wrote:I have an open question on this. While I've always recognized π as 3.14xxx. I found the picture above interesting in that a perpendicular line is set for marking "π" and 2π" for a non-real number (endless essentially).

Chromium, I would like to discuss, but I don't understand your "open question". The only numbers I see 'above' are 1 and π.

LongtimeAirman wrote:

Cr6 wrote:I have an open question on this. While I've always recognized π as 3.14xxx. I found the picture above interesting in that a perpendicular line is set for marking "π" and 2π" for a non-real number (endless essentially).

Chromium, I would like to discuss, but I don't understand your "open question". The only numbers I see 'above' are 1 and π.

Hi LTAM,

I was looking at the top most animated .gif graphic where the wheel rotates. The vertical line is set to mark off an irrational number i.e, π. Just always found that graphic curious with the line markings that's all.

Update from Mathis' new paper: The Cycloid and the Kinematic Circumference

www.milesmathis.com/cycloid.pdf

A Cycloid.

https://en.wikipedia.org/wiki/Cycloid

If a cycloid is mirrored at the base, is the resulting shape an ellipse? If so, what is the relation between this ellipse and the circle used to construct the cycloid?

Good questions Ciaolo. Maybe we can start with the hyperellipse.
From:
http://www.clemson.edu/economics/faculty/wilson/R-tutorial/toc.html
http://www.clemson.edu/economics/faculty/wilson/R-tutorial/graphics.html

5.2 Plotting Shapes (as Opposed to Functions)
The previous examples involved plotting univariate functions, which are unique mappings. Sometimes, however, we wish to plot shapes that do not involve unique mappings. As an example, consider Lamé curves. A Lamé curve is a geometric figure defined in the Cartesian coordinate system as the set of all points (x, y) with

where n, a and b are positive numbers.This formula defines a closed curve contained in the rectangle -a ? x ? +a and -b ? y ? +b. The parameters a and b are called the semi-diameters of the curve. When n is between 0 and 1, the superellipse looks like a four-armed star with concave (inwards-curved) sides. For n = 1/2, in particular, the sides are arcs of parabolas. When n is 1 the curve is a diamond with corners (±a, 0) and (0, ±b). When n is between 1 and 2, it looks like a diamond with those same corners but with convex sides. The curvature increases without limit as one approaches the corners.
When n is 2, the curve is an ordinary ellipse (in particular, a circle if a = b). When n is greater than 2, it looks superficially like a rectangle with chamfered (rounded) corners. The curvature is zero at the points (±a, 0) and (0, ±b).
If n < 2 the figure is also called an hypoellipse; if n > 2, a hyperellipse. When n = 1 and a = b, the superellipse is the boundary of a ball of R2 in the n-norm.
The following R code will plot a hyperellipse:
> a=3.75
> b=1.5
> n=3
> x=seq(0,a,0.01)
> y=b*(1-(x/a)**n)**(1/n)
> plot(x,y,type='l',xlim=c(-a,a),ylim=c(-a,a))
> lines(x,-y)
> lines(-x,-y)
> lines(-x,y)

Just find the right a and b.
.
Forgive me. I'm trying to learn R.
.

Obviously a is the diameter and b is half the circumference of the circle that producted the cycloid. We must find n.

Thanks Ciaolo.

I played with a=pi, b=2 and various n's, n=2 looked best. I'm certain I'm leading us astray.

Lamé Cartesian equation:
(x/a)^n + (y/b)^n = 1
Cycloid Parametric Cartesian equation:
x = at - h sin(t), y = a - h cos(t)

They are very different. As we now know, we have historically confused a diagram of a curve, say a circle or an ellipse - with circular motion, as with say an orbit, or a cycloid. An important part of Miles' latest Pi update and Cycloid papers point to the fact that kinematic motion requires time while diagrams do not. He's turned me upside down so often I not sure which right now.

How does that affect your question - What is the relation between this ellipse and the circle used to construct the cycloid?
.

The mirrored cycloid does produce an ellipse with a short axis equal to the diameter of the circle and a long axis equal to half of the geometric circumference.

Equation for Ellipse:
(x^2/a^2) + (y^2/b^2) = 1

a is the x-radius (long)
b is the y-radius (short)

Therefore the cycloid ellipse is found by:
Let:
a = 2*pi*r/2 = pi*r
b = 2r
Then:
(x^2/a^2) + (y^2/b^2) = 1
=> (x^2/(pi*r)^2) + (y^2/(2r)^2) = 1

Let's take the ratio of the radii:
a/b = pi*r / 2r = pi/2

The long axis is pi/2 times longer than the length of the short one.

Area of Ellipse = pi*a*b
=> pi * pi*r * 2r
=> pi^2 * 2r^2
=> 2(pi*r)^2
=> pi*r^2 * 2pi

Area of Circle = pi*r^2

Ratio of ellipse to circle = (pi*a*b) / (pi*r*r)
=> (pi^2 * 2r^2) / (pi*r^2)
=> pi*2
=> 2pi

The ellipse has 2pi times the area of the original circle.

Therefore the cycloid has pi times the area of the circle.

Do we need to think about kinematic area and volume? I think my head is about to explode!

.
Nevyn, "I think my head is about to explode!" Thanks for the warning, it gave me time to shut my mouth.
.

The ratio between circle and cycloid is pi. That is very interesting, don't you think?
But are we sure that the cycloid and the semi-ellipse have the same shape? We need some CAD program to draw them...

Thank you for the answers

EDIT: I forgot, what about the eclipse focii positions, the circumference points they were and their radians?
Aren't you curious about this?

Ciaolo, Is this what you want? Are there any lines you would like added, aside of course from a superposition with the cycloid. Just keep in mind that the line segment lengths change over the course of the cycloid creation. There is no such concern in ellipses. We may be trying to compare apples and oranges.

The focal points are found using this equation:
F = sqrt( a^2 - b^2 )
Let:
a = pi*r
b = 2r
Then:
F = sqrt( (pi*r)^2 - (2r)^2 )
=> F = sqrt( pi^2 * r^2 - 4r^2 )
=> F = sqrt( (r^2)( pi^2 - 4 ) )
=> F = sqrt( (r^2)(pi-2)(pi+2) )  // these 2 steps are not necessary
=> F = sqrt( r^2 * 1.14 * 5.14 ) // I was trying to find another way to express it
=> F = sqrt( r^2 * 5.87 )
=> F = 2.42r

I couldn't find another way to express 2.42 so this doesn't seem as interesting as the previous findings.

While the cycloid is created, there are 2 points on it where the center of the circle intersects with it. Could it be that these points projected to the base give us the location of the ellipse focii? I don't know how to calculate that...

LongtimeAirman, I know that the nature of the two shapes is different, but they can be drawn and observed.

.
I tried to add title and such without success so far. The circles that create the two mirror cycloids roll along the y=0 line. The circle centers will always lie on y = +/- 1. The focii are marked.

Equation for Ellipse:
(x^2/a^2) + (y^2/b^2) = 1
=> (x^2/a^2) = 1 - (y^2/b^2)
=> x^2 = a^2 * (1 - y^2/b^2)
=> x = sqrt( a^2 * (1 - y^2/b^2) )
=> x = a * sqrt( 1 - y^2/b^2 )
=> y = b * sqrt( 1 - x^2/a^2 )

The center of the circle touches the cycloid line when y equals the radius.

Let:
x = a * sqrt( 1 - y^2/b^2 )
y = r
a = pi*r
b = 2r
Then:
x = pi*r * sqrt( 1 - r^2/(2r)^2 )
x = pi*r * sqrt( 1 - 1/4 )
x = pi*r * sqrt( 3/4 )
x = 2.72r from the center of the ellipse

The cycloid starts when x = pi*r

x = pi*r - 2.72r
 = r(pi - 2.72)
 = 0.42r from the start of the cycloid

The length of the geometric circumference that is inside of those points is 2 * 2.72r = 5.44r.

In order to determine if the mirrored cycloid is the same as our ellipse we can compare their lengths.

Calculating the circumference of an ellipse is not easy but we can get a close approximation with the following formula.

h = (a-b)^2 / (a+b)^2
p = pi(a+b)(1 + 1/4 * h + 1/64 * h^2 + 1/256 * h^3)

Let:
a = pi*r
b = 2r
r = 1
Then:
a = pi
b = 2
h = (a-b)^2 / (a+b)^2
 = (pi-2)^2 / (pi+2)^2
 = 1.303 / 26.436
 = 0.049
p = pi(a+b)(1 + 1/4 * h + 1/64 * h^2 + 1/256 * h^3)
 = pi(pi+2)(1 + 0.049/4 + (0.049^2)/64 + (0.049^3)/256)
 = pi(pi+2)(1 + 0.012 + 3.797e-5 + 4.679e-7)
 = pi(pi+2)(1.012)
 = 16.352

p is the full circumference of the ellipse so we just halve it to get a value to compare to the length of the cycloid.

p/2 = 16.352/2
   = 8.176

The length of the cycloid is 8r, r=1 so the length is 8.
Not an exact match but we couldn't find the exact circumference of the ellipse. Close enough, I think. I would have felt a little bit better if p was slightly below 16 since calculating p requires an infinite sum of terms and each term is adding so it will make the value slightly larger the more terms we use. This probably tells us that the cycloid does not quite match the ellipse.

It could also be telling us that there is a more exact way to calculate the circumference of an ellipse and we haven't found it yet. The equation I used is said to be exact, if calculated to an infinite sum (how does one do that exactly?) and the terms start to get very small very quickly so the value I calculated is quite close, according to that equation. The cycloid seems too close to an ellipse for it not to be one. I don't know much about ellipses, though. Maybe it is a special type.

Sorry guys. I've thrown you a curve-ball. I should have done more research.

Equation of Cycloid:

th = theta = angle from point to circle center to surface circle is rolling on
x = r(th - sin(th))
y = r(1 - cos(th))

If:
th = pi/2
Then:
x = r(pi/2 - sin(pi/2))
= r(pi/2 - 1)
= 0.57r
y = r(1 - cos(pi/2))
= r(1 - 0)
= r

When the center of the circle touches the cycloid, it has traveled 0.57r which is not equal to the 0.42r I calculated above. Therefore, the cycloid does not make an ellipse or it is to be considered a special type of ellipse.

To find the point from the center of the cyclipse (cycloid-ellipse) we subtract the x equation above from half the geometric circumference.

(pi * r) - r(pi/2 - sin(pi/2))
= r( pi - (pi/2 - sin(pi/2))
= r( pi - pi/2 + sin(pi/2))
= r(pi/2 + sin(pi/2))
= r(pi/2 + 1)
= 2.57r

Which is not equal to the 2.72r calculated in my previous post.

This is turning into a first R script.

I created an ellipse function with default variables making studying easier.  
# ellipse <- function(a = pi, b = 2, n = 2) {
#   y<-b*(1-(x/a)**n)**(1/n)
#   plot(x,y,type='l',xlim=c(-a,a),ylim=c(-b,b))
#   lines(x,-y)
#   lines(-x,-y)
#   lines(-x,y)
# }

Here are the two curves, showing just half the ellipse to emphasizing any difference. As you can see, with n=2, the ellipse does not match the cycloid.

Code:

# EllipseVsCycloid
> a<-pi
> b<-2
> n<-2
> y<-b*(1-(x/a)**n)**(1/n)
> plot(-x,y,type='l',xlim=c(-a,a),ylim=c(0,b))
> lines(x,y)
> # The half ellipse is shown

> r<-1
> th <- seq(0,2*pi,0.05)
> xpos <- r*(th - sin(th)) - pi
> ypos <- r*(1 - cos(th))
> lines(xpos,ypos,type='l', col="red")
> # Now we can cee the cycloid
> title(main="Comparing a cycloid (red) to half an ellipse (black)")

.

Here we can see 4 different n value ellipses. The jpg image's red comes out poorly. I added the text in paint.
I would point out that n=1.75 and n=1.8, both cross the cycloids' path. That tells me the shape of the cycloid is not parabolic.

Code:


cycloid <- function(r=1){
  th <- seq(0,2*pi,0.05)
  xpos <- r*(th - sin(th)) - pi
  ypos <- r*(1 - cos(th))
  plot(xpos,ypos,type='l',xlim=c(-a,a),ylim=c(0,b), col="red")
}

addnellipsearc <- function(a = pi, b = 2, n = 2) {
  y<-b*(1-(x/a)**n)**(1/n)
  lines(x,y,type='l',xlim=c(-a,a),ylim=c(0,b))
  lines(-x,y)
}


Note. The constants that are assigned to the functions are the defaults. When you call the function include your desired constant.
.

Looking good LTAM.

Hi Cr6, Thanks. Please feel free to make any suggestions.

I just stumbled upon this one. If anyone needs further, more detailed CAD on this or animation, let me get back up to speed and I'll launch into it. Perhaps Maya and Rhino will help us understand this even better, and we can animate it too.