Simple Orbiter 2
5 posters
Page 1 of 2
Page 1 of 2 • 1, 2 
 Re: Simple Orbiter 2
Re: Simple Orbiter 2
Hey Guys, I’m still fully occupied with boids. Also studying webgl_gpgpu_birds. I’ve got a control panel (but no variables hooked up to it)! Notes with spins, collisions, and close interactions; relating angular versus linear motion. Still wobbly.

This plot is supposed to show the line-of-sight repulsion given Gravity and Charge. I’ve been treating my boids as point objects, but if my object is actually on the order of 1 (whatever unit), then the boid’s unified field is still dominated by gravity (?). Largeaccelerations velocities can be generated by a nearby boid’s gravity alone.
I guess that when we work with same scale objects – say a large number of equally sized boids, there really isn’t a balance point between gravity and charge. The balance is more between boid velocity and gravity. For the moment, it seems to me we need very large along with very small, so that the balance point will be located outside the largest object.
.

This plot is supposed to show the line-of-sight repulsion given Gravity and Charge. I’ve been treating my boids as point objects, but if my object is actually on the order of 1 (whatever unit), then the boid’s unified field is still dominated by gravity (?). Large
I guess that when we work with same scale objects – say a large number of equally sized boids, there really isn’t a balance point between gravity and charge. The balance is more between boid velocity and gravity. For the moment, it seems to me we need very large along with very small, so that the balance point will be located outside the largest object.
.
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
 Re: Simple Orbiter 2
Re: Simple Orbiter 2
Nice work with the framework and the boids LTAM. I'm really "awed" you've come this far this fast. 
 Re: Simple Orbiter 2
Re: Simple Orbiter 2
Hi Cr6, Thanks, but Nevyn told me to start studying Java last year. Actually, I’ve always been here and now. One of those divine moments. I’m stuck.
Periapsis, that moment when the charge field’s relative influence is maximum. Normally, the spin axis acts gyroscopically. The particle can travel in any direction, but it resists axis orientation changes. I imagine, at periapsis, the spin axis orientation rate of change is greatest. One can see how spin axii are being tugged at all the time. But how does the spin orientation change anything?
So Miles has clarified my question. How can I transfer energy between the spin, and linear velocity?
Can it be just “resisting E/M field torque”?
Repeating
This paragraph sounds like explicit instructions that I’m too thick to see. Throw a curve ball.
.
Seveneves. Good old-fashioned, technically accurate, science fiction. Support your local library.Neal Stephenson wrote:Any curve you could make by slicing a cone with a plane-A circle, an ellipse, or a hyperbola-could be the shape of an orbit. For practical purposes, though, all orbits were ellipses. And most of the naturally occurring orbits in the solar system-those of the planets around the sun, or of moons around planets-were ellipses so round as to be indistinguishable, by the naked eye, from circles. This was not because nature especially favored circles. It was because highly elongated elliptical orbits tended not to last for very long. As a body in a highly eccentric orbit went rocketing in toward the central body and executed a hairpin turn at the periapsis-the point of closest approach-it was subject to tidal forces that could break it up.
Periapsis, that moment when the charge field’s relative influence is maximum. Normally, the spin axis acts gyroscopically. The particle can travel in any direction, but it resists axis orientation changes. I imagine, at periapsis, the spin axis orientation rate of change is greatest. One can see how spin axii are being tugged at all the time. But how does the spin orientation change anything?
174. The Third Wave: a Redefinition of Gravity, Part IV. Retrograde orbits, Triton, and the lack of angular momentum in the Sun are explained. 10pp. http://milesmathis.com/third4.htmlMiles wrote:Now let's return to my theory. There are two possibilities, neither of which is contradicted by data. I will offer the first one as the more likely. Let us say that the torque from Neptune works preferentially on the spin of Triton and not the velocity. In this case it would never appreciably affect the orbital momentum of Triton since Triton is so large. It might only affect the angular momentum, which decreases the energy of Triton's E/M field relative to Neptune's E/M field. In this way Triton loses energy but does not lose speed or radius. If this is the case, then we only have to look at the spin of Triton. Once the spin of Triton is stopped by Neptune, it must begin to reverse, since the torque from Neptune is constant. Eventually Triton will gain enough energy to create its own torque against the field of Neptune. At some point this torque will be sufficient to create a slight addition to orbital velocity, at which time Triton will bump itself into a higher orbit. The affect will become additive and eventually Triton will escape.
You may ask how a more energetic Triton turns that energy into orbital velocity. It does so with that resisting E/M field torque. That torque will have a component that is parallel to the orbit of Triton, and this must increase the orbital velocity. Even if we give the torque preferentially to the spin, there must be some point at which this preferential treatment breaks down. That is, once Triton gains some given amount of angular momentum, the torque can no longer be given to spin, preference or no. At that point the tangential component of the torque will begin affecting the velocity.
This would explain why major satellites do not impact their primaries. It would also explain why Triton's orbit decays so slowly.
The second possibility is a bit more revolutionary, but once again I believe it is capable of explaining more than current theory. Scientists know that Triton's retrograde orbit is decaying. They extrapolate from this to the assumption that it will eventually collide with Neptune. This, however, is a baseless assumption. It is true that Triton's orbit is decaying and that this decay is due to the fact that the orbit is losing energy. But there may be a limit to this decay. It is just possible that Triton's orbital velocity and spin will someday stop altogether, but that it will remain in orbit nonetheless, held at bay momentarily at its minimum orbital distance by the E/M field of Neptune. The field will keep applying a tangential torque to Triton—the same torque that made it lose energy—and it will begin gaining energy again. It will turn around and start orbiting in the opposite direction. It will move out into higher orbits until it reaches some kind of equilibrium with the E/M field of Neptune, at which time it will be a normal satellite in prograde, stable orbit.
So Miles has clarified my question. How can I transfer energy between the spin, and linear velocity?
Can it be just “resisting E/M field torque”?
Repeating
Miles wrote:That torque will have a component that is parallel to the orbit of Triton, and this must increase the orbital velocity. Even if we give the torque preferentially to the spin, there must be some point at which this preferential treatment breaks down. That is, once Triton gains some given amount of angular momentum, the torque can no longer be given to spin, preference or no. At that point the tangential component of the torque will begin affecting the velocity.
This paragraph sounds like explicit instructions that I’m too thick to see. Throw a curve ball.
.
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
 Re: Simple Orbiter 2
Re: Simple Orbiter 2
Open up my Proton Charge Viewer and think of the proton as the sun, or planet in this case, and the charge is, well, charge. Imagine a moon in between you and the central body and how the charge will affect that moon. It is the spin of the charge that is providing the tangential velocity.
Let's start with a few solidly placed vectors. The main vector is from the central body to the orbiting body. The tangential velocity vector of the moon is relative to the main vector. That is what it is tangential to. The charge of interest, that is, it hits our moon, is generally coming along the main vector, for simplicity. The sum of the spin components of that charge gives us a tangential force vector that we use to determine the applied force on the moon which can affect either its velocity or its spin. I would stick to velocity to start with.
Miles is saying that Triton has a velocity that opposes the tangential force vector, so it will lose energy. Eventually, it will reach zero and then, since that force is still there, it will start to gain energy in the direction of the tangential force vector.
This leads me to make some speculations:
The sum of spin on the charge photons can sum to zero. The tangential force vector would then be zero and provide no tangential velocity to any orbiting bodies. Our solar system has a 2:1 ratio of photons to anti-photons so it does not sum to zero. Are there solar systems that do not orbit but just sort of sit there as deep into the charge field of their star as possible? Would all of the planets cause each other to move based on their charge interactions?
If the tangential force is caused by an imbalance of charge to anti-charge, then the force is applied at either the top or the bottom of the orbiting body, not over its complete shell. This is not a nice clean push sideways. I think it would cause spin to a stationary orbiter. Therefore, the existing axial spin of the orbiter resists that spin and applies it as a torque to the whole body. That is, part of the force is used up working against the axial spin and the other part is allowed to express itself so the result is a sideways force.
The axial spin must be driven or it would soon stop. I think the axial spin is caused by the charge flowing through the orbiting body (north/south through-charge). Therefore the charge is working against itself (not the exact same photon but the mass of charge effecting the orbiter at a given time). This may result as heat and help explain the internal and external heat of planets.
The problem you face is how to calculate this stuff. It isn't easy and it's heavy with math. That's the joy and misery of programming, you have to fill in the gaps, you need all of the details. Focus on the vectors you have, what they represent and how they relate to the others. Then you might be able to see what you need to do with them to find the data you want. Draw them on a piece of paper, too, it really helps.
Let's start with a few solidly placed vectors. The main vector is from the central body to the orbiting body. The tangential velocity vector of the moon is relative to the main vector. That is what it is tangential to. The charge of interest, that is, it hits our moon, is generally coming along the main vector, for simplicity. The sum of the spin components of that charge gives us a tangential force vector that we use to determine the applied force on the moon which can affect either its velocity or its spin. I would stick to velocity to start with.
Miles is saying that Triton has a velocity that opposes the tangential force vector, so it will lose energy. Eventually, it will reach zero and then, since that force is still there, it will start to gain energy in the direction of the tangential force vector.
This leads me to make some speculations:
The sum of spin on the charge photons can sum to zero. The tangential force vector would then be zero and provide no tangential velocity to any orbiting bodies. Our solar system has a 2:1 ratio of photons to anti-photons so it does not sum to zero. Are there solar systems that do not orbit but just sort of sit there as deep into the charge field of their star as possible? Would all of the planets cause each other to move based on their charge interactions?
If the tangential force is caused by an imbalance of charge to anti-charge, then the force is applied at either the top or the bottom of the orbiting body, not over its complete shell. This is not a nice clean push sideways. I think it would cause spin to a stationary orbiter. Therefore, the existing axial spin of the orbiter resists that spin and applies it as a torque to the whole body. That is, part of the force is used up working against the axial spin and the other part is allowed to express itself so the result is a sideways force.
The axial spin must be driven or it would soon stop. I think the axial spin is caused by the charge flowing through the orbiting body (north/south through-charge). Therefore the charge is working against itself (not the exact same photon but the mass of charge effecting the orbiter at a given time). This may result as heat and help explain the internal and external heat of planets.
The problem you face is how to calculate this stuff. It isn't easy and it's heavy with math. That's the joy and misery of programming, you have to fill in the gaps, you need all of the details. Focus on the vectors you have, what they represent and how they relate to the others. Then you might be able to see what you need to do with them to find the data you want. Draw them on a piece of paper, too, it really helps.
 Re: Simple Orbiter 2
Re: Simple Orbiter 2
Chalk up a benchmark for SO2. I’ve included a working menu, (copied from webgl_gpgpu_birdsbirds)! Just like a finished working program.

As I’ve mentioned earlier, I have a slow/stable vs fast/chaotic simulation, depending on the number of particles, and gravity. After logging several hours of observation, trying to balance the two, I found the following relationship:
// # gravity
// 2 4
// 3 2.67
// 4 2
// 8 1
// 16 0.5
// 32 0.25
// 64 0.125
// 128 0.0625
// 256 0.03125
#*gravity =8
The relationship seems clear. I cannot just double the number of particles and keep the individual g values the same - high velocities, explosive collapses and spinouts are the result. The behavior may not be entirely inappropriate. But it clearly doesn't make sense to add x expansion fields directly. Tell me I'm wrong since this slows things down and gives me the 256 limit. Eventually I will try to try to model physical expansion more directly. Plenty to do.
Nevyn, Thanks for your previous post. You shared several points that beg consideration and discussion. Let me get back to that when I include spin.
.

As I’ve mentioned earlier, I have a slow/stable vs fast/chaotic simulation, depending on the number of particles, and gravity. After logging several hours of observation, trying to balance the two, I found the following relationship:
// # gravity
// 2 4
// 3 2.67
// 4 2
// 8 1
// 16 0.5
// 32 0.25
// 64 0.125
// 128 0.0625
// 256 0.03125
#*gravity =8
The relationship seems clear. I cannot just double the number of particles and keep the individual g values the same - high velocities, explosive collapses and spinouts are the result. The behavior may not be entirely inappropriate. But it clearly doesn't make sense to add x expansion fields directly. Tell me I'm wrong since this slows things down and gives me the 256 limit. Eventually I will try to try to model physical expansion more directly. Plenty to do.
Nevyn, Thanks for your previous post. You shared several points that beg consideration and discussion. Let me get back to that when I include spin.
.
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
 Re: Simple Orbiter 2
Re: Simple Orbiter 2
Another milestone, of sorts. I completed a run through of “Interactive 3D Graphics”, a http://threejs.org/ featured, free class put together by Eric Haines and based on threejs. http://www.udacity.com/overview/Course/cs291/.
Easily the best web class I've ever taken. An avalanche of information and additional sources, and I was ready for it. I’ll go back through it all again slowly.
.
Easily the best web class I've ever taken. An avalanche of information and additional sources, and I was ready for it. I’ll go back through it all again slowly.
.
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
 Re: Simple Orbiter 2
Re: Simple Orbiter 2
////////Somewhere in the initialization loop////////
boid.spinAxis.normalize();
//Sprites
var material = new THREE.SpriteCanvasMaterial( {
color: Math.random() * 0x808080 + 0x808080, program: program } );
spot = spots[ i ] = new THREE.Sprite( material );
spot.position.set(boid.position);
spot.scale.x = spot.scale.y = 10;
scene.add( spot );
//Spheres – 16 is max
var sphereGeom = new THREE.SphereGeometry( 3, 8, 8 );
var darkMaterial = new THREE.MeshBasicMaterial( { color: 0x000080 } );
var darkMaterial2 = new THREE.MeshLambertMaterial( { color: 0x000080 } );
var darkMaterial3 = new THREE.MeshPhongMaterial( { color: 0x000080 } );
sphere = spheres[ i ] = new THREE.Mesh( sphereGeom, darkMaterial );
sphere.position.set(boid.position);
// scene.add( sphere );
//Original Birds. See separate Bird.js
bird = birds[ i ] = new THREE.Mesh( new Bird(), new THREE.MeshBasicMaterial
( { color:000000, side: THREE.DoubleSide } ) );
bird.phase = Math.floor( Math.random() * 62.83 );
// scene.add( bird );
///////////////////////
Playing with three.js. My thoughts are still spinning.
Replaced the flapping winged bird with a round sprite I called spot. A very small performance improvement:
256 birds – 19 FramesPerSecond. 128 birds – 50 FPS.
256 spots – 21 FPS. 128 spots – 59 FPS.
32 spheres – 31 FPS. 16 spheres – 60 FPS.
I keep going in new directions. There are too many to choose from. Have you seen https://www.shadertoy.com ? Wow.
boid.spinAxis.normalize();
//Sprites
var material = new THREE.SpriteCanvasMaterial( {
color: Math.random() * 0x808080 + 0x808080, program: program } );
spot = spots[ i ] = new THREE.Sprite( material );
spot.position.set(boid.position);
spot.scale.x = spot.scale.y = 10;
scene.add( spot );
//Spheres – 16 is max
var sphereGeom = new THREE.SphereGeometry( 3, 8, 8 );
var darkMaterial = new THREE.MeshBasicMaterial( { color: 0x000080 } );
var darkMaterial2 = new THREE.MeshLambertMaterial( { color: 0x000080 } );
var darkMaterial3 = new THREE.MeshPhongMaterial( { color: 0x000080 } );
sphere = spheres[ i ] = new THREE.Mesh( sphereGeom, darkMaterial );
sphere.position.set(boid.position);
// scene.add( sphere );
//Original Birds. See separate Bird.js
bird = birds[ i ] = new THREE.Mesh( new Bird(), new THREE.MeshBasicMaterial
( { color:000000, side: THREE.DoubleSide } ) );
bird.phase = Math.floor( Math.random() * 62.83 );
// scene.add( bird );
///////////////////////
Playing with three.js. My thoughts are still spinning.
Replaced the flapping winged bird with a round sprite I called spot. A very small performance improvement:
256 birds – 19 FramesPerSecond. 128 birds – 50 FPS.
256 spots – 21 FPS. 128 spots – 59 FPS.
32 spheres – 31 FPS. 16 spheres – 60 FPS.
I keep going in new directions. There are too many to choose from. Have you seen https://www.shadertoy.com ? Wow.
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
 Re: Simple Orbiter 2
Re: Simple Orbiter 2
Hi Cr6, It might look like I know what I’m doing, but believe me, nothing is easy. I added an orbital camera - One of those luxuries that are now necessities. With just three lines of code, three.js allows one to move the viewing direction and distance. Of course, it’s quickly obvious that a cloud of particles offers no frame of reference. After several hours I was pleased to have solved nested i,j,k loops to give me a box set of volumetric markers. Then I found grid helpers that made my efforts moot.
Last week I forgot to say that sprites make perfectly passable particles. I can clearly see a periapsis swing which was lost in all the flapping. The multicolors also allow one to visually track one or more particles rather easily. I can also display the multicolor sprites on any color background, with maybe just a single stealth boid or two.
This has been quite a learning opportunity. Between you and me, I’m more confident than ever.
.
Last week I forgot to say that sprites make perfectly passable particles. I can clearly see a periapsis swing which was lost in all the flapping. The multicolors also allow one to visually track one or more particles rather easily. I can also display the multicolor sprites on any color background, with maybe just a single stealth boid or two.
This has been quite a learning opportunity. Between you and me, I’m more confident than ever.
.
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
 Re: Simple Orbiter 2
Re: Simple Orbiter 2
Status update; nothing tangible, just a fair amount of consideration.
So SO2 qualifies as a physics engine. I understand that a good developer would design an engine based on the anticipated collisions. In examining the balance of charge and gravity, this sim will violate conservation of both linear and angular momentum, as each particle is a source of charge repulsion as well as a seat of gravity. Currently, over time, the sim shows a slight increase in overall linear momentum, but the sim is far from complete.
I see normal particles traversing the simulation’s 1000 unit width, height or depth in less than 10 seconds, or an average of 100 units/second. The framerate, 60 per second, is able to handle this case, recalculating unit position changes of about 1.67. Higher speeds will involve recalculating position location changes of 2 units or more per frame. Translations of that magnitude cannot reflect accurate collision locations, although, apparently, particles are traveling too slow to pass through each other without interaction.
Currently, the fastest particles are “abnormal”, about twice as fast as normal particles. I assume their high speed is due to the acceleration delivered by the charge field of a particle upon another particle that came closer than the sum of the two particle’s “effective” radii. The boundary is still notional. This energy gets added to the total linear momentum displayed. I suppose I should do the calcs. I cleaned up some abnormal production with the tan acceleration.
Collision detection. After scanning a dozen or two sources, the eye-opener for me turned out to be an excellent description of “Sweep - and - prune”, or SAP, collision detection schemes/structures; http://www.codercorner.com/SAP.pdf, by Pierre Terdiman. Very nice, that is, while it’s still fresh in short term memory. I’ll try to clear up some thoughts as I go along.
Continuous SAP monitoring is expeditious and saves time in the long run. I would hate to drop another power of particles – 128 to 64 – as a result of increased CPU demands due to a poor collision implementation.
I appreciate the beauty of SAP, working with sorted lists to identify broad-phase collision locations requiring closer attention. SO2 is a little different. All forces due to all particles will be recalculated for each particle in turn. I believe it’s called brute force. Currently, for any possible collision, SO2 routinely performs the true collision test – what is the distance between the two particles? Is it smaller than the sum of the two radii? Even if the two radii are bounding spheres expanded by high velocities (just a wild thought). Any particle closer than, say, 5, should automatically be subject to the full collision treatment.
next morning...
I guess the full collision treatment should use both the current and previous position data for both particles (or maybe more).
.
So SO2 qualifies as a physics engine. I understand that a good developer would design an engine based on the anticipated collisions. In examining the balance of charge and gravity, this sim will violate conservation of both linear and angular momentum, as each particle is a source of charge repulsion as well as a seat of gravity. Currently, over time, the sim shows a slight increase in overall linear momentum, but the sim is far from complete.
I see normal particles traversing the simulation’s 1000 unit width, height or depth in less than 10 seconds, or an average of 100 units/second. The framerate, 60 per second, is able to handle this case, recalculating unit position changes of about 1.67. Higher speeds will involve recalculating position location changes of 2 units or more per frame. Translations of that magnitude cannot reflect accurate collision locations, although, apparently, particles are traveling too slow to pass through each other without interaction.
Currently, the fastest particles are “abnormal”, about twice as fast as normal particles. I assume their high speed is due to the acceleration delivered by the charge field of a particle upon another particle that came closer than the sum of the two particle’s “effective” radii. The boundary is still notional. This energy gets added to the total linear momentum displayed. I suppose I should do the calcs. I cleaned up some abnormal production with the tan acceleration.
Collision detection. After scanning a dozen or two sources, the eye-opener for me turned out to be an excellent description of “Sweep - and - prune”, or SAP, collision detection schemes/structures; http://www.codercorner.com/SAP.pdf, by Pierre Terdiman. Very nice, that is, while it’s still fresh in short term memory. I’ll try to clear up some thoughts as I go along.
Continuous SAP monitoring is expeditious and saves time in the long run. I would hate to drop another power of particles – 128 to 64 – as a result of increased CPU demands due to a poor collision implementation.
I appreciate the beauty of SAP, working with sorted lists to identify broad-phase collision locations requiring closer attention. SO2 is a little different. All forces due to all particles will be recalculated for each particle in turn. I believe it’s called brute force. Currently, for any possible collision, SO2 routinely performs the true collision test – what is the distance between the two particles? Is it smaller than the sum of the two radii? Even if the two radii are bounding spheres expanded by high velocities (just a wild thought). Any particle closer than, say, 5, should automatically be subject to the full collision treatment.
next morning...
I guess the full collision treatment should use both the current and previous position data for both particles (or maybe more).
.
Last edited by LongtimeAirman on Sun Dec 13, 2015 12:59 am; edited 1 time in total (Reason for editing : correct broad-band to broad-phase)
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
 Re: Simple Orbiter 2
Re: Simple Orbiter 2
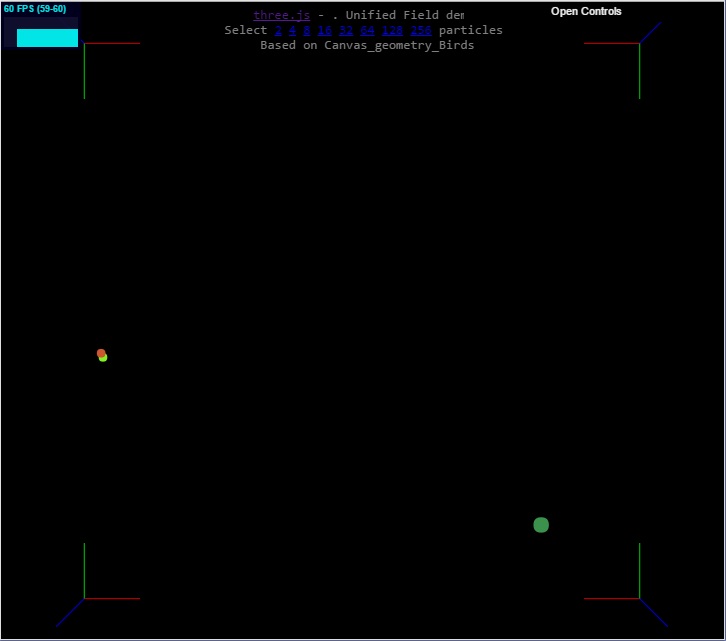
// HooAhhh, We have a collision at 9 o'clock.
////////////////////////////////////////////////////////////
this.gravAndChargeRepulsion = function ( boids ) {
var boid,
magAndDir = new THREE.Vector3(),
tanAcceleration = new THREE.Vector3(),
totalAcceleration = new THREE.Vector3();
totalAcceleration.set( 0, 0, 0 );
for ( var i = 0, il = boids.length; i < il; i ++ ) {
boid = boids[ i ];
// = boid.position.distanceTo( this.position );
distanceSquared = boid.position.distanceToSquared( this.position );
//grav = boid.gravity / boid.length;
if ( distanceSquared > 0.1) {
// changing from distance to distanceSquared didn't
// seem to effect the fps indications.
// grav = boid.gravity / distance;
// a. Gravity = 1/d, Expansion theory.;
grav = boid.gravity / distanceSquared;
// b. I've tried both. Maybe distSq is slower?
// Keep distanceSquared if only to avoid the very slow sqrt function.
magAndDir.subVectors(boid.position,this.position );
// magAndDir.normalize(); That was a mistake.
// Much better behaviour without it.
theta = boid.spinAxis.angleTo(magAndDir);
char = boid.charge * Math.sin( 2 * theta);
distance4 = (distanceSquared * distanceSquared);
char = char / distance4;
magAndDir.multiplyScalar(grav - char);
tanAcceleration.crossVectors( boid.spinAxis, magAndDir );
tanAcceleration.normalize();
tanAcceleration.multiplyScalar(char);
magAndDir.add(tanAcceleration);
totalAcceleration.add( magAndDir );
// Begin collision detection.
// Source, "Pool Hall Lessons: Fast, Accurate Collision
// Detection Between Circles or Spheres"
// http://www.gamasutra.com/view/feature/131424/pool_hall_lessons_fast_accurate_.php
// The single collision 3D dynamic reduces to a 2D known
// solution. In the reference, movevec is the moving circle
// velocity vector used to determine the collision contact
// point with a stationary circle.
// Here, movevec - the next this.velocity - won’t be
// calculated until totalAcceleration is known.
// For clarity: this.velocity resulted from adding
// the previous totalAcceleration to the previous
// this.velocity. The next this.velocity is created
// outside this i-loop and its host function
// this.gravAndChargeRepulsion(). Instead, movevec,
// or each new this.velocity, is created in the
// function this.move().
// The particle's current velocity, this.velocity, is a
// close approximation, good enough for escape tests.
// The particle pairs that fail the escape tests here
// will be collision candidates.
// I'll keep the source instructions, but change the
// names slightly so the differences with this
// implementation will be easier to follow.
// First my small addition, a benchmark test.
// create a reasonable closing frame separation distance
// threshold or things can slow down quickly. Current
// maximum particle speed appears to be about 3units/frame.
var VectorC = new THREE.Vector3();
// VectorC, the vector from the center of the moving circle
// A to the center of B. A length of 7.5 units amounts to more
// than twice the observed maximum velocity. The target is too
// far away and collision cannot occur within that frame.
VectorC.subVectors( boid.position, this.position );
if(VectorC.length ()> 7.5){
continue; }

// If the length of the approxMoveVec is less than the
// distance between the centers of these circles minus
// their radii, there's no way they can hit.
var approxMoveVec = new THREE.Vector3();
// approxMoveVec.addVectors(this.position,this.velocity);
approxMoveVec.addVectors(this.position,(this.velocity - boid.velocity));
// Note the two-moving sphere case.
var distSq;
var sumRadii = (this.radius + boid.radius);
var sumRadiiSquared = (this.radius + boid.radius) * (this.radius + boid.radius);
distSq = (VectorC.length * VectorC.length) - sumRadiiSquared;
if(approxMoveVec.lengthSq < (distSq)){
continue; }
var VectorN = new THREE.Vector3();
// Normalize the approxMoveVec
VectorN.copy(approxMoveVec);
VectorN.normalize();
// D = N . C = ||C|| * cos(angle between N and C)
var D = VectorN.dot(VectorC);
// Another early escape: Make sure that A is moving
// towards B! If the dot product between the
// approxMoveVec and B.center - A.center is less that
// or equal to 0, A isn't isn't moving towards B
if(D <= 0){
continue; }
var F = (VectorC.length * VectorC.length) - (D * D);
// Escape test: if the closest that A will get to B
// more than the sum of their radii, there's no
// way they are going collide
if(F >= sumRadiiSquared){
continue; }
// We now have F and sumRadii, two sides of a right triangle.
// Use these to find the third side, sqrt(T)
var T = sumRadiiSquared - F;
// If there is no such right triangle with sides length of
// sumRadii and sqrt(f), T will probably be less than 0.
// Better to check now than perform a square root of a
// negative number.
if(T < 0){
continue; }
// Therefore the distance the circle has to travel along
// approxMoveVec is D - sqrt(T)
var dist2;
dist2 = D - Math.sqrt(T);
// Get the magnitude of the movement vector
var mag = approxMoveVec.length();
// Finally, make sure that the distance A has to move
// to touch B is not greater than the magnitude of the
// movement vector.
if(mag < dist2){
continue; }
// And the final set of reference lines:
// Set the length of the movevec so that the circles will just touch.
// approxMoveVec.normalize();
// approxMoveVec.times(dist2);
// return true;
// OK, just me now. Going further is a waste of time
// without knowing the particle’s actual velocity.
system.out.println("dist2 is " + dist2);
// The system doesn't print anything, but the animation
// consistently freezes here with the collision visible.
// All I need to do is refresh to start it back up again.
// By the way, this is the most sophisticated stopping
// point test I've ever handled.
// So far, there's been no real penalty. With 256 particles,
// fps has held at 24, since adding the first test. Without it,
// 128 particles were clocking in at 29 fps.
// Still present at this point, we have this.position, aka
// boid = boids[ i ] from the function render(), and
// boid = boids[ i ] from this.gravAndChargeRepulsion()
// in a photo-finish.
// How would I pass them to this.moveCollisonBounceEtc
// or even to the return totalAcceleration level???
// Must every joy come with such pain?
}
}
return totalAcceleration;
};
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
 Re: Simple Orbiter 2
Re: Simple Orbiter 2
I admited being somewhat of a clod last week using the java cmd system.out.println as a programming tool. It reflected a certain desperation at the time. Then after a bout with an if-statement (testing equivalence - not making an assignment) I also realized that while I had studied Java, I had not yet studied JavaScript. So in my normal fashion, I went back to start, by beginning two new books: 1) http://eloquentjavascript.net/index.html; and 2) JavaScript: The Definitive guide. I loaded three.js Inspector but don’t see any utility to it yet. I also loaded Firebug on my Firefox. I am now using what I believe is a JavaScript console, to use the mini API cmd console.log(“doh”); to allow running javascript snippets or all the text examples on my browser. Also, an alert with variables listed has replaced system.out.println. Please forgive my loose use of the subject matter. Your patience is appreciated.
In any case, with less than a week left to this year, my best wishes to all for the next.
.
In any case, with less than a week left to this year, my best wishes to all for the next.
.
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
 Re: Simple Orbiter 2
Re: Simple Orbiter 2

Great Bouncing Me Tea Oids!
Allow me to repeat myself, Happy New Year!
Collisions and Bounces. Success. Even if I say so myself.
The collisions look OK. Most have the periapsis wiggle to some degree introduced by the charge field’s tanAcceleration. The wildest “collision” occurs when two boids roll around each other at high speed, a quirk or feature of SO2 caused when two bids are too close ( < 1. 0) to each other. It's hard to tell, but there's an example the image above, halfway up at 12 o'clock. I’ve seen them since last month, so, nothing special. Only now, they usually break free of each other, and are sometimes hit in collisions too. There are a few other wierdities, like occasional long range collisions.
Overall, stability is improved. The boids are now "tangible". The radii act as margins preventing the production of high accelerations. I tended to use radii between 1 and 10 in working the bounces. Size makes for poor differentiation in this simulation. I haven't tried a very large single central object yet. I have increased velocity, and gravity, because of the improved stability.
I apologise for the awful code I posted on the 18th. The reference source used thus far is the same as I identified then, but of course the errors were mine. My first test worked by hiding many errors, identifying collisions by fluke. Well, with effort (and //misery too!), I finally saw as the console.creator intended: Beginning with the revelation - a multitude of NaN's caused by vector.length; (answer. it needs() after length).
ToDoHere:
1)Create a separate collide function _collide(). Move citation. In this.gravAndChargeRepulsion,
a new _collide() would be used for collision detection; maybe it can be as simple as a flag or two. From this.move, _collide() would be the same as here, used to confirm collisions, and if true, calculate reactions. Presently, the Alerts below identify: a) the rare set (< the number of boids) of collide===true which occurred for me on two startups. b) Negative distances also occurred during view position changes. In my observation - after running many hours in the background, just a few sqSideT and sqSideF fails. As should be expected. They don't affect the simulation, it's just an observation. approxMoveVec and moveVec are almost the same. Easy enough to find out;
2) Find out;
3) Everything is still in debug over-expanded form; Too many variables.
4) All the errors still waiting. Like the occasional collision and one, two move, separated by many units, (50 or more).
4) Need collision sounds, great for monitoring the rate of collisions. And a counter(?).
5) This too is just a start. A vital and necessary one to move forward.
6) Spins. Will need to also transfer angular momentum.
///////////// this.move = function ()////////////////////
// Thanks to the overall, great n-particle engine, three.js canvas_geometry_birds
// found at http://threejs.org. Also thanks to the "Pool Hall Lessons: Fast, Accurate
// Collision Detection Between Circles or Spheres"
// http://www.gamasutra.com/view/feature/131424/pool_hall_lessons_fast_accurate_.php
this.move = function () {
if ( collide === true ) {
this.velocity.add( _acceleration );
boid = boids [counter];
// Use the true particle velocity, and the collision candidate
// boid. The other collision candidate is - this.(). D'oh meta!
var vectorC = new THREE.Vector3();
vectorC.subVectors(boid.position,this.position );
var distance = boid.position.distanceTo( this.position );
// distance - used during debug as a sanity check. With or
// without the alert("Working test distance = " + distance );
vecCSquared = vectorC.length() * vectorC.length();
var moveVec = new THREE.Vector3();
var diffVec = new THREE.Vector3();
// diffVec = ( boid.velocity - this.velocity );
// diffVec is the two-moving sphere case.
diffVec.copy(boid.velocity);
diffVec.sub(this.velocity);
moveVec.addVectors(this.position,diffVec);
// refQ: If the length of the moveVec is less than the
// refQ: distancebetween the centers of these circles
// refQ: minus their radii, there's no way they can hit.
var sumRadii = (this.radius + boid.radius);
var sumRadiiSquared = (this.radius + boid.radius) * (this.radius + boid.radius);
distSq = (vecCSquared) - sumRadiiSquared;
if( moveVec.lengthSq < distSq ){
_acceleration.set( 0, 0, 0 );
collide = false;
alert("Test 1 moveVec.lengthSq is less than distSq " + moveVec.lengthSq +" " + distSq );
};
var vectorN = new THREE.Vector3();
// Normalize the moveVec
vectorN.copy(moveVec);
vectorN.normalize();
//// sideD = vectorN . C = ||C|| * cos(angle between N and C)
var sideD = vectorN.dot(vectorC);
if(sideD <= 0){
_acceleration.set( 0, 0, 0 );
collide = false;
alert("Test 2. sideD < 0 " + sideD );
}
var sqSideF = (vectorC.length() * vectorC.length()) - (sideD * sideD);
if(sqSideF>=sumRadiiSquared){
_acceleration.set( 0, 0, 0 );
collide = false;
alert("Test 3. sqSideF >= sumRadiiSquared " + sqSideF +" " + sumRadiiSquared );
};
// refQ: If there is no such right triangle with sides length of
// refQ: sumRadii and sqrt(sqSideF), T sideT will probably be less than 0.
// refQ: Better to check now than perform a square root of a
// refQ: negative number.
var sqSideT = sumRadiiSquared - sqSideF;
if(sqSideT < 0){
_acceleration.set( 0, 0, 0 );
collide = false;
alert("Test 4. sqSideT < 0. sqSideT = " + sqSideT );
};
// refQ: Therefore the distance the circle has to travel along
// refQ: moveVec is sideD - sqrt(sqSideT)
var dist2Touch = sideD - Math.sqrt(sqSideT);
// refQ: Get the magnitude of the movement vector
var mag = moveVec.length();
// refQ: Finally, make sure that the distance A has to move
// refQ: to touch B is not greater than the magnitude of the
// refQ: movement vector.
if( mag < dist2Touch ){
_acceleration.set( 0, 0, 0 );
collide = false;
alert("Test 5. mag < dist2Touch" + mag +" " + dist2Touch );
};
// refQ: Set the length of the movevec so that the circles
// refQ: will just touch.
var moveVecToContact = new THREE.Vector3();
moveVecToContact.copy(moveVec);
// Keep the velocity vector intact
moveVecToContact.normalize();
moveVecToContact.multiplyScalar(dist2Touch);
var mag2 = moveVecToContact.length();
var frameBreak = mag2/mag;
// frameBreak is a number between 0 and 1. This
// represents the point in time (as a fraction
// of moveVec's possible extension as well as the
// current frame) the circles touched.
var thisHereVelocity = new THREE.Vector3();
thisHereVelocity.copy(this.velocity);
thisHereVelocity.multiplyScalar(frameBreak);
this.position.add(thisHereVelocity);
//this particle should be in position.
var copyBoidVelocity = new THREE.Vector3();
copyBoidVelocity.copy(boid.velocity);
copyBoidVelocity.multiplyScalar(frameBreak);
boid.position.add(copyBoidVelocity);
// boid should also be in position.
// Determine collision reaction. Still mainly
// as described in the source document.
// refQ: First, find the normalized vector n from the
// refQ: center of circle 1 to the center of circle2
var vectorCNC = new THREE.Vector3();
vectorCNC.copy(this.position);
vectorCNC.sub(boid.position);
vectorCNC.normalize();
// refQ: Find the length of the vectorCNC component
// refQ: of each of the movementvectors along n.
var a1 = this.velocity.dot(vectorCNC);
var a2 = boid.velocity.dot(vectorCNC);
// refQ: a2 = v2 . n
// refQ: float a1 = v1.dot(n);
// refQ: float a2 = v2.dot(n);
// refQ: Using the optimized version,
// refQ: optimizedP = 2(a1 - a2)
// refQ: -----------
// refQ: m1 + m2
// refQ: float optimizedP = (2.0 * (a1 - a2)) / (circle1.mass +
// refQ: circle2.mass);
var optimizedP;
optimizedP = (2.0 * (a1 - a2))/(this.mass + boid.mass);
// refQ: Calculate v1', the new movement vector of circle1
// refQ: v1' = v1 - optimizedP * m2 * n
// refQ: vectorNewV = this.velocity - optimizedP * circle2.mass * n;
var vectorV1Bounce = new THREE.Vector3();
vectorV1Bounce.copy(vectorCNC);
vectorV1Bounce.multiplyScalar(optimizedP*boid.mass);
var newThisVelocity = new THREE.Vector3();
newThisVelocity.copy(this.velocity);
newThisVelocity.sub(vectorV1Bounce);
this.velocity.copy(newThisVelocity);
newThisVelocity.multiplyScalar(1-frameBreak);
this.position.add(newThisVelocity);
var vectorV2Bounce = new THREE.Vector3();
vectorV2Bounce.copy(vectorCNC);
vectorV2Bounce.multiplyScalar(optimizedP*this.mass);
var newThisVelocity2 = new THREE.Vector3();
newThisVelocity2.copy(boid.velocity);
newThisVelocity2.add(vectorV2Bounce);
boid.velocity.copy(newThisVelocity2);
// boid.velocity.multiplyScalar(1-frameBreak);
// boid.position.add(boid.velocity);
// boid.velocity.multiplyScalar(1/(1-frameBreak));
// boid is advanced to contact, but not further,
// testing air-gap rebounds
_acceleration.set( 0, 0, 0 );
collide = false;
counter = -1;
}
else {
this.velocity.add( _acceleration );
this.position.add( this.velocity );
_acceleration.set( 0, 0, 0 );
};
if ( this.position.y > _height ) this.position.y = - _height;
if ( this.position.y < - _height ) this.position.y = _height;
if ( this.position.z > _depth ) this.position.z = - _depth;
if ( this.position.z < - _depth ) this.position.z = _depth;
// Don't ask
};
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
 Re: Simple Orbiter 2
Re: Simple Orbiter 2

I’m still working the collision stuff. Like eliminating penetrations. As you can see, I’m close to mastering the line-slope-intercept! Yes, implementing perfectly elastic 3d spherical collisions has been fairly straightforward:
1) Find the collision point, (use interpolation);
2) Move the two spheres along their velocity vectors to just "touch";
3) Find the contact plane and the normal between the two spheres;
4) Exchange linear momentum. Velocities parallel to the contact plane are unaffected, while velocities perpendicular to the plane are basically exchanged;
5) Move boids along their new velocities to their post collision positions.
The missing step - Exchange angular momentum.
Up to now, I've stuck to vectors. Points, positions, velocities, and accelerations are all vectors, although (of course) not all vectors are mathematically equal. (Miles has extensively described many of mainstream’s misuse of vectors). Angular momentum is directly analogous to linear momentum, with angular: mass, inertia, velocity and acceleration. The two momentums are entirely separate – though I’m on the record looking for where they can interact, beside any off-center collision. Solving the rotational system involves additional complexity, like following the correct ‘order of rotations’. Suffice to say, all the math used to exchange angular momentum that I’ve come across thus far is exceedingly difficult. If I knew what I was doing, I would say, “buck up, start enjoying matrix algebra”.
Please, there’s got to be a simpler way.
Both linear and angular momenta transfer forces through a contact point. Well, actually the contact area. Infinitesimal points do not exist and real objects deform; and friction... I’ll try again.
Observe the expected contact areas of two spheres just before they collide. I’ll list what I think are the few cases:
1.a. No spins. Head-on collision. Both contact areas approach each other without changing their angular position. The contact areas just clap together at the difference velocity of both spheres (like velocities of 1 and -1 meet with a difference velocity of 2). While all linear momenta may be transferred, there is no angular momenta present.
1.b. No spins. Off-center collision. The contact areas of the two spheres come together with equal and opposite translational surface velocities parallel to and not greater than the difference velocity of both spheres. Again there is no angular momenta (? I don't believe this. I 'll doublecheck, since off-center hits cause angular rotations).
2.a. Spins. Head-on collision. Both contact areas approach each other without changing their relative angular position. The contact areas just clap together. This is only possible if the contact area includes a pair of equal and opposite spin-axis anti-poles. Note that the rotational velocity is independent of the spheres’ forward velocity.
2.b. Spins. Head-on collision. When the same spin-axis poles come together, the contact areas come together with a contact plane rotation equal to the combined rotations of both spheres.
2.c. All other collisions between spinning spheres involve both the addition of parallel, forward translational parallel velocities; and another spin based surface velocity set that also varies velocities from zero to two. A zero differential surface velocity can occur during a glancing surface collision – actually more like a gentle rolling contact between two side-by-side anti-parallel spin-axis spheres on a plane containing both equators. The maximum velocity differential occurs between two side-by-side parallel spin-axis, the translational velocity in that opposite extreme case can reach four. A large variation.
The point I’m trying to make is that each surface point has a unique set of surface velocity variations that can define any sphere moving and spinning through space. I believe those additional vectors will allow a complete vector solution to collisions involving both linear and angular momenta.
Wishful thinking?
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
 Re: Simple Orbiter 2
Re: Simple Orbiter 2
Spin collisions are very difficult. I've reached the point you are at now and thought about the next step of introducing spin but haven't actually done it. I didn't need it for that particular project but have always had the idea of building a spin collision framework.
My suggestion is to keep it simple and add one thing at a time. Never work in angular units, always tangential velocities. Ignore inner spins, if you are heading towards stacked spins, until you need them (and you may not). A collision happens at a point, evaluate your spin values from that perspective. That point is the start of any velocity vectors you use whether they be linear or angular.
Your going to get into calculating angles between vectors and using some trig to figure out the resultant vector given 2 rotations. Compare the rotation axes of the particles: are they parallel or orthogonal or somewhere in between? Given the plane that the 2 axes are in, are they at equal levels (hitting at the equator of each particle) or are they at differing levels (hitting more at the top/bottom of the particles). These things effect how the collision happens.
You've posted some good diagrams already, keep working with those and just try to see the motions you are trying to work with. Look for any vectors or lines you can use to figure out things.
Good luck.
My suggestion is to keep it simple and add one thing at a time. Never work in angular units, always tangential velocities. Ignore inner spins, if you are heading towards stacked spins, until you need them (and you may not). A collision happens at a point, evaluate your spin values from that perspective. That point is the start of any velocity vectors you use whether they be linear or angular.
Your going to get into calculating angles between vectors and using some trig to figure out the resultant vector given 2 rotations. Compare the rotation axes of the particles: are they parallel or orthogonal or somewhere in between? Given the plane that the 2 axes are in, are they at equal levels (hitting at the equator of each particle) or are they at differing levels (hitting more at the top/bottom of the particles). These things effect how the collision happens.
You've posted some good diagrams already, keep working with those and just try to see the motions you are trying to work with. Look for any vectors or lines you can use to figure out things.
Good luck.
 Re: Simple Orbiter 2
Re: Simple Orbiter 2
Nevyn,
Thanks for the sanity check, and especially the constraint (no radians)!
In order to find actual collision points, I’m afraid one would need initial conditions and an axis rotation function – what I believe you recommended I avoid – and I agree.
I do have the boid object properties spin axis and rotation velocity (well, no rotVel yet actually, (say v=x at r=1)). We can estimate the spin tangential velocities through the relation, velAtLatitude = velAtEquator(cos(latitude)).

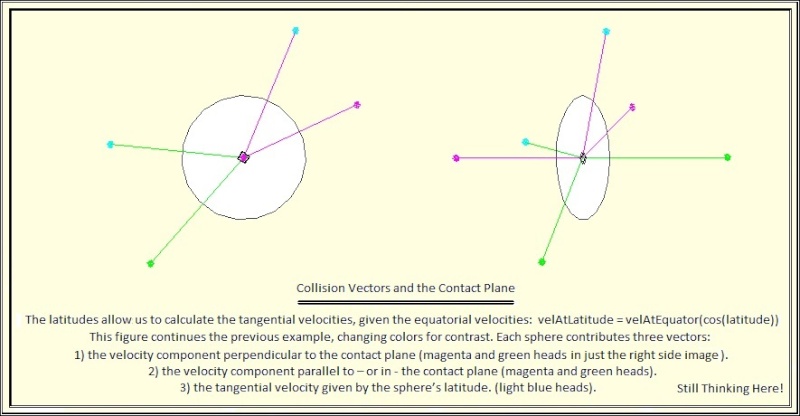
All vectors will be known, what better start?
.
Thanks for the sanity check, and especially the constraint (no radians)!
In order to find actual collision points, I’m afraid one would need initial conditions and an axis rotation function – what I believe you recommended I avoid – and I agree.
I do have the boid object properties spin axis and rotation velocity (well, no rotVel yet actually, (say v=x at r=1)). We can estimate the spin tangential velocities through the relation, velAtLatitude = velAtEquator(cos(latitude)).


All vectors will be known, what better start?
.
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
 Re: Simple Orbiter 2
Re: Simple Orbiter 2
I think you have misunderstood my statement. You can't avoid radians (and don't want to). All I meant is to avoid angular velocity values and stick to tangential velocity values. Keep everything straight as a good vector should be. Radians often give you horrible numbers but you can avoid that sometimes by working in units of PI. PI=180 degrees, PI/2=90, PI/4=45, etc, is much better than seeing 3.14, 1.57 or 0.707 although you will get used to reading radians if you keep at it long enough.
In your earlier posts, you had a picture of 2 spheres that were touching. The line between their centers is your baseline. Think of that line as being flat (along the X axis, say, but all I mean is that you consider the points to be the same in 2 dimensions and differ in the other). The collision point (assuming spheres of the same size, else divide accordingly) is half way along that line. Think of the collision point as being 0, 0, 0 and the baseline extends to either side of it in some dimension (X, say). Effectively, we have just created a translated and rotated coordinate system. This is just to think about, you won't need to create it in the math, it just helps to talk about the math by moving things to nice round numbers.
Now you need to figure out the direction of the spin axis of each particle with respect to the baseline. Find the angle between the baseline and the spin axis (the dot product, I think). If they are both perpendicular, ie 90deg, then you have an equator to equator collision. If an angle is less than 90 deg, then you are colliding near the top of that particle (but double check what a +ve rotation is in your 3D API as a <90 (actually it would be in radians, not degrees) value may mean you are colliding near the bottom rather than the top, I find it extremely helpful to create the points in the 3D scene so that you can see them and make sure they are where you expect).
Knowing the angle of attack allows you to calculate the tangential velocity from the collision point which allows you to determine the resultant velocity vectors. In the first instance, I would be tempted to just apply the resultant linear velocity vector to the existing linear velocity vectors and apply the resultant spin vector to the existing spin vectors. This will not lead to stacked spins but that is quite complicated and we don't really know how they work at this level. But it will allow you to fine tune the math and make sure you have that close to correct before complicating things.
That should get you thinking along the right lines. I haven't implemented anything this far along, but have thought about it a few times. Reading this thread makes me want to get back into the GPU code I wrote along these lines and extend it into a spin collision system.
In your earlier posts, you had a picture of 2 spheres that were touching. The line between their centers is your baseline. Think of that line as being flat (along the X axis, say, but all I mean is that you consider the points to be the same in 2 dimensions and differ in the other). The collision point (assuming spheres of the same size, else divide accordingly) is half way along that line. Think of the collision point as being 0, 0, 0 and the baseline extends to either side of it in some dimension (X, say). Effectively, we have just created a translated and rotated coordinate system. This is just to think about, you won't need to create it in the math, it just helps to talk about the math by moving things to nice round numbers.
Now you need to figure out the direction of the spin axis of each particle with respect to the baseline. Find the angle between the baseline and the spin axis (the dot product, I think). If they are both perpendicular, ie 90deg, then you have an equator to equator collision. If an angle is less than 90 deg, then you are colliding near the top of that particle (but double check what a +ve rotation is in your 3D API as a <90 (actually it would be in radians, not degrees) value may mean you are colliding near the bottom rather than the top, I find it extremely helpful to create the points in the 3D scene so that you can see them and make sure they are where you expect).
Knowing the angle of attack allows you to calculate the tangential velocity from the collision point which allows you to determine the resultant velocity vectors. In the first instance, I would be tempted to just apply the resultant linear velocity vector to the existing linear velocity vectors and apply the resultant spin vector to the existing spin vectors. This will not lead to stacked spins but that is quite complicated and we don't really know how they work at this level. But it will allow you to fine tune the math and make sure you have that close to correct before complicating things.
That should get you thinking along the right lines. I haven't implemented anything this far along, but have thought about it a few times. Reading this thread makes me want to get back into the GPU code I wrote along these lines and extend it into a spin collision system.
 Re: Simple Orbiter 2
Re: Simple Orbiter 2
Copy. Sanity check negative; time order reversal too. It is fun (and miserable)! Treading carefully...
Before simulating convincing spin collisions, or laying claim to a charge field demo, one must see spinning!
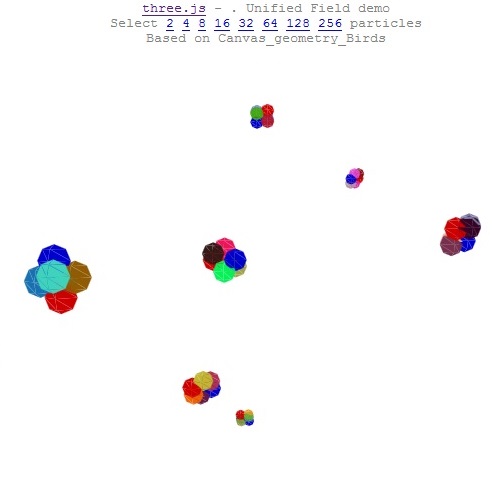
This image shows seven boi”particles”ds (previously manifest as single spheres, spots, and flapping birds), each comprised of 6 spheres. All the individual particles have the same radius; larger means closer to the viewer. Each of the seven clusters contains a red and blue pair of spheres - the north/south spin axis, randomly generated. The other 4 colors are also random, and positioned at +/- : eWAxis and fBAxis. These two axii are duplicates and rotations of spinAxis around its z and x axii, not true orthogonal rotations. That results in the small mix of shapes shown. Just a little interest. Again, I want to see spinning.
As yet, there is none. Each particle orientation is fixed as it travels and bounces about.
Where are those wires?
.
Before simulating convincing spin collisions, or laying claim to a charge field demo, one must see spinning!

This image shows seven boi”particles”ds (previously manifest as single spheres, spots, and flapping birds), each comprised of 6 spheres. All the individual particles have the same radius; larger means closer to the viewer. Each of the seven clusters contains a red and blue pair of spheres - the north/south spin axis, randomly generated. The other 4 colors are also random, and positioned at +/- : eWAxis and fBAxis. These two axii are duplicates and rotations of spinAxis around its z and x axii, not true orthogonal rotations. That results in the small mix of shapes shown. Just a little interest. Again, I want to see spinning.
As yet, there is none. Each particle orientation is fixed as it travels and bounces about.
Where are those wires?
.
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
 Re: Simple Orbiter 2
Re: Simple Orbiter 2

Yes, they spin.
I’m happy to say that tribute to Miles and the rest of you now includes a fine set of marbles, built from circles, spheres and sprites. Several images are superimposed above, involving many hours of object/parent/child lessons; clearly the child in me won – BIG!
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
 Re: Simple Orbiter 2
Re: Simple Orbiter 2
Thanks Cr6, I think they work like majic. Each is clearly visible, and when they're swarming they're every-which-way pretty. Of course their appearance doesn't make any difference in their behavior, but I'm not sure. The ortho shape is present in three of the four marbles, and it makes perfect sense. Each makes distinct visual spinwaves. Two spinrolling marbles make a case for spin stacking. I can easily see replacing them with all sorts of micro or macro objects.
Here's the init loop script. It seems more like a collection of ideas at present. I'm way behind. This last week was trying to restructure this.move. The joy was in having backup copies.
Thanks Nevyn, These models do have a way of multiplying one's understanding.
- Code:
<script>
var SCREEN_WIDTH = window.innerWidth,
SCREEN_HEIGHT = window.innerHeight,
SCREEN_WIDTH_HALF = SCREEN_WIDTH / 2,
SCREEN_HEIGHT_HALF = SCREEN_HEIGHT / 2;
var camera, scene, renderer;
var marble1, marble1s;
var marble2, marble2s;
var marble3, marble3s;
var marble4, marble4s;
var boid, boids, sphere, spheres, spot, spots;
var nSphere, nSpheres, sSphere, sSpheres;
var eSphere, eSpheres, wSphere, wSpheres;
var fSphere, fSpheres, bSphere, bSpheres;
var nSSphere, nSSpheres, eWSphere, eWSpheres;
var fBSphere, fBSpheres;
var boxEdges;
var stats;
//if ( ! Detector.webgl ) Detector.addGetWebGLMessage();
var hash = document.location.hash.substr( 1 );
if (hash) hash = parseInt(hash, 0);
// TEXTURE WIDTH FOR SIMULATION tied to the menu //
var WIDTH = hash || 16;
var BYRDS = WIDTH;
var PARTICLES = WIDTH;//Presents the current number of boids - Firefox doesn't show it.;
var BOUNDS = 800, BOUNDS_HALF = BOUNDS / 2;
//document.getElementById('boids').innerText = PARTICLES;
function change(n) {
location.hash = n;
location.reload();
return false;
}
var options = '';
for (i=1; i<9; i++) {
var j = Math.pow(2, i);
options += '<a href="#" onclick="return change(' + j + ')">' + (j) + '</a> ';
}
document.getElementById('options').innerHTML = options;
init();
animate();
function init() {
camera = new THREE.PerspectiveCamera( 55, SCREEN_WIDTH / SCREEN_HEIGHT, 1, 10000 );
camera.position.z = 600;
//Trying to add sound
//var listener = new THREE.AudioListener();
//camera.add( listener );
controls = new THREE.OrbitControls( camera );
controls.damping = 0.2;
controls.addEventListener( 'change', render );
scene = new THREE.Scene();
//scene.fog = new THREE.FogExp2( 0x9999ff, 0.00025 );//First try
//couldn't see it
// LIGHT
var light = new THREE.PointLight(0xffffff);
var ambientLight = new THREE.AmbientLight( 0x222222 );
light.position.set(100,250,100);
scene.add(light);
scene.add(ambientLight);
marble1s = [];
marble2s = [];
marble3s = [];
marble4s = [];
boids = [];
spheres = [];
nSpheres = [];
sSpheres = [];
eSpheres = [];
wSpheres = [];
fSpheres = [];
bSpheres = [];
nSSpheres = [];
eWSpheres = [];
fBSpheres = [];
spots = [];
//Show SpaceMarkers //////////////////////////////
var boxHW = 500;
var boxHH = 500;
var boxHD = 500;
var cLine = 100;
var lineMaterialR = new THREE.LineBasicMaterial( { color: 0xcc0000 , linewidth: 1.5 } );
var lineMaterialG = new THREE.LineBasicMaterial( { color: 0x00cc00 , linewidth: 1.5 } );
var lineMaterialB = new THREE.LineBasicMaterial( { color: 0x0000cc , linewidth: 1.5 } );
for ( var i = -1 ; i < 2; i = i + 2 ) {
for ( var j = -1 ; j < 2; j = j + 2 ) {
for ( var k = -1 ; k < 2; k = k + 2 ) {
var originX = new THREE.Geometry();
originX.vertices.push(
new THREE.Vector3((i * boxHW), (j * boxHH), (k * boxHD)),
new THREE.Vector3((i * (boxHW - cLine)), (j * boxHH), (k * boxHD)));
var originXLeg = new THREE.Line( originX, lineMaterialR );
scene.add(originXLeg);
var originY = new THREE.Geometry();
originY.vertices.push(
new THREE.Vector3((i * boxHW), (j * boxHH), (k * boxHD)),
new THREE.Vector3((i * boxHW), (j * (boxHH - cLine)), (k * boxHD)));
var originYLeg = new THREE.Line( originY, lineMaterialG );
scene.add(originYLeg);
var originZ = new THREE.Geometry();
originZ.vertices.push(
new THREE.Vector3((i * boxHW), (j * boxHH), (k * boxHD)),
new THREE.Vector3((i * boxHW), (j * boxHH), (k * (boxHD - cLine ))));
var originZLeg = new THREE.Line( originZ, lineMaterialB );
scene.add(originZLeg);
}
}
}
///////////Grid Helpers//////////////
var gridXZ = new THREE.GridHelper(boxHH, 100);
gridXZ.setColors( new THREE.Color(0x006600), new THREE.Color(0x006600) );
gridXZ.position.set( 0,-boxHH,0 );
//scene.add(gridXZ);
var gridXZ2 = new THREE.GridHelper(boxHH, 100);
gridXZ2.setColors( new THREE.Color(0x006600), new THREE.Color(0x006600) );
gridXZ2.position.set( 0,boxHH,0 );
//scene.add(gridXZ2);
var gridXY = new THREE.GridHelper(boxHD, 100);
gridXY.position.set( 0,0, -boxHD );
gridXY.rotation.x = Math.PI/2;
gridXY.setColors( new THREE.Color(0x000066), new THREE.Color(0x000066) );
//scene.add(gridXY);
var gridXY2 = new THREE.GridHelper(boxHD, 100);
gridXY2.position.set( 0,0, boxHD );
gridXY2.rotation.x = Math.PI/2;
gridXY2.setColors( new THREE.Color(0x000066), new THREE.Color(0x000066) );
//scene.add(gridXY2);
var gridYZ = new THREE.GridHelper(boxHW, 100);
gridYZ.position.set( boxHW, 0, 0 );
gridYZ.rotation.z = Math.PI/2;
gridYZ.setColors( new THREE.Color(0x660000), new THREE.Color(0x660000) );
//scene.add(gridYZ);
var gridYZ2 = new THREE.GridHelper(boxHW, 100);
gridYZ2.position.set( -boxHW, 0, 0 );
gridYZ2.rotation.z = Math.PI/2;
gridYZ2.setColors( new THREE.Color(0x660000), new THREE.Color(0x660000) );
//scene.add(gridYZ2);
/////////////////////////
for ( var i = 0; i < BYRDS; i ++ ) {
boid = boids[ i ] = new Boid();
//boid.position.x = (i*3)-300;
//boid.position.y = (i*2.5)-250;
//boid.position.z = (i*1.5)-150;
//boid.position.x = 0;
//boid.position.y = 0;
//boid.position.z = 0;
boid.position.x = Math.random() * 750 - 375;
boid.position.y = Math.random() * 750 - 375;
boid.position.z = Math.random() * 750 - 370;
boid.velocity.x = (Math.random()-0.5)*2;
boid.velocity.y = (Math.random()-0.5)*2;
boid.velocity.z = (Math.random()-0.5)*2;
boid.setAvoidWalls( true );
//Don't need walls. Will default to wraparound;
boid.setWorldSize( 800, 400, 400 );
boid.mass = 1;
boid.radius = 5;
boid.charge = 1;
//boid.gravity = 2;
boid.gravity = 8/BYRDS;
// boid.gravity should be adjusted as the # of boids varies.;
// Current thinking: For boid.length x, then boid.gravity =:
// x gravity ;
// 2 4 ;
// 3 2.67 ;
// 4 2 ;
// 8 1 ;
// 16 0.5 ;
// 32 0.25 ;
// 64 0.125 ;
// 128 0.0625 ;
// 256 0.03125 ;
// gravity = 8/x ;
// Doubling g from these values (ie. x*g=16)results in high velocities,;
// explosive collapses and spinouts. Unstable? But it ;
// doesn't make sense to me to add x expansion fields directly.;
// This x*gravity=8 seems real after several hours of observation.;
//spinning objects.
boid.spinAxis = new THREE.Vector3();
boid.spinAxis.x = Math.random() * 2 - 1;
boid.spinAxis.y = 1;
boid.spinAxis.z = Math.random() * 2 - 1;
boid.spinAxis.normalize();
//making a sprite
var PI2 = Math.PI * 2;
var program = function ( context ) {
context.beginPath();
context.arc( 0, 0, 0.5, 0, PI2, true );
context.fill();
}
//Sprites
var material = new THREE.SpriteCanvasMaterial( {
color: Math.random() * 0xfafbfc, program: program } );
spot = spots[ i ] = new THREE.Sprite( material );
spot.position.set(boid.position);
spot.scale.x = spot.scale.y = (boid.radius * 2.25);
scene.add( spot );
//Sphere parameters: radius, segments along width, segments along height
var sphereGeom = new THREE.SphereGeometry( boid.radius, 4, 4 );
//var darkMaterial = new THREE.MeshBasicMaterial( { color: 0xafafaf } );
var darkMaterial = new THREE.MeshBasicMaterial( { color: Math.random() * 0x808080 + 0x808080 } );
//var darkMaterialL = new THREE.MeshLambertMaterial( { color: 0x000080 } );
//var darkMaterialP = new THREE.MeshPhongMaterial( { color: 0x000080 } );
sphere = spheres[ i ] = new THREE.Mesh( sphereGeom, darkMaterial );
sphere.position.set(boid.position);
//scene.add( sphere );
/////////////////////////////////////////////////
//marbles
marble1 = marble1s[ i ] = new THREE.Object3D();
marble1.position.set( boids[ i ].position );
marble2 = marble2s[ i ] = new THREE.Object3D();
marble2.position.set( boids[ i ].position );
marble3 = marble3s[ i ] = new THREE.Object3D();
marble3.position.set( boids[ i ].position );
marble4 = marble4s[ i ] = new THREE.Object3D();
marble4.position.set( boids[ i ].position );
boid.spinPoles = new THREE.Vector3();
boid.spinPoles.copy(boid.spinAxis);
boid.spinPoles.multiplyScalar(boid.radius);
var poleGeom = new THREE.SphereGeometry( boid.radius/2, 3, 3 );
var nPoleMaterial = new THREE.MeshBasicMaterial( { color: 0xcc0000 } );
var sPoleMaterial = new THREE.MeshBasicMaterial( { color: 0x0000cc } );
var ePoleMaterial = new THREE.MeshBasicMaterial( { color: Math.random() * 0xfafbfc } );
var wPoleMaterial = new THREE.MeshBasicMaterial( { color: Math.random() * 0xfafbfc } );
var fPoleMaterial = new THREE.MeshBasicMaterial( { color: Math.random() * 0xfafbfc } );
var bPoleMaterial = new THREE.MeshBasicMaterial( { color: Math.random() * 0xfafbfc } );
nSphere = nSpheres[ i ] = new THREE.Mesh( poleGeom, nPoleMaterial );
sSphere = sSpheres[ i ] = new THREE.Mesh( poleGeom, sPoleMaterial );
eSphere = eSpheres[ i ] = new THREE.Mesh( poleGeom, ePoleMaterial );
wSphere = wSpheres[ i ] = new THREE.Mesh( poleGeom, wPoleMaterial );
fSphere = fSpheres[ i ] = new THREE.Mesh( poleGeom, fPoleMaterial );
bSphere = bSpheres[ i ] = new THREE.Mesh( poleGeom, bPoleMaterial );
var CircleGeometry = new THREE.CircleGeometry( boid.radius, 9 );
var nCircle = new THREE.Mesh( CircleGeometry, nPoleMaterial );
nCircle.rotation.x = -90 * Math.PI/180;
var sCircle = new THREE.Mesh( CircleGeometry, sPoleMaterial );
sCircle.rotation.x = 90 * Math.PI/180;
var eCircle = new THREE.Mesh( CircleGeometry, ePoleMaterial );
eCircle.rotation.y = 90 * Math.PI/180;
var wCircle = new THREE.Mesh( CircleGeometry, wPoleMaterial );
wCircle.rotation.y = -90 * Math.PI/180;
var fCircle = new THREE.Mesh( CircleGeometry, fPoleMaterial );
//fCircle.rotation.y = 0;
var bCircle = new THREE.Mesh( CircleGeometry, bPoleMaterial );
bCircle.rotation.x = 180 * Math.PI/180;
nSphere.position.y = boid.radius/2;
sSphere.position.y = -boid.radius/2;
eSphere.position.x = boid.radius/2;
wSphere.position.x = -boid.radius/2;
fSphere.position.z = boid.radius/2;
bSphere.position.z = -boid.radius/2;
//var nCircle1.copy(nCircle);
marble1.add( nCircle );
marble1.add( sCircle );
marble1.add( eCircle );
marble1.add( wCircle );
marble1.add( fCircle );
marble1.add( bCircle );
//scene.add( marble1 );
marble2.add( nSphere );
marble2.add( sSphere );
marble2.add( eSphere );
marble2.add( wSphere );
marble2.add( fSphere );
marble2.add( bSphere );
//scene.add( marble2 );
var coreMaterial = new THREE.MeshBasicMaterial( { color: Math.random() * 0xfafbfc } );
var coreBackMaterial = new THREE.MeshBasicMaterial( { color: Math.random() * 0xfcfbfa } );
var CircleGeometry = new THREE.CircleGeometry( boid.radius, 9 );
for ( var j = 0; j < 3; j ++ ) {
var coreCircle = new THREE.Mesh( CircleGeometry, coreMaterial );
coreCircle.rotation.x = j * 120 * Math.PI/180;
marble3.add( coreCircle );
var coreBackCircle = new THREE.Mesh( CircleGeometry, coreBackMaterial );
coreBackCircle.rotation.x = j * 120 * Math.PI/180;
coreBackCircle.rotation.y = 180 * Math.PI/180;
marble3.add( coreBackCircle );
}
scene.add( marble3 );
//var nSSphereMaterial = new THREE.MeshBasicMaterial( { color: Math.random() * 0xfafbfc } );
//var eWSphereMaterial = new THREE.MeshBasicMaterial( { color: Math.random() * 0xfafbfc } );
//var fBSphereMaterial = new THREE.MeshBasicMaterial( { color: Math.random() * 0xfafbfc } );
//nSSphere = nSSpheres[ i ] = new THREE.Mesh(
// new THREE.SphereGeometry( boid.radius, 8, 8 ), nSSphereMaterial);
//nSSphere.scale.x = 0.1;
//nSSphere.scale.y = 1.0;
//nSSphere.scale.z = 0.1;
//nSSphere.rotation.y = 30* Math.PI/180;
//eWSphere = eWSpheres[ i ] = new THREE.Mesh(
// new THREE.SphereGeometry( boid.radius, 8, 8 ), eWSphereMaterial);
//eWSphere.scale.x = 1;
//eWSphere.scale.y = 0.1;
//eWSphere.scale.z = 0.1;
//fBSphere = fBSpheres[ i ] = new THREE.Mesh(
// new THREE.SphereGeometry( boid.radius, 8, 8 ), fBSphereMaterial);
//fBSphere.scale.x = 0.1;
//fBSphere.scale.y = 0.1;
//fBSphere.scale.z = 1;
//marble4.add( nSSphere );
//marble4.add( eWSphere );
//marble4.add( fBSphere );
//scene.add( marble4 );
// Will probably delete above. The pin axis will change over time even
// without collisions.. I guess it doesn't make sense to try to
// rotate the sphere this way. Spin axis changes will occur
//
//Sphere parameters: radius, segments along width, segments along height
var sphereCGeom = new THREE.SphereGeometry( boid.radius, 4, 4 );
//var darkMaterial = new THREE.MeshBasicMaterial( { color: 0xafafaf } );
var darkCMaterial = new THREE.MeshBasicMaterial( { color: Math.random() * 0x808080 + 0x808080 } );
//var darkMaterialL = new THREE.MeshLambertMaterial( { color: 0x000080 } );
//var darkMaterialP = new THREE.MeshPhongMaterial( { color: 0x000080 } );
nSSphere = nSSpheres[ i ];
nSSphere = new THREE.Mesh( sphereCGeom, darkCMaterial );
nSSphere.scale.x = 0.1;
nSSphere.scale.y = 1.0;
nSSphere.scale.z = 0.1;
eWSphere = eWSpheres[ i ];
eWSphere = new THREE.Mesh( sphereCGeom, darkCMaterial );
eWSphere.scale.x = 1;
eWSphere.scale.y = 0.1;
eWSphere.scale.z = 0.1;
fBSphere = eWSpheres[ i ];
fBSphere = new THREE.Mesh( sphereCGeom, darkCMaterial );
fBSphere.scale.x = 0.1;
fBSphere.scale.y = 0.1;
fBSphere.scale.z = 1;
marble4.add( nSSphere );
marble4.add( eWSphere );
marble4.add( fBSphere );
//scene.add( marble4 );
}
renderer = new THREE.CanvasRenderer();
//renderer.setClearColor( 0x000000 );
//renderer.setClearColor( 0x0000af );
renderer.setClearColor( 0xffffff );
renderer.setPixelRatio( window.devicePixelRatio );
renderer.setSize( SCREEN_WIDTH, SCREEN_HEIGHT );
//document.addEventListener( 'mousemove', onDocumentMouseMove, false );
document.body.appendChild( renderer.domElement );
stats = new Stats();
stats.domElement.style.position = 'absolute';
stats.domElement.style.left = '0px';
stats.domElement.style.top = '0px';
document.getElementById( 'container' ).appendChild(stats.domElement);
window.addEventListener( 'resize', onWindowResize, false );
//////////////////////////////////
var gui = new dat.GUI();
var parameters =
{
a: 200, // numeric
b: 200, // numeric slider
c: "Hello, GUI!", // string
d: false, // boolean (checkbox)
e: "#ff8800", // color (hex)
f: function() { alert("Stop!") },
g: function() { alert( parameters.c ) },
v : 0, // dummy value, only type is important
w: "...", // dummy value, only type is important
x: 0, y: 0, z: 0
};
/////////////////////////////////////////////////////
//gui.add( parameters )
gui.add( parameters, 'a' ).name('Number');
gui.add( parameters, 'b' ).min(128).max(256).step(16).name('Slider');
gui.add( parameters, 'c' ).name('String');
gui.add( parameters, 'd' ).name('Boolean');
gui.addColor( parameters, 'e' ).name('Color');
var numberList = [1, 2, 3];
gui.add( parameters, 'v', numberList ).name('List');
var stringList = ["One", "Two", "Three"];
gui.add( parameters, 'w', stringList ).name('List');
gui.add( parameters, 'f' ).name('Please "Stop!"');
gui.add( parameters, 'g' ).name("Alert Message");
var folder1 = gui.addFolder('Coordinates');
folder1.add( parameters, 'x' );
folder1.add( parameters, 'y' );
folder1.close();
gui.close();
}
/////////////////////////////////////////////////////
function onWindowResize() {
camera.aspect = window.innerWidth / window.innerHeight;
camera.updateProjectionMatrix();
renderer.setSize( window.innerWidth, window.innerHeight );
}
function animate() {
requestAnimationFrame( animate );
render();
stats.update();
}
function render() {
for ( var i = 0, il = boids.length; i < il; i++ ) {
boid = boids[ i ];
boid.run( boids );
spheres[ i ].position.copy( boids[ i ].position );
spot = spots[ i ];
spot.position.copy( boids[ i ].position );
marble1 = marble1s[i];
marble1.position.copy( boids[ i ].position );
marble1.rotateOnAxis (boid.spinAxis, 5 * Math.PI/180);
marble2 = marble2s[i];
marble2.position.copy( boids[ i ].position );
marble2.rotateOnAxis (boid.spinAxis, 5 * Math.PI/180);
marble3 = marble3s[i];
marble3.position.copy( boids[ i ].position );
marble3.rotateOnAxis (boid.spinAxis, 5 * Math.PI/180);
marble4 = marble4s[i];
marble4.position.copy( boids[ i ].position );
marble4.rotateOnAxis (boid.spinAxis, 5 * Math.PI/180);
}
renderer.render( scene, camera );
}
</script>
Here's the init loop script. It seems more like a collection of ideas at present. I'm way behind. This last week was trying to restructure this.move. The joy was in having backup copies.
Thanks Nevyn, These models do have a way of multiplying one's understanding.
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
 Re: Simple Orbiter 2
Re: Simple Orbiter 2
I’d like to call attention to a gem from The American Journal of Physics, vol. 37, no. 1, January 1969, Kinematics of an Ultraelastic Rough Ball. http://www.rpi.edu/dept/phys/courses/PHYS1150/GarwinSuperBall.pdf. The math is turning out to be a favorite - translational and angular momentum exchanges in collisions between a superball and stationary surfaces – well, maybe someday. The analysis is clear and leads to an Ultraelastic Rough collision matrix.
The paper’s biggest surprise, I think it’s fair to say, is oscillation between translational and angular velocities from one collision to the next. The first bounce converts translational velocity to angular velocity, which is converted back to translational velocity after the next bounce. In effect, superballs take extra - almost vertical - bounces to get to wherever they’re going - translationally, compared with ‘normal’ balls. I guess that accounts for the “Ultra” in the paper’s title. If I understand correctly, the difference isn’t due to ‘slip’, it’s due to asynchronous energy reaction periods relating to the mass density distribution within the sphere … ? I’ll keep it in mind.
OK, Pop Quiz.
Inspector Clouseau leans on a globe,
in which direction will he go?
The trick answer is - east. We all travel east as the world turns below us. The answer I’m looking for is east or west, as the globe, fixed on its N-S axis is free to turn only in the E-W ‘directions’. The globe’s resulting angular velocity is due to the tangential acceleration provided by Clouseau’s elbow.
When two spheres collide, the primary sources of angular momentum are the two collision latitude tangential velocities. I’ll assert that these two velocities are the primary directions, even though they don’t usually align and I don’t understand how they interact yet.
We also have the translational velocity vectors that are ignored in the linear energy exchange, since they are in the contact plane. These must be replaced with new projections parallel or perpendicular to the tangential velocities. They remain within the contact plane to add or subtract from the main tangential vectors.
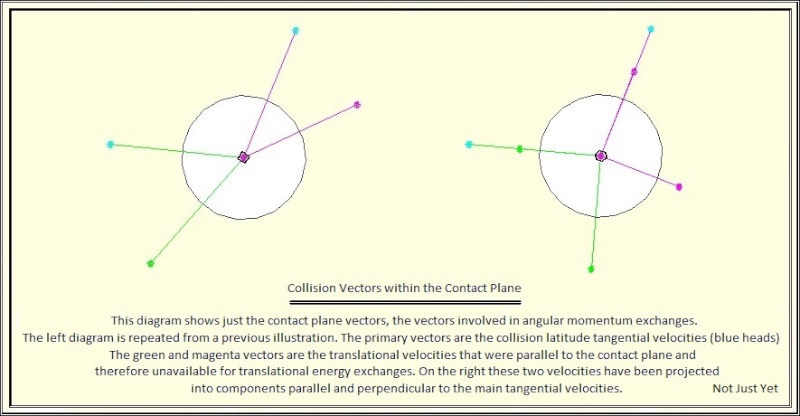
I think I'll begin by exchanging these velocity vectors within the existing spin axii. If there is not enough existing angular momenta to cover the exchange, then I guess the spin axis orientation should somehow make up the difference.
Note. I’m coming full circle. How does a sphere respond to the charge field? Does it get slowed down to the point where the spin axis begins to change? I see now how a charge differential front to back may speed-up or slow–down transverse tangential velocities. I can also see the same differential turning the spin axis. In my optimistic viewpoint, the charge field differential mechanism flows seamlessly to these collisions.
That's where I'm at.
The paper’s biggest surprise, I think it’s fair to say, is oscillation between translational and angular velocities from one collision to the next. The first bounce converts translational velocity to angular velocity, which is converted back to translational velocity after the next bounce. In effect, superballs take extra - almost vertical - bounces to get to wherever they’re going - translationally, compared with ‘normal’ balls. I guess that accounts for the “Ultra” in the paper’s title. If I understand correctly, the difference isn’t due to ‘slip’, it’s due to asynchronous energy reaction periods relating to the mass density distribution within the sphere … ? I’ll keep it in mind.
OK, Pop Quiz.
Inspector Clouseau leans on a globe,
in which direction will he go?
The trick answer is - east. We all travel east as the world turns below us. The answer I’m looking for is east or west, as the globe, fixed on its N-S axis is free to turn only in the E-W ‘directions’. The globe’s resulting angular velocity is due to the tangential acceleration provided by Clouseau’s elbow.
When two spheres collide, the primary sources of angular momentum are the two collision latitude tangential velocities. I’ll assert that these two velocities are the primary directions, even though they don’t usually align and I don’t understand how they interact yet.
We also have the translational velocity vectors that are ignored in the linear energy exchange, since they are in the contact plane. These must be replaced with new projections parallel or perpendicular to the tangential velocities. They remain within the contact plane to add or subtract from the main tangential vectors.

I think I'll begin by exchanging these velocity vectors within the existing spin axii. If there is not enough existing angular momenta to cover the exchange, then I guess the spin axis orientation should somehow make up the difference.
Note. I’m coming full circle. How does a sphere respond to the charge field? Does it get slowed down to the point where the spin axis begins to change? I see now how a charge differential front to back may speed-up or slow–down transverse tangential velocities. I can also see the same differential turning the spin axis. In my optimistic viewpoint, the charge field differential mechanism flows seamlessly to these collisions.
That's where I'm at.
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
 Re: Simple Orbiter 2
Re: Simple Orbiter 2

Quick update. I've started coding the Angular Momentum Exchange shown above. I have both sets of latVels and transVels.
Next, I'll project each sphere's set to the other. It's too soon to share the code.
Two additional examples are included for your consideration.

Last edited by LongtimeAirman on Fri Feb 19, 2016 7:40 pm; edited 1 time in total (Reason for editing : Correcting bottom right diagram)
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
 Re: Simple Orbiter 2
Re: Simple Orbiter 2
Very ambitious and cool to boot.
I just wanted to throw out these links if it helps any with the new library:
Four dimensional rational spherical coordinates (Chapter 27 of Divine Proportions)
http://web.maths.unsw.edu.au/~norman/papers/Chapter27.pdf
https://www.youtube.com/watch?v=Cc8qd7zB2Io
https://milesmathis.forumotion.com/t42-quaternions
I just wanted to throw out these links if it helps any with the new library:
Four dimensional rational spherical coordinates (Chapter 27 of Divine Proportions)
http://web.maths.unsw.edu.au/~norman/papers/Chapter27.pdf
https://www.youtube.com/watch?v=Cc8qd7zB2Io
https://milesmathis.forumotion.com/t42-quaternions
 Re: Simple Orbiter 2
Re: Simple Orbiter 2
Cr6, "Ambitious"? Maybe single-mindedness – must be a vector solution - "and cool to boot". Yes, SO2 is already a nice particle engine.
There are many ways to use or improve it. With just randomly placed spinning marbles and linear collisions it looks and works better than I'd hoped. Of course there are still plenty of bugs. Maybe I should clean it up as is and upload it to GitHub as thanks for Birds. I could also change it to pursue my own game ideas; believe it or not, my goal (25 years ago) was to program a 3D pool game, but for lack of a compiler (s/w) I changed my hobby to stained glass/metal sculpture instead.
I wouldn’t consider SO2 finished until Nevyn or you told me it was. On the practical side, I’ll see if the angular collisions are working or not. I also believe the continuum - charge differential to tangential velocity to collisions – should be elegant. And stacking spins, I’m nowhere near stacking spins yet, except maybe I am. How many discreet spins should a marble have anyway?
Thanks for reminding me that rational trigonometry should be part of the solution. While I declare that the latitudinal velocity is the mainline, what happens if the spin velocity is low, or the latitude is close to the spin Axis pole? At what ‘rate’ will the translational velocity become the mainline. Will conversion to quaternions enable me to directly add the two?
I jumped into the blue with a good deal of math trepidation and joy. Did you throw a jet pack at me? Are you working on Library ideas?
There are many ways to use or improve it. With just randomly placed spinning marbles and linear collisions it looks and works better than I'd hoped. Of course there are still plenty of bugs. Maybe I should clean it up as is and upload it to GitHub as thanks for Birds. I could also change it to pursue my own game ideas; believe it or not, my goal (25 years ago) was to program a 3D pool game, but for lack of a compiler (s/w) I changed my hobby to stained glass/metal sculpture instead.
I wouldn’t consider SO2 finished until Nevyn or you told me it was. On the practical side, I’ll see if the angular collisions are working or not. I also believe the continuum - charge differential to tangential velocity to collisions – should be elegant. And stacking spins, I’m nowhere near stacking spins yet, except maybe I am. How many discreet spins should a marble have anyway?
Thanks for reminding me that rational trigonometry should be part of the solution. While I declare that the latitudinal velocity is the mainline, what happens if the spin velocity is low, or the latitude is close to the spin Axis pole? At what ‘rate’ will the translational velocity become the mainline. Will conversion to quaternions enable me to directly add the two?
I jumped into the blue with a good deal of math trepidation and joy. Did you throw a jet pack at me? Are you working on Library ideas?
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
 Re: Simple Orbiter 2
Re: Simple Orbiter 2
LTAM, I just have always found Sine, Cosine, Tangent, etc. as "lookup book values" that maybe Rational Trig could give a more simplified approach in some cases? It would be a lot of work to make a new Javascript library that could imitate something like three.js with Rational Trig but down the road it might provide flexibility for matrix math (hits/direction/rotation/speed), etc. If I'm rambling, I blame the Whiskey.
https://en.wikipedia.org/wiki/Lookup_table#Computing_sines
https://upload.wikimedia.org/wikipedia/commons/thumb/3/3b/Circle_cos_sin.gif/450px-Circle_cos_sin.gif
This book has a few indications of classical "QT" electron matrix math with eigenvalues. The math is "waaayy tooo deeep" for my humble abilities.
C. Graaf and R. Broer,
Magnetic Interactions in Molecules and Solids
Theoretical Chemistry and Computational Modelling
Chapter 1:
1.2 Generation of Many Electron Spin Functions
1.2.1 Many Electron Spin Functions by Projection
----
Can't say that I've ever made a practical "kitchen sink" from these random ideas.
https://en.wikipedia.org/wiki/Lookup_table#Computing_sines
https://upload.wikimedia.org/wikipedia/commons/thumb/3/3b/Circle_cos_sin.gif/450px-Circle_cos_sin.gif
This book has a few indications of classical "QT" electron matrix math with eigenvalues. The math is "waaayy tooo deeep" for my humble abilities.
C. Graaf and R. Broer,
Magnetic Interactions in Molecules and Solids
Theoretical Chemistry and Computational Modelling
Chapter 1:
1.2 Generation of Many Electron Spin Functions
1.2.1 Many Electron Spin Functions by Projection
----
Can't say that I've ever made a practical "kitchen sink" from these random ideas.
Good questions, and is the program built for the viewer or just the objects without a viewer?While I declare that the latitudinal velocity is the mainline, what happens if the spin velocity is low, or the latitude is close to the spin Axis pole? At what ‘rate’ will the translational velocity become the mainline. Will conversion to quaternions enable me to directly add the two?
 Re: Simple Orbiter 2
Re: Simple Orbiter 2
Nevyn, I'm happy with the results of this project so far. I’ve presented bits and pieces of Simple Orbiter as evidence of progress, certain you or someone at home could reassemble them, and, with half a mind, do better.
Have you or Cr6 seen this thing? I’d hate it if some danged old newby died hogging a Charge Field simulation waiting for angular inspiration.
I’d like to post a first draft. Maybe organize it a bit. As you know, this project is far from finished. I intend to do as good a job as I’m able and turn it over to you. I’d appreciate any instructions you may have for me toward that end.
For the last month I’ve been in virtual orbit. I’m better prepared to share discussion and interpretations on the subject of the interaction of charged particles.
.
Have you or Cr6 seen this thing? I’d hate it if some danged old newby died hogging a Charge Field simulation waiting for angular inspiration.
I’d like to post a first draft. Maybe organize it a bit. As you know, this project is far from finished. I intend to do as good a job as I’m able and turn it over to you. I’d appreciate any instructions you may have for me toward that end.
For the last month I’ve been in virtual orbit. I’m better prepared to share discussion and interpretations on the subject of the interaction of charged particles.
.
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
 Re: Simple Orbiter 2
Re: Simple Orbiter 2
Cr6,
Nevyn PMed me to zip and send Simple Orbiter to him, so I did. I would have sent it to you but MM the Site won’t let me attach zip files. Worse, my mail server doesn’t have any messages from you. I word searched your name in my files and hit on compendium, but no further. I’ve been whiling away time going through your 15MB monster – how do you navigate through it? Lots of additional stuff, and I do love the pictures.
Send me a gmail message so I can send SO2 to you too. Then be amazed!
Nevyn PMed me to zip and send Simple Orbiter to him, so I did. I would have sent it to you but MM the Site won’t let me attach zip files. Worse, my mail server doesn’t have any messages from you. I word searched your name in my files and hit on compendium, but no further. I’ve been whiling away time going through your 15MB monster – how do you navigate through it? Lots of additional stuff, and I do love the pictures.
Send me a gmail message so I can send SO2 to you too. Then be amazed!
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
 Re: Simple Orbiter 2
Re: Simple Orbiter 2
LongtimeAirman wrote:Cr6,
Nevyn PMed me to zip and send Simple Orbiter to him, so I did. I would have sent it to you but MM the Site won’t let me attach zip files. Worse, my mail server doesn’t have any messages from you. I word searched your name in my files and hit on compendium, but no further. I’ve been whiling away time going through your 15MB monster – how do you navigate through it? Lots of additional stuff, and I do love the pictures.
Send me a gmail message so I can send SO2 to you too. Then be amazed!
Okay LTAM,
Let me send you all my personal email in a PM. I don't know if I'll be much help with three.js issues. I'll have to defer to Neyvn's powers with that one.
I did look over mrdoob's github entries and noticed he makes fairly frequent updates. There's always a potential situation where you might stumble on to a bug in one of the libraries -- a lot of it looks taken from good 3-D C++ libraries built in the past. I should have looked at this closer before posting my prior post. Looks like three.js is using Quaternions/Slerp/etc. routines. I guess I better shut my mouth.
The only question is, do we have everything needed in three.js to represent Mathis' spin mechanics/collisions?
By the way, I'm fully cognizant of the time and effort it takes to "create" an original work programming this. Nevyn's work and your work here just simply impresses.
https://github.com/mrdoob/three.js/tree/master/src/math
 Re: Simple Orbiter 2
Re: Simple Orbiter 2
Cr6, Zip launched, message deleted (or not saved anyway).
Downloading mrdoob-three.js and viewing the examples is a necessary yet motivating experience.
We're friends here. A new first draft, feel free to break it.
Enjoy
.
Downloading mrdoob-three.js and viewing the examples is a necessary yet motivating experience.
We're friends here. A new first draft, feel free to break it.
Enjoy
.
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
 Re: Simple Orbiter 2
Re: Simple Orbiter 2
Cr6 wrote:
The only question is, do we have everything needed in three.js to represent Mathis' spin mechanics/collisions?
Yes, everything required is in ThreeJS. Most of it is just math and decisions based on the mechanics. ThreeJS allows us to visualize it and also provides some handy things like vectors, matrices, quaternions, etc to help with the calculations.
My main question at the moment is what kind of system I want to build. You can look at it from really close up where you are watching a limited number of particles collide to get that fine detail of the collisions and how spins are gained/lost. On the other hand, you can look at it from afar where you have lots of particles colliding and you want to look at the field rather than the particles.
I want both but I think, at the moment, we all need a closer look at spin mechanics in action to get a better understanding of the quantum world. So I am leaning towards the former but I feel that the latter will kind of fall out of it. Once I have that spin mechanics behavior, I can apply it to other systems and it should be relatively easier to create the field model once I have the collision model. The difference is more to do with performance than anything else.
 Re: Simple Orbiter 2
Re: Simple Orbiter 2
Update
The particles already show a surprising range of spin behavior, including a slingshot effect. Two or more particles can whip around each other in constant contact for several ‘orbits’ before disappearing in some wild acceleration. I’ve tried to slow it down, but this is first draft. I thought I could somehow mirror or extend the action to the collisions.
“I’ll Try This!” immediately resulted in very high equatorial velocities. Translational velocities are easily converted to spin, while I have no mechanism to shed spin except through collision. To paraphrase a colleague, spins are hard.
I took a break from Boids. A non-stop politics binge. I want to be sick.
So, back to subject. I’ll put a couple of thoughts out there.
Pretty as it is, Boids is still mostly charged points. The unexpected spin behavior is not real.
Starting where I'm at, I think I can model close particle interaction as pre-e/m strength changes along quadrature lines (30N/30S/30E/30W), radially expanding, where the time or charge density is also dependent on the equatorial velocity, etc.
That drives the total number of particles down but I’d rather see a few as accurately as possible at this point.
The particles already show a surprising range of spin behavior, including a slingshot effect. Two or more particles can whip around each other in constant contact for several ‘orbits’ before disappearing in some wild acceleration. I’ve tried to slow it down, but this is first draft. I thought I could somehow mirror or extend the action to the collisions.
“I’ll Try This!” immediately resulted in very high equatorial velocities. Translational velocities are easily converted to spin, while I have no mechanism to shed spin except through collision. To paraphrase a colleague, spins are hard.
I took a break from Boids. A non-stop politics binge. I want to be sick.
So, back to subject. I’ll put a couple of thoughts out there.
Pretty as it is, Boids is still mostly charged points. The unexpected spin behavior is not real.
Starting where I'm at, I think I can model close particle interaction as pre-e/m strength changes along quadrature lines (30N/30S/30E/30W), radially expanding, where the time or charge density is also dependent on the equatorial velocity, etc.
That drives the total number of particles down but I’d rather see a few as accurately as possible at this point.
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
 Re: Simple Orbiter 2
Re: Simple Orbiter 2
Nevyn, Earlier in this thread, you shared your thoughts on the nature of tangential forces, https://milesmathis.forumotion.com/t128p15-simple-orbiter-2#991 :
On my next post https://milesmathis.forumotion.com/t128p15-simple-orbiter-2#996 I answered:
I hope you don't mind the delay. I’ve put a great deal of thought into the matter.
It really doesn’t matter whether the total number of photons equal antiphotons or not. The earth is structuring charge flow such that photon and antiphoton tangential velocities complement when delivering forces about the equatorial plane. They reinforce, not cancel, tangential velocities for bodies orbiting the spin axis.
My question, also, I’ve really enjoyed Miles’ latest paper, including this new - spin on structure (sorry), so I’ll cite it as well, “ The Stark Effect”, http://milesmathis.com/stark.pdf.
What is the mechanism that aligns the spin axis to maximize direct polar channeling? It seems to be present at all scales, from electrons to galaxies.
This leads me to make some speculations:
The sum of spin on the charge photons can sum to zero. The tangential force vector would then be zero and provide no tangential velocity to any orbiting bodies. Our solar system has a 2:1 ratio of photons to anti-photons so it does not sum to zero. Are there solar systems that do not orbit but just sort of sit there as deep into the charge field of their star as possible? Would all of the planets cause each other to move based on their charge interactions?
If the tangential force is caused by an imbalance of charge to anti-charge, then the force is applied at either the top or the bottom of the orbiting body, not over its complete shell. This is not a nice clean push sideways. I think it would cause spin to a stationary orbiter. Therefore, the existing axial spin of the orbiter resists that spin and applies it as a torque to the whole body. That is, part of the force is used up working against the axial spin and the other part is allowed to express itself so the result is a sideways force.
The axial spin must be driven or it would soon stop. I think the axial spin is caused by the charge flowing through the orbiting body (north/south through-charge). Therefore the charge is working against itself (not the exact same photon but the mass of charge effecting the orbiter at a given time). This may result as heat and help explain the internal and external heat of planets.
On my next post https://milesmathis.forumotion.com/t128p15-simple-orbiter-2#996 I answered:
Nevyn, Thanks for your previous post. You shared several points that beg consideration and discussion. Let me get back to that when I include spin.
I hope you don't mind the delay. I’ve put a great deal of thought into the matter.
Sure, in a given system, the number of photons compared to the number of anti-photons can be equal. Or say, far enough away, the total charges in a volume sums to zero. But that’s not correct. It ignores matter, or even net charge flow. The energy present, high or low, may be independent of that sum.The sum of spin on the charge photons can sum to zero.
Disagree. Consider Miles’ diagram. The one where photons enter the south pole and leave at some small positive latitude - up to 30 deg, and anti-photons enter the north pole and exit the earth south of the equator. (The image service is gone. Or it isn't working for me).The tangential force vector would then be zero and provide no tangential velocity to any orbiting bodies.
It really doesn’t matter whether the total number of photons equal antiphotons or not. The earth is structuring charge flow such that photon and antiphoton tangential velocities complement when delivering forces about the equatorial plane. They reinforce, not cancel, tangential velocities for bodies orbiting the spin axis.
And gravity too. I think so – absolutely. It’s a main premise of my model. If the sun were somehow plucked from the sky, our dominant objects, the gas giants would immediately begin to re-order the system.Would all of the planets cause each other to move based on their charge interactions?
I do not see this. Why would spin stop? Up or down photons entering their respective poles cause the same overall rotation direction. Granted, the spin is somehow tied to the energy level of the local charge field, but what determines a limit?The axial spin must be driven or it would soon stop.
I believe that the axial spin of the dominant body, our sun, is caused by charge recycling. The Earth’s axial spin depends mainly on the sun’s tangential forces.I think the axial spin is caused by the charge flowing through the orbiting body (north/south through-charge).
My question, also, I’ve really enjoyed Miles’ latest paper, including this new - spin on structure (sorry), so I’ll cite it as well, “ The Stark Effect”, http://milesmathis.com/stark.pdf.
At any temperature above zero, charge will create structure, both in itself and in any material, even a gas. To start with, the gas will align its poles to the applied field, to allow for better channeling at the atomic level.
What is the mechanism that aligns the spin axis to maximize direct polar channeling? It seems to be present at all scales, from electrons to galaxies.
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
 Re: Simple Orbiter 2
Re: Simple Orbiter 2
Hi Airman,
I have a quick response for you but I may need to flesh out these answers a bit later when I have more time.
Yes, it ignores matter because I was looking at the effects of charge on matter. If we wanted to find the total energy content then we would need to look at the matter present and factor that in but I was trying to look at what charge would do to the matter. I was only looking at the cause of the tangential vector, not what the vector is applied to. In that way, the sum of the spin on the charge photons can sum to zero and therefore there is no tangential force to cause a circular orbit.
But I was not looking at the equatorial force. That is (mostly) irrelevant to the orbital motion of the body itself and only applies to bodies that orbit it. I say mostly irrelevant because the equatorial charge emission does interact with the incoming charge (from the body we are orbiting) to cause magnetospheres, charge pauses, etc, which may limit the amount or direction of charge that actually reaches the orbiting body.
I was suggesting that the through-charge, and the equatorial emission to a lesser extent, causes the spin of the body not its tangential motion to that which it is orbiting. It is the action upon the body, by the charge passing through it, that causes the axial rotation of that body because each individual photon has some spin.
Yes, if we removed the sun then everything would adjust to orbit about jupiter (or possibly a jupiter and saturn binary system) but that isn't what I meant. I was thinking that an equal charge field (photons to anti-photons) would lead to no tangential forces for the orbiting bodies so they would find some equilibrium with all other bodies. This would leave them at a set distance from the central body but not circling around it.
In a vacumm, the spin would not stop, but these bodies are not in a vacumm. They are constantly bombarded with charge from the central body and each other. This would reduce the spin component over time. Since we do not see a reduction in the spin of orbiting bodies then it must be driven by something.
If it causes spin on the main body then it must cause spin on orbiting bodies as well. I don't see why it would only work for the larger body but not the smaller ones.
As I understand it, Miles has suggested that the suns tangential forces (from its emission) cause the circular motion (in conjunction with gravity and charge emission pushing it away) not the axial rotation, although it may be a factor in it.
I'm not sure of this mechanism myself. I probably need to read this paper again and see if I still agree with my speculation.
I have a quick response for you but I may need to flesh out these answers a bit later when I have more time.
LongtimeAirman wrote:Sure, in a given system, the number of photons compared to the number of anti-photons can be equal. Or say, far enough away, the total charges in a volume sums to zero. But that’s not correct. It ignores matter, or even net charge flow. The energy present, high or low, may be independent of that sum.Nevyn wrote:The sum of spin on the charge photons can sum to zero.
Yes, it ignores matter because I was looking at the effects of charge on matter. If we wanted to find the total energy content then we would need to look at the matter present and factor that in but I was trying to look at what charge would do to the matter. I was only looking at the cause of the tangential vector, not what the vector is applied to. In that way, the sum of the spin on the charge photons can sum to zero and therefore there is no tangential force to cause a circular orbit.
LongtimeAirman wrote:Disagree. Consider Miles’ diagram. The one where photons enter the south pole and leave at some small positive latitude - up to 30 deg, and anti-photons enter the north pole and exit the earth south of the equator. (The image service is gone. Or it isn't working for me).Nevyn wrote:The tangential force vector would then be zero and provide no tangential velocity to any orbiting bodies.
It really doesn’t matter whether the total number of photons equal antiphotons or not. The earth is structuring charge flow such that photon and antiphoton tangential velocities complement when delivering forces about the equatorial plane. They reinforce, not cancel, tangential velocities for bodies orbiting the spin axis.
But I was not looking at the equatorial force. That is (mostly) irrelevant to the orbital motion of the body itself and only applies to bodies that orbit it. I say mostly irrelevant because the equatorial charge emission does interact with the incoming charge (from the body we are orbiting) to cause magnetospheres, charge pauses, etc, which may limit the amount or direction of charge that actually reaches the orbiting body.
I was suggesting that the through-charge, and the equatorial emission to a lesser extent, causes the spin of the body not its tangential motion to that which it is orbiting. It is the action upon the body, by the charge passing through it, that causes the axial rotation of that body because each individual photon has some spin.
LongtimeAirman wrote:And gravity too. I think so – absolutely. It’s a main premise of my model. If the sun were somehow plucked from the sky, our dominant objects, the gas giants would immediately begin to re-order the system.Nevyn wrote:Would all of the planets cause each other to move based on their charge interactions?
Yes, if we removed the sun then everything would adjust to orbit about jupiter (or possibly a jupiter and saturn binary system) but that isn't what I meant. I was thinking that an equal charge field (photons to anti-photons) would lead to no tangential forces for the orbiting bodies so they would find some equilibrium with all other bodies. This would leave them at a set distance from the central body but not circling around it.
LongtimeAirman wrote:I do not see this. Why would spin stop? Up or down photons entering their respective poles cause the same overall rotation direction. Granted, the spin is somehow tied to the energy level of the local charge field, but what determines a limit?Nevyn wrote:The axial spin must be driven or it would soon stop.
In a vacumm, the spin would not stop, but these bodies are not in a vacumm. They are constantly bombarded with charge from the central body and each other. This would reduce the spin component over time. Since we do not see a reduction in the spin of orbiting bodies then it must be driven by something.
LongtimeAirman wrote:I believe that the axial spin of the dominant body, our sun, is caused by charge recycling. The Earth’s axial spin depends mainly on the sun’s tangential forces.Nevyn wrote:I think the axial spin is caused by the charge flowing through the orbiting body (north/south through-charge).
If it causes spin on the main body then it must cause spin on orbiting bodies as well. I don't see why it would only work for the larger body but not the smaller ones.
As I understand it, Miles has suggested that the suns tangential forces (from its emission) cause the circular motion (in conjunction with gravity and charge emission pushing it away) not the axial rotation, although it may be a factor in it.
LongtimeAirman wrote:
My question, also, I’ve really enjoyed Miles’ latest paper, including this new - spin on structure (sorry), so I’ll cite it as well, “ The Stark Effect”, http://milesmathis.com/stark.pdf.Mathis wrote:At any temperature above zero, charge will create structure, both in itself and in any material, even a gas. To start with, the gas will align its poles to the applied field, to allow for better channeling at the atomic level.
What is the mechanism that aligns the spin axis to maximize direct polar channeling? It seems to be present at all scales, from electrons to galaxies.
I'm not sure of this mechanism myself. I probably need to read this paper again and see if I still agree with my speculation.
 Re: Simple Orbiter 2
Re: Simple Orbiter 2
Thanks Nevyn. I do like your middle paragraph.
It’s exactly what I was asking for. A differentiation along the 30N/30S lines based upon relative resistance of a pole, as opposed to the general surface of the object. Miles also said that a pole provides a natural field “resistance”, paraphrasing again.
I think that’s close, aside from the first sentence conditional - I don’t believe an imbalance of up/down photons is necessary to generate pre-m tangential accelerations to a body in orbit. Also, I guess you’re talking gyroscopic torque.
Aligning spin poles to the charge field provides minimum resistance to the charge field lines. Minimum resistance makes more physical sense to me than "allow for better channeling", even though that is the result.
Definite aha moment!
If the tangential force is caused by an imbalance of charge to anti-charge, then the force is applied at either the top or the bottom of the orbiting body, not over its complete shell. This is not a nice clean push sideways. I think it would cause spin to a stationary orbiter. Therefore, the existing axial spin of the orbiter resists that spin and applies it as a torque to the whole body. That is, part of the force is used up working against the axial spin and the other part is allowed to express itself so the result is a sideways force.
It’s exactly what I was asking for. A differentiation along the 30N/30S lines based upon relative resistance of a pole, as opposed to the general surface of the object. Miles also said that a pole provides a natural field “resistance”, paraphrasing again.
I think that’s close, aside from the first sentence conditional - I don’t believe an imbalance of up/down photons is necessary to generate pre-m tangential accelerations to a body in orbit. Also, I guess you’re talking gyroscopic torque.
Aligning spin poles to the charge field provides minimum resistance to the charge field lines. Minimum resistance makes more physical sense to me than "allow for better channeling", even though that is the result.
Definite aha moment!
Last edited by LongtimeAirman on Fri Mar 18, 2016 10:30 pm; edited 2 times in total (Reason for editing : Cleaned up sentence begining: I think that's close; and Minimum resistance)
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
 Still no Angular Momentum
Still no Angular Momentum
.
I posted a gif of Boids showing a few slow bounces, elsewhere here recently, Re: Stacked Spins - scripting the photon's motion (technical), https://milesmathis.forumotion.com/t278p75-stacked-spins-scripting-the-photon-s-motion-technical#2915. It belongs here.
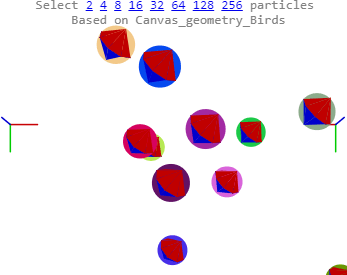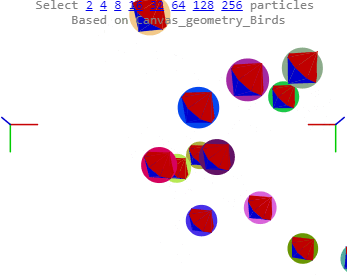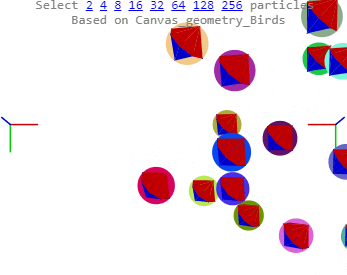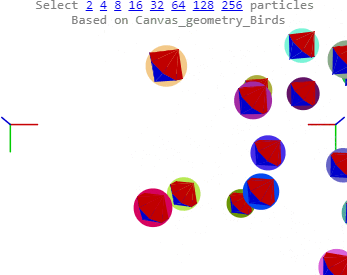
The spins aren’t included yet. I’ll make this a review and update with pretty new pictures.

Two positive spheres, magenta and green, with equal mass and length radii, traveling linearly in the direction of the spin axis (perfect spirals makes the example slightly simpler) in roughly opposing directions happen to meet. Each sphere contributes two direction/velocity vectors: 1) a Forward linear velocity - here, green or magenta - gF or mF; and 2) the tangential spin velocity at the collision Latitude - gL or mL. The gL and mL tangent velocity vectors are shown with their latitude sources.

The two tangential vectors gL and mL form the collision plane. Their cross product describes the perpendicular direction between the two colliding sphere centers. One must be able to determine whether angular exchange leads to a change in the spin rates or cause torque and precession – an adjustment to the forward direction - or if at light speed, begin an x spin tumble.
The gif shows that the bounce works. I’m still stuck at angular momentum - yes, going in circles. Oh, and programming – call that the lack of. Over the last two weeks I’ve enjoyed viewing many new three.js examples and updating from version 61 to 87 something, something permanent brain damage.
.
I posted a gif of Boids showing a few slow bounces, elsewhere here recently, Re: Stacked Spins - scripting the photon's motion (technical), https://milesmathis.forumotion.com/t278p75-stacked-spins-scripting-the-photon-s-motion-technical#2915. It belongs here.

The spins aren’t included yet. I’ll make this a review and update with pretty new pictures.

Two positive spheres, magenta and green, with equal mass and length radii, traveling linearly in the direction of the spin axis (perfect spirals makes the example slightly simpler) in roughly opposing directions happen to meet. Each sphere contributes two direction/velocity vectors: 1) a Forward linear velocity - here, green or magenta - gF or mF; and 2) the tangential spin velocity at the collision Latitude - gL or mL. The gL and mL tangent velocity vectors are shown with their latitude sources.

The two tangential vectors gL and mL form the collision plane. Their cross product describes the perpendicular direction between the two colliding sphere centers. One must be able to determine whether angular exchange leads to a change in the spin rates or cause torque and precession – an adjustment to the forward direction - or if at light speed, begin an x spin tumble.
The gif shows that the bounce works. I’m still stuck at angular momentum - yes, going in circles. Oh, and programming – call that the lack of. Over the last two weeks I’ve enjoyed viewing many new three.js examples and updating from version 61 to 87 something, something permanent brain damage.
.
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
 Re: Simple Orbiter 2
Re: Simple Orbiter 2
Great work, Airman. Keep it up. Don't worry about the programming. The only thing that matters is that it works! A programming language is just a tool like any other. It serves you. Experience brings finesse, but it is not required to get results.
 Re: Simple Orbiter 2
Re: Simple Orbiter 2
.
Thanks guys, no final conclusions yet. I'll need to dig deeper into the subject.
Nevyn have you made any progress studying gyroscopic math? Here's a picture with a couple of concerns.

Any comments are welcome.
.
Thanks guys, no final conclusions yet. I'll need to dig deeper into the subject.
Nevyn have you made any progress studying gyroscopic math? Here's a picture with a couple of concerns.

Any comments are welcome.
.
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
 Re: Simple Orbiter 2
Re: Simple Orbiter 2
I don't know about precession rotating about the collision point, but it seems that Miles said or implied that the higher level spin rotates around that point.
LloydK- Posts : 548
Join date : 2014-08-10
 Re: Simple Orbiter 2
Re: Simple Orbiter 2
I haven't looked at it in some time. The collision point is either the new point of rotation (for the new top spin level) or it is on the opposite side from that if you draw a line between the centers of the colliding particles. I lean towards the former, just because it is a real point where-as the other one is a bit more of a virtual point (as it might not even be on the BPhoton). On the other hand, that collision point is where we need to attach the new tangential velocity vector, which is not the same as the rotation point. So I like both for different reasons. Which is more real: the rotation point or the velocity point? When asked like that, I lean towards the velocity.
Reality is probably even trickier and something else entirely.
That doesn't help much, does it?
Maybe we need to work it in both directions and take the path of least resistance. That is, which one is easier to work with and calculate.
Reality is probably even trickier and something else entirely.
That doesn't help much, does it?
Maybe we need to work it in both directions and take the path of least resistance. That is, which one is easier to work with and calculate.
 Re: Simple Orbiter 2
Re: Simple Orbiter 2
When we study this, should we take into account the constant speed of light?
Ciaolo- Posts : 143
Join date : 2016-09-08
 Update
Update
.
Alrighty already, here's an update. I've spent most of my quality time during the last couple of weeks relearning and cleaning up Boids, I'm still very much a beginner. I removed all but a mention or two of the original bird flocking functions, such as wall avoidance. I admit I tend to include anything understood or not that can be reused or modified and am generally a slob. I apologize for having shared such a mess. In my defense, I’m concentrating on vectors. I’ve worked plenty of problems with matrices before, certainly in my Linear Algebra class (shudder) and others. One can easily read the scale, translation, rotation and more in a change matrix. I’m limiting myself to a straight vector solution if at all possible. The Euler axis/angle operation is perfectly acceptable.
I believe it’s fair to say I’m trying to model A-spin particle collisions at velocities well below light speed, but there are too many unknowns. I’m working with a given modeling space without a defined radius. It’s relatively confusing. For a given velocity - below c - the smaller the radius, the faster the particle. Each particle contributes gravity and charge inversely - the smaller the particle, the stronger the charge and weaker the gravity. At the smallest radius, photons do not emit charge and fly in straight lines, interrupted only by the occasional photon collision. Larger charged particles are subject to continuous charge accelerations and may travel in curved trajectories.
The model seems to match that, I can watch particles interact in complex loops or reduce or turn off the accelerations, leaving the particles simply bouncing in straight lines within a box, wraparound space or work out something else. I would implement the radius/tangential relationship Nevyn has written about; maybe we can tie gravity or charge magnitudes to the radius/spin frequency relationship. It’s just a tiny model but I would guess working with the magnitude scale changes between charged particles with any model would bring similar problems.
I agree that any collision precession below the speed of light would occur around the collision point, but then, in a collision, how can two simultaneous rotations precess around the same point independently? I appreciate the question between the collision center and center of the X-spin, again, precession is somehow involved. I agree that the top spin tangential or linear velocities of a particle (including a photon) can be much less than c, the X rotation may start off slow.
I'm still reviewing, but most of the collision vectors are drafted and ready. My immediate goal moving ahead with angular momentum is a wall bounce. Given a ball’s velocity, mass, composition, radius, surface friction, elasticity, gravity, etc., we are told that the angle of incidence equals the angle of reflection. That’s easily shown to be wrong when spin is involved. How exactly does spinning effect the bounce? I’m still not sure, since it involves some non-intuitive results. I’ll again refer you to Richard L. Garwin’s, “Kinematics of an Ultraelastic Rough Ball” *. The ultraelastic superball bounce is what I’ll shoot for. I have no problem accepting bounces since it seems to me that a particle bounce is equivalent to collision with the particle’s reflection - an anti-particle.
* The American Journal of Physics, vol. 37, no. 1, January 1969, Kinematics of an Ultraelastic Rough Ball http://www.rpi.edu/dept/phys/courses/PHYS1150/GarwinSuperBall.pdf
.
Alrighty already, here's an update. I've spent most of my quality time during the last couple of weeks relearning and cleaning up Boids, I'm still very much a beginner. I removed all but a mention or two of the original bird flocking functions, such as wall avoidance. I admit I tend to include anything understood or not that can be reused or modified and am generally a slob. I apologize for having shared such a mess. In my defense, I’m concentrating on vectors. I’ve worked plenty of problems with matrices before, certainly in my Linear Algebra class (shudder) and others. One can easily read the scale, translation, rotation and more in a change matrix. I’m limiting myself to a straight vector solution if at all possible. The Euler axis/angle operation is perfectly acceptable.
I believe it’s fair to say I’m trying to model A-spin particle collisions at velocities well below light speed, but there are too many unknowns. I’m working with a given modeling space without a defined radius. It’s relatively confusing. For a given velocity - below c - the smaller the radius, the faster the particle. Each particle contributes gravity and charge inversely - the smaller the particle, the stronger the charge and weaker the gravity. At the smallest radius, photons do not emit charge and fly in straight lines, interrupted only by the occasional photon collision. Larger charged particles are subject to continuous charge accelerations and may travel in curved trajectories.
The model seems to match that, I can watch particles interact in complex loops or reduce or turn off the accelerations, leaving the particles simply bouncing in straight lines within a box, wraparound space or work out something else. I would implement the radius/tangential relationship Nevyn has written about; maybe we can tie gravity or charge magnitudes to the radius/spin frequency relationship. It’s just a tiny model but I would guess working with the magnitude scale changes between charged particles with any model would bring similar problems.
I agree that any collision precession below the speed of light would occur around the collision point, but then, in a collision, how can two simultaneous rotations precess around the same point independently? I appreciate the question between the collision center and center of the X-spin, again, precession is somehow involved. I agree that the top spin tangential or linear velocities of a particle (including a photon) can be much less than c, the X rotation may start off slow.
I'm still reviewing, but most of the collision vectors are drafted and ready. My immediate goal moving ahead with angular momentum is a wall bounce. Given a ball’s velocity, mass, composition, radius, surface friction, elasticity, gravity, etc., we are told that the angle of incidence equals the angle of reflection. That’s easily shown to be wrong when spin is involved. How exactly does spinning effect the bounce? I’m still not sure, since it involves some non-intuitive results. I’ll again refer you to Richard L. Garwin’s, “Kinematics of an Ultraelastic Rough Ball” *. The ultraelastic superball bounce is what I’ll shoot for. I have no problem accepting bounces since it seems to me that a particle bounce is equivalent to collision with the particle’s reflection - an anti-particle.
* The American Journal of Physics, vol. 37, no. 1, January 1969, Kinematics of an Ultraelastic Rough Ball http://www.rpi.edu/dept/phys/courses/PHYS1150/GarwinSuperBall.pdf
.
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
 Another possible bounce
Another possible bounce
.
The latest. Another possible bounce.
Garwin’s ultraelastic rough ball bounce analysis above is limited to either the normal (perpendicular to the collision) or to the forward horizontal direction parallel to the collision. Ignoring details such as slip, slide or grip regimes, the forward direction includes the horizontal component of the forward motion as well as the ball’s equatorial spin tangential surface velocity, assumed parallel to the ball’s forward motion (as in rolling, top or bottom spin). I was left to speculate how Garwin might treat a more complicated case, and so came to focus on the collision vectors expressed either perpendicular or parallel to the ball’s spin axis; in which case any reflected deviation from the incident angle would be due to precession. But that would mean every particle loses energy with every bounce, as high velocities are converted to spin axis reorientations. Stuck again, but not idle, my mind flips between bounces and collisions regularly.
I went back through the papers looking for additional reference sources, and found a promising title - A classical experiment revisited: The bounce of balls and superballs in three dimensions. Am. J. Phys. 73, 28-36, 2005. I ended up at Research Gate requesting the paper. First thing Monday, I found the author, Antonio Doménech, had graciously e-mailed me a copy. I was immediately struck by the paper’s bounce schematic, again, very promising.

Vo, the hypotenuse vector on the left, is the ball’s initial velocity vector. Vo = Voz + Vox . Voz is related to the normal force Fn, the linear or vertical component of the bounce. The main collision component is Vox, the forward motion’s horizontal component, which will feel a frictional resistance of Ffx. The arbitrary spin of the ball is described by three rotations omega-x, omega-y, omega-z. Voy, has been added to account for the arbitrary spin – amounting to a y component of the ball’s tangential surface velocity just before contact; Voy is countered by the frictional force Ffy. The rebound vector is V. V = Vx + Vy + Vz.
The paper provides two fairly direct and simple sets of formulas in order to determine rebound for two different types of balls. Experiments were conducted to determine how well the two models predicted the outcome. Easy, right? Sorry, no; it’s not at all clear to me how one resolves an arbitrary spin into orthogonal x,y and z frequency components. Sounds like I'll need to include Euler angles.

Here’s the vector diagram (leaving out the angles for simplicity) when I bring in the latitudinal tangential spin velocity, Vs. Vs = Vsx + Vsy . Ffx must now counter Vox plus Vsx ; Ffy must counter Vsy . It’s not the form given in the paper, but it seems easy enough to try.
P.S. The vector lengths don't add in the image. I didn't want to lay Vsx on top of Ffx. Ffx is actually much shorter than shown since Vox and Vsx mostly cancel.
.
The latest. Another possible bounce.
Garwin’s ultraelastic rough ball bounce analysis above is limited to either the normal (perpendicular to the collision) or to the forward horizontal direction parallel to the collision. Ignoring details such as slip, slide or grip regimes, the forward direction includes the horizontal component of the forward motion as well as the ball’s equatorial spin tangential surface velocity, assumed parallel to the ball’s forward motion (as in rolling, top or bottom spin). I was left to speculate how Garwin might treat a more complicated case, and so came to focus on the collision vectors expressed either perpendicular or parallel to the ball’s spin axis; in which case any reflected deviation from the incident angle would be due to precession. But that would mean every particle loses energy with every bounce, as high velocities are converted to spin axis reorientations. Stuck again, but not idle, my mind flips between bounces and collisions regularly.
I went back through the papers looking for additional reference sources, and found a promising title - A classical experiment revisited: The bounce of balls and superballs in three dimensions. Am. J. Phys. 73, 28-36, 2005. I ended up at Research Gate requesting the paper. First thing Monday, I found the author, Antonio Doménech, had graciously e-mailed me a copy. I was immediately struck by the paper’s bounce schematic, again, very promising.

Vo, the hypotenuse vector on the left, is the ball’s initial velocity vector. Vo = Voz + Vox . Voz is related to the normal force Fn, the linear or vertical component of the bounce. The main collision component is Vox, the forward motion’s horizontal component, which will feel a frictional resistance of Ffx. The arbitrary spin of the ball is described by three rotations omega-x, omega-y, omega-z. Voy, has been added to account for the arbitrary spin – amounting to a y component of the ball’s tangential surface velocity just before contact; Voy is countered by the frictional force Ffy. The rebound vector is V. V = Vx + Vy + Vz.
The paper provides two fairly direct and simple sets of formulas in order to determine rebound for two different types of balls. Experiments were conducted to determine how well the two models predicted the outcome. Easy, right? Sorry, no; it’s not at all clear to me how one resolves an arbitrary spin into orthogonal x,y and z frequency components. Sounds like I'll need to include Euler angles.

Here’s the vector diagram (leaving out the angles for simplicity) when I bring in the latitudinal tangential spin velocity, Vs. Vs = Vsx + Vsy . Ffx must now counter Vox plus Vsx ; Ffy must counter Vsy . It’s not the form given in the paper, but it seems easy enough to try.
P.S. The vector lengths don't add in the image. I didn't want to lay Vsx on top of Ffx. Ffx is actually much shorter than shown since Vox and Vsx mostly cancel.
.
Last edited by LongtimeAirman on Wed Oct 25, 2017 8:41 pm; edited 2 times in total (Reason for editing : Added PS)
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
 Stuck at the Controls
Stuck at the Controls
.
Sorry, no oblique bounce progress to report. I wish I could say I’ve been taking a break; instead, I’ve been tied up in Threejs, JavaScript and HTML controls, every day, many hours since my last post. I’ve been studying the subject and tinkering with the program. My understanding has improved, but not well enough, I’m afraid of dropping dead before it’s done.
Nevyn, Please help. I hope you don’t mind the imposition, I’m still embarrassed from last time. I have every intention of improving this project and I’m otherwise extremely happy with it. There’s plenty of opportunity to work with the physics and the faster we can come up with an acceptable product the better to explore collisions in detail. Ideally, eventually, I hope you see fit to adopt it, and include it on your site, unless of course you’ve created your own collision model. In any case, please don’t hesitate to do your best on my account.
As you know, most of the code for this GravityAndChargeFieldDemo (Boids) started as canvas_geometry_birds, https://threejs.org/examples/#canvas_geometry_birds (c_g_t ) - just flocking birds, no control keys required. I modified c_g_t by copying the HTML hash control for the number of particles from webgl_gpgpu_birds, https://threejs.org/examples/#webgl_gpgpu_birds, (w_g_b). w_g_b makes very little sense to me.
There are several other variables in Boids: scale (or particle radius), wallBounce or wraparound, various grids, and particle appearance (sprites or marbles). I change those variables from inside the .html file. That’s unacceptable, so I’ve been trying to add user controls.
I’ve begun to copy the set of HTML controls from https://threejs.org/examples/#webgl_geometry_text, (w_g_t), but the hashtable/control structure has frustrated the beegeebers out of me.
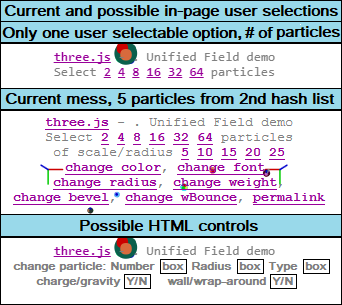
I haven’t made any progress in dat.gui.min.js controls either, since the mousedrag event belongs to the OrbitControls camera. I cannot adjust a slider – the scene moves instead. I suppose the dat.gui could work if it were limited to just buttons and not slide bars. A possible fix -
Sending the code in a separate pm.
.
Sorry, no oblique bounce progress to report. I wish I could say I’ve been taking a break; instead, I’ve been tied up in Threejs, JavaScript and HTML controls, every day, many hours since my last post. I’ve been studying the subject and tinkering with the program. My understanding has improved, but not well enough, I’m afraid of dropping dead before it’s done.
Nevyn, Please help. I hope you don’t mind the imposition, I’m still embarrassed from last time. I have every intention of improving this project and I’m otherwise extremely happy with it. There’s plenty of opportunity to work with the physics and the faster we can come up with an acceptable product the better to explore collisions in detail. Ideally, eventually, I hope you see fit to adopt it, and include it on your site, unless of course you’ve created your own collision model. In any case, please don’t hesitate to do your best on my account.
As you know, most of the code for this GravityAndChargeFieldDemo (Boids) started as canvas_geometry_birds, https://threejs.org/examples/#canvas_geometry_birds (c_g_t ) - just flocking birds, no control keys required. I modified c_g_t by copying the HTML hash control for the number of particles from webgl_gpgpu_birds, https://threejs.org/examples/#webgl_gpgpu_birds, (w_g_b). w_g_b makes very little sense to me.
There are several other variables in Boids: scale (or particle radius), wallBounce or wraparound, various grids, and particle appearance (sprites or marbles). I change those variables from inside the .html file. That’s unacceptable, so I’ve been trying to add user controls.
I’ve begun to copy the set of HTML controls from https://threejs.org/examples/#webgl_geometry_text, (w_g_t), but the hashtable/control structure has frustrated the beegeebers out of me.

I haven’t made any progress in dat.gui.min.js controls either, since the mousedrag event belongs to the OrbitControls camera. I cannot adjust a slider – the scene moves instead. I suppose the dat.gui could work if it were limited to just buttons and not slide bars. A possible fix -
I don't see how to apply it. I suppose my control variables aren't set up properlyIf you use a mouse-controlled camera with the dat.gui.min control panel, you have to comment the following line in the MouseListener of the mouseDown action - event.preventDefault();
Sending the code in a separate pm.
.
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
 Re: Simple Orbiter 2
Re: Simple Orbiter 2
Do you want me to add controls to manipulate those values? I can do that and document it more thoroughly than I normally would so that you can see what is going on and how to add to and alter it yourself (along with a bit of research, probably). I will use basic HTML/JS code at first. Later, when you are comfortable with that, I can show you how to make it look prettier with little change (just the controls, it won't change the ThreeJS parts).
I will look over the physics as well and see how it lines up with my own thoughts on the subject.
I will look over the physics as well and see how it lines up with my own thoughts on the subject.
 Re: Simple Orbiter 2
Re: Simple Orbiter 2
.
Thanks Nevyn, yes, just add additional controls so anyone can change them, that would be great.
I'm still worried whether you see it operating properly or not. I may need to explain a variable or two.
In the diagram I show (box). (box) can be a pull down list.
I'd like to discuss any physics objections you may have, or at least give my understanding. I've provided plenty of comments. There are factorial numbers of accelerations/calculations going on, the program is a pig, but it's a pretty pig.
.
Thanks Nevyn, yes, just add additional controls so anyone can change them, that would be great.
I'm still worried whether you see it operating properly or not. I may need to explain a variable or two.
In the diagram I show (box). (box) can be a pull down list.
I'd like to discuss any physics objections you may have, or at least give my understanding. I've provided plenty of comments. There are factorial numbers of accelerations/calculations going on, the program is a pig, but it's a pretty pig.
.
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
Page 1 of 2 • 1, 2 
Page 1 of 2
Permissions in this forum:
You cannot reply to topics in this forum