Re: Proof that pi=4

by **Jared Magneson** Tue Nov 01, 2016 3:56 pm

Yeah, sorry about that cycloid mess-up. I was so deep into it that I wasn't checking my math and time variables, got confused. I'll delete that shortly and replace it with the proper timing, etc..

I love that animated .GIF! Works great, thanks for doing that. I honestly just didn't feel like tossing it into Photoshop or whatever (kinda tedious, from Maya) and glad you beat me to it in this case.

by **LongtimeAirman** Tue Nov 01, 2016 4:23 pm

.

We turned a page, so I'll put it at the top.
.

by soostdijk Mon Nov 07, 2016 4:49 pm

LongtimeAirman wrote:
I believe that Steven said the ball in the curve "banks a few tens of degrees". I currently interpret that "fact" to mean that we can replace the circular track with large radius gently concave surface, like a shallow serving bowl. If we were accurate enough, a gently banked steel ribbon along a plate's rim would work just as well. Simply replacing the steel balls with patterned glass marbles would show that there weren't any additional rotations present; the experimental velocities may vary, but the outcome would remain the same. It's still fun.

The ball in the curve banks a few tens of degrees because the circular path has the centripetal force next to gravity while the straight path has only gravity.
I made some detailed video's of the banking to see if that could prove whether Miles formula a=v^2/2r or Newtons formula a=v^2/r is correct, but the difference between 20 degrees or 40 degrees was too hard to determine from a side view. Perhaps it can be determined more accurately with a half-circle setup. The banking was in the order of 20-40 degrees though, which was consistent with both formula's. Sometimes the banking was oscillating, guess that had to do with how the ball enters the circular path. The oscillation did not seem to affect the outcome.

by **LongtimeAirman** Mon Nov 07, 2016 8:59 pm

soostdijk wrote. The ball in the curve banks a few tens of degrees because the circular path has the centripetal force next to gravity while the straight path has only gravity.

airman. I agree. I hadn’t worked with any centripetal force ‘analysis’, and so I avoided the subject, making the general observation to the effect that the additional track length due to banking was insignificant compared to the 20% distance increase of the curved motion metric.

Steven, Welcome. Congratulations for demonstrating the new motion metric, pi=4.

You’ve answered many comments, good and bad, again and again. I’m surprised that some people will not see the new metric, insisting (despite the evidence) that the ball is slower in the circular track. Could you share some thoughts on the reactions to your experiment?

Your circular and straight tracks are elegant, sufficient and necessary to prove the motion metric. One complaint is the inability to monitor final velocities. After our site discussion above, I (Robert M) left a comment at the top of your short video comments section pointing out the obvious. The discussion occurred at the long video. You’ve mentioned track alternatives versus the seasonal lack of sunlight. Any updates there?

soostdijk wrote. I made some detailed video's of the banking to see if that could prove whether Miles formula a=v^2/2r or Newtons formula a=v^2/r is correct, but the difference between 20 degrees or 40 degrees was too hard to determine from a side view. Perhaps it can be determined more accurately with a half-circle setup. The banking was in the order of 20-40 degrees though, which was consistent with both formula's. Sometimes the banking was oscillating, guess that had to do with how the ball enters the circular path. The oscillation did not seem to affect the outcome.

I assumed a rolling contact. How can oscillations occur? Good, unexpected extra data.

I became wrapped up in a 180 twist along the length of the 360deg pvc loop track – a spiraling tangent, but that has nothing to do with the motion metric.

Given your breakthrough, I was delighted to post at TBolts as your proponent. I wasn’t good enough to carry off a winning angular momentum argument and so had mainly avoided that subject too. Nevertheless, I think the crowd there is ready for you.

I'm convinced your work makes our future brighter.
.

by soostdijk Tue Nov 08, 2016 6:48 am

LongtimeAirman wrote:
soostdijk wrote. The ball in the curve banks a few tens of degrees because the circular path has the centripetal force next to gravity while the straight path has only gravity.
airman. I agree. I hadn’t worked with any centripetal force ‘analysis’, and so I avoided the subject, making the general observation to the effect that the additional track length due to banking was insignificant compared to the 20% distance increase of the curved motion metric.

Steven, Welcome. Congratulations for demonstrating the new motion metric, pi=4.

Thanks for the welcome and the kind words. Credit where credit is due, I got the idea through Miles from his description of Jeff's experiment with the toy trains. I did some experiments with electricity tube and metal balls to convince myself and was lucky to find the transparent PVC tubing so it could be shown in a clear video. I'm an engineer, like to make things work, happy to be able to help Miles here.

LongtimeAirman wrote:You’ve answered many comments, good and bad, again and again. I’m surprised that some people will not see the new metric, insisting (despite the evidence) that the ball is slower in the circular track. Could you share some thoughts on the reactions to your experiment?

Question: is the ball really slower? That is what most people cannot get their head around (including me Smile

). You mention a new "metric", but that is a bit too mainstream for me. People have been confused into thinking that there are three orthogonal axes with an arbitrary origin spanning space, but distance and time are both derived from motion, so we first have to understand motion better.
Think we have to start there by updating our understanding on momentum. The momentum of the ball seems to change instantly and is conserved around the circular motion. That is both curious.
I have also done the experiment with the 180 degree circle setup and then the exit velocity of the circular ball is 3.14/4 of the entry velocity, so the "b" momentum as you call it is then lost. It is logical as the tube cannot deliver a pushing force, only a restrictive force, but as long as we cannot show without doubt what happens with the momentum of the ball at entry and exit I will not post it. Let people absorb this experiment first.

LongtimeAirman wrote:Your circular and straight tracks are elegant, sufficient and necessary to prove the motion metric. One complaint is the inability to monitor final velocities. After our site discussion above, I (Robert M) left a comment at the top of your short video comments section pointing out the obvious. The discussion occurred at the long video. You’ve mentioned track alternatives versus the seasonal lack of sunlight. Any updates there?
soostdijk wrote. I made some detailed video's of the banking to see if that could prove whether Miles formula a=v^2/2r or Newtons formula a=v^2/r is correct, but the difference between 20 degrees or 40 degrees was too hard to determine from a side view. Perhaps it can be determined more accurately with a half-circle setup. The banking was in the order of 20-40 degrees though, which was consistent with both formula's. Sometimes the banking was oscillating, guess that had to do with how the ball enters the circular path. The oscillation did not seem to affect the outcome.
I assumed a rolling contact. How can oscillations occur? Good, unexpected extra data.

For the updates see above.

About the oscillations, think they happen if the spin of the ball is not aligned closely with the curving of the tube so the ball overshoots.

LongtimeAirman wrote:I became wrapped up in a 180 twist along the length of the 360deg pvc loop track – a spiraling tangent, but that has nothing to do with the motion metric.

Given your breakthrough, I was delighted to post at TBolts as your proponent. I wasn’t good enough to carry off a winning angular momentum argument and so had mainly avoided that subject too. Nevertheless, I think the crowd there is ready for you.

I'm convinced your work makes our future brighter.
.

TB might be ready but I do not have time to waste on trolls Wink

by soostdijk Tue Nov 08, 2016 5:14 pm

LongtimeAirman wrote:
Given your breakthrough, I was delighted to post at TBolts as your proponent. I wasn’t good enough to carry off a winning angular momentum argument and so had mainly avoided that subject too. Nevertheless, I think the crowd there is ready for you.

I waded through the insults on the TB forum to see if there is anything that I could clarify but I think it all has been done excellently by you already.

There is two things I could suggest to mention in the discussion:

1. Pulling a "velocity" around a circle is not the same as pulling a solid ruler around a circle. The velocity vector will need to be rotated along the path otherwise it would not follow the path. This rotation takes time. So it would not be logical that the length of a circular path measured with a velocity would be the same as measured with a ruler. For all these people shouting that Pi will always remain 3.14, sure, but only for geometric ratios.

2. There was a discussion whether the definition of length would need to change but that is not the case. Measuring the length of the circular path starting with the origin on the path will yield 4 as is shown in the video. It would yield 3.14 measured from the virtual center but only if you ignore the rotating reference frame of the ball (which is interestingly enough actually admitted by the mainstream Smile

).

by **LongtimeAirman** Tue Nov 08, 2016 9:06 pm

soostdijk wrote. I waded through the insults on the TB forum to see if there is anything that I could clarify but I think it all has been done excellently by you already.

There is two things I could suggest to mention in the discussion:

1. Pulling a "velocity" around a circle is not the same as pulling a solid ruler around a circle. The velocity vector will need to be rotated along the path otherwise it would not follow the path. This rotation takes time. So it would not be logical that the length of a circular path measured with a velocity would be the same as measured with a ruler. For all these people shouting that Pi will always remain 3.14, sure, but only for geometric ratios.

2. There was a discussion whether the definition of length would need to change but that is not the case. Measuring the length of the circular path starting with the origin on the path will yield 4 as is shown in the video. It would yield 3.14 measured from the virtual center but only if you ignore the rotating reference frame of the ball (which is interestingly enough actually admitted by the mainstream ).

airman. Thanks for the positive review. Obviously I was learning during the discussion. Debating trolls with slowly improving arguments may not be ideal but it works.

You’re right. I haven’t considered the “rotating reference frame of the ball” and how it’s necessary to properly calculate the motion distance. I will do so.

I also need to spend a great deal more time examining the angular velocity aspect. How many degrees of banking differentiates Newton’s from Miles’ formulas?

Of course, truth be told, we’ve had our own discussions here. Nevyn gave me the confidence to take on TB with the rate*time=distance argument; keeping it simple. I’m sure he’s ready for a rotating frame reference discussion.
.

by **LongtimeAirman** Fri Nov 11, 2016 11:48 am

.
Another Update to pi7
http://milesmathis.com/pi7.pdf

Miles wrote. November 8, 2016: I have had one of my online buddies create a gif for me that matches part of the
video they are suppressing. I have never imported a gif into a paper before, so hopefully this will
work, including the motion. See below.

If that doesn't move for you, you can go to his video at Vimeo

Jared, At this point we have a cheer (please forgive the fact that it's military). It goes,

HooAhh

The rest of the update is an eye-opener too.
.

by **LongtimeAirman** Sat Nov 26, 2016 6:54 pm

.
The materials:

Proof that pi=4 - Page 2 Catfoo11

CatFoodClampHosedCakeContainer.

Proof that pi=4 - Page 2 Abovet11

By some quirk, my working diameter is 31.4cm.
.

by **LongtimeAirman** Fri Dec 02, 2016 10:55 pm

.
Steven O was careful to keep his ramp support structure outside his youtube video image. I can understand why, it's a distraction from the pi=4 demonstration. Hiding it only works once. I must improvise something - Oogly.
Proof that pi=4 - Page 2 Rampas10

A height adjustable ramp support structure.
Proof that pi=4 - Page 2 Rampas13

I haven’t cut the track lengths yet. One can easily straighten coiled pvc using rope. Start with a feather (or steel ball), and thread. Or ask an electrician.
Proof that pi=4 - Page 2 Rampas11

Thank you Serendipity, all but the steel 5/8X8in bolt, washers and nuts were in my junk box. Only the threaded U bolts’ half circle needs improving/modifying. The U bolts clamps’ slightly concave/convex surfaces allow plenty of smooth controlled swivel about the tripod’s leg angle changes with little pvc pinching. An old plumbing coupler is used here as a heavy spacer to get past the bolt’s shank. The release mechanism must be here somewhere.
Proof that pi=4 - Page 2 Rampas12

I'm grateful for the distraction.
.

by **LongtimeAirman** Fri Dec 09, 2016 7:55 pm

.

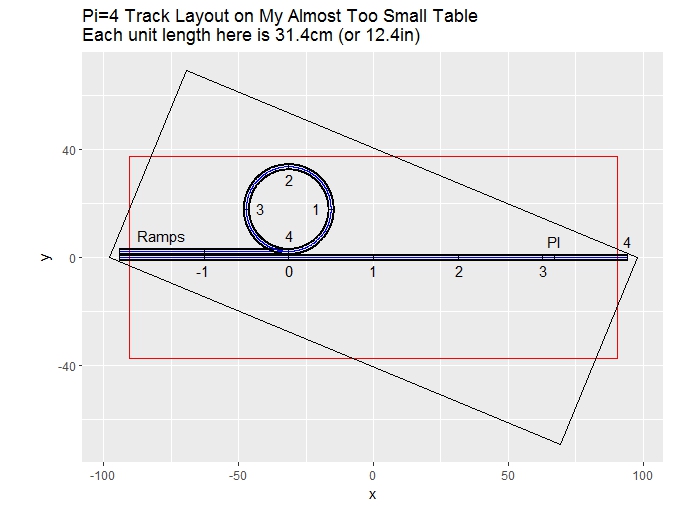
The following R code is submitted for your approval.

HINT - Feedback is greatly appreciated.

Code:: library(ggplot2) ###################################### ## ## ## Pi=4 ## ## ## ###################################### ## Intended to recreate ## ## Steven Oostdijk's ## ## Pi=4 experiment as described in ## ## http://milesmathis.com/pi7.pdf ## ## -------------------------------- ## ## Posted at ## ## http://milesmathis.forumotion.com/ ## ## -------------------------------- ## ## Contributing to a future ## ## Miles Mathis R project ## ###################################### ## Input data used: ## ## 1) The unit circle's diameter ## ## 2) InsideTrackWidth ## ## 3) OutsideTrackWidth ## ## 4) Table length and width ## ## -------------------------------- ## ## Replace with your data to ## ## plot your own tracks ## ## -------------------------------- ## ## measurements in cm ## ## unless noted otherwise ## ###################################### ## The tracklengths are scaled ## to the working diameter ## CHANGE a_diameter HERE a_diameter <- 31.4 a <- a_diameter a_diaInInches <- a_diameter/2.54 a_diaInInches ## [1] 12.3622 ## CHANGE INSIDE AND OUTSIDE DIAMETERS HERE ## The pvc inside diameter is the trackWidthIn. ## 5/8" converted to centimeters b_trackWidthIn <- 2.54*(5/8) bi <- b_trackWidthIn ## The pvc outside diameter is the trackWidthOut. ## 7/8" converted to centimeters b_trackWidthOut <- 2.54*(7/8) bo <- b_trackWidthOut ## The circle track length, 0-4, is the circular ## track's centerline circumference c_circumference <- 3.14159*a_diameter c314 <- c_circumference ## c314=98.6459 ## The radii needed to plot the circular track: ## 14.590, 14.910, 15.700, 16.490, 16.810 (sorted) r <- a_diameter/2 rOut <- r + bo/2 rIn <- r - bo/2 rOut2 <- r + bi/2 rIn2 <- r - bi/2 ## For rough (unknown ramp) overall length estimate, ## the total length will be: ## 1) ramp(a_diameter), 2)initNegOneToZero(a_diameter), ## and 3) straight track length (4*a_diameter). ## A total rough estimate plot length of 6*a_diameter d_straight <- 6*a_diameter ## d_straight = 188.4 ## CHANGE TABLE DIMENSIONS (T1 and T2) HERE ## My workspace limit, table dimensions, is 29.5X71.25in. ## Convert to cm. T1 <- 29.5*2.54 ## T1 = 74.93 T2 <- 71.25*2.54 ## T2 = 180.975 xCoordsInit <- c(-T2/2,-T2/2,T2/2,T2/2,-T2/2) yCoordsInit <- c(-T1/2,T1/2,T1/2,-T1/2,-T1/2) ## With a_diameter=31.4, d_straight = 188.4 > T2 = 180.975. ## I've exceeded my table length limit by a few centimeters. ## I can gain some centimeters by aligning the straight ## track to the table's diagonal. ## For my special case, to determine a diagonal layout ## Calculate table rotation MyTable <- cbind(xCoordsInit,yCoordsInit) MyTable ## xCoordsInit yCoordsInit ##[1,] -90.4875 -37.465 ##[2,] -90.4875 37.465 ##[3,] 90.4875 37.465 ##[4,] 90.4875 -37.465 ##[5,] -90.4875 -37.465 ## Rotation angle equals neg arcTan((T1/2)/(T2/2)) ## = neg arcTan(37.465/90.4875) Angle <- (-1)*atan(T1/T2) ## Angle in radians Angle ## -0.3925... AngInDeg <- Angle*360/(2*3.14159) AngInDeg ## -22.49deg ## x'<- x*cos(theta)+ysin(theta) ## y'<- x*(-1)sin(theta)+ycos(theta) ZRotation <- matrix(c(cos(Angle),sin(Angle),(-1)*sin(Angle),cos(Angle)),nrow = 2,ncol = 2,byrow = TRUE) ZRotation dim(MyTable) TR <- MyTable%*%ZRotation TR ## [,1] [,2] ##[1,] -97.93679 0.00000 ##[2,] -69.27286 69.23066 ##[3,] 97.93679 0.00000 ##[4,] 69.27286 -69.23066 ##[5,] -97.93679 0.00000 ## I need a better way to transfer both table contents, ## (initial and final) for the ggplot geom_path function. xCoordsFinal <- c(-97.93678513/2,-69.27286231/2,97.93678513/2,69.27286231/2,-97.93678513/2) yCoordsFinal <- c(-0,69.23066104,0,-69.23066104,-0) ## plot(xCoordsFinal,yCoordsFinal) ## The ramp's horiz distance must be under 31.4cm to ## gain any more cm's. It's looking ugly for Oogly. ggplot(data=data.frame(x=1,y=1),aes(x,y))+ ggtitle("Pi=4 Track Layout on My Almost Too Small Table\nEach unit length here is 31.4cm (or 12.4in)")+ ## tabletop: geom_path(data=data.frame(x=c(-T2/2,-T2/2,T2/2,T2/2,-T2/2),y=c(-T1/2,T1/2,T1/2,-T1/2,-T1/2)), colour = "Red")+ geom_path(data=data.frame(x=c(TR[1,1],TR[2,1],TR[3,1],TR[4,1],TR[5,1]),y=c(TR[1,2],TR[2,2],TR[3,2],TR[4,2],TR[5,2])))+ ## Track Centerlines are blue ## ramps: ## circle track geom_path(data=data.frame(x=c(-3*a,-2*a),y=c(bo,bo)), colour = "Blue")+ geom_path(data=data.frame(x=c(-3*a,-2*a,-2*a,-3*a,-3*a),y=c(bo/2,bo/2,1.5*bo,1.5*bo,bo/2)))+ geom_path(data=data.frame(x=c(-3*a,-2*a,-2*a,-3*a,-3*a),y=c(bo+bi/2 ,bo+bi/2,bo-bi/2,bo-bi/2,bo+bi/2)))+ ## straight track geom_path(data=data.frame(x=c(-3*a,-2*a),y=c(0,0)), colour = "Blue")+ geom_path(data=data.frame(x=c(-3*a,-2*a,-2*a,-3*a,-3*a),y=c(bo/2,bo/2,-bo/2,-bo/2,bo/2)))+ geom_path(data=data.frame(x=c(-3*a,-2*a,-2*a,-3*a,-3*a),y=c(0+bi/2,0+bi/2,0-bi/2,0-bi/2,0+bi/2)))+ annotate("text", x = -2.5*a, y = 8, label = "Ramps") + annotate("text", x = -63, y = -5, label = "-1") + ## NegOneToZero: ## circle track geom_path(data=data.frame(x=c(-2*a,-1*a),y=c(bo,bo)), colour = "Blue")+ geom_path(data=data.frame(x=c(-2*a,-1*a,-1*a,-2*a,-2*a),y=c(bo/2,bo/2,1.5*bo,1.5*bo,bo/2)))+ geom_path(data=data.frame(x=c(-2*a,-1*a,-1*a,-2*a,-2*a),y=c(bo+bi/2,bo+bi/2,bo-bi/2,bo-bi/2,bo+bi/2)))+ ## straight track geom_path(data=data.frame(x=c(-2*a,-1*a),y=c(0,0)), colour = "Blue")+ geom_path(data=data.frame(x=c(-2*a,-1*a,-1*a,-2*a,-2*a),y=c(bo/2,bo/2,-bo/2,-bo/2,bo/2)))+ geom_path(data=data.frame(x=c(-2*a,-1*a,-1*a,-2*a,-2*a),y=c(0+bi/2,0+bi/2,0-bi/2,0-bi/2,0+bi/2)))+ annotate("text", x = -31, y = -5, label = "0") + ## ZeroToOne: ## circle track geom_path(data=data.frame(x=c(-1*a+(15700:(0)/1000),-1*a),y=c((15.7+bo)-sqrt((15.7)^2-c(15700:(0)/1000,0)^2))),aes(x=x,y=y), colour = "Blue")+ geom_path(data=data.frame(x=c(-1*a+(14590:(0)/1000),-1*a),y=c((15.7+bo)-sqrt((14.59)^2-c(14590:(0)/1000,0)^2))),aes(x=x,y=y))+ geom_path(data=data.frame(x=c(-1*a+(16490:(0)/1000),-1*a),y=c((15.7+bo)-sqrt((16.49)^2-c(16490:(0)/1000,0)^2))),aes(x=x,y=y))+ geom_path(data=data.frame(x=c(-1*a+(16810:(0)/1000),-1*a),y=c((15.7+bo)-sqrt((16.81)^2-c(16810:(0)/1000,0)^2))),aes(x=x,y=y))+ geom_path(data=data.frame(x=c(-1*a+(14910:(0)/1000),-1*a),y=c((15.7+bo)-sqrt((14.91)^2-c(14910:(0)/1000,0)^2))),aes(x=x,y=y))+ geom_path(data=data.frame(x=c(-1*a+14.59,-1*a+16.81),y=c(15.7+bo,15.7+bo)))+ annotate("text", x = -21, y = 18, label = "1") + ## straight track geom_path(data=data.frame(x=c(-1*a,0*a),y=c(0,0)), colour = "Blue")+ geom_path(data=data.frame(x=c(-1*a,0*a,0*a,-1*a,-1*a),y=c(bo/2,bo/2,-bo/2,-bo/2,bo/2)))+ geom_path(data=data.frame(x=c(-1*a,0*a,0*a,-1*a,-1*a),y=c(0+bi/2,0+bi/2,0-bi/2,0-bi/2,0+bi/2)))+ annotate("text", x = 0, y = -5, label = "1") + ## OneToTwo: ## circle track geom_path(data=data.frame(x=c(-1*a+(15700:(0)/1000),-1*a),y=c((15.7+bo)+sqrt((15.7)^2-c(15700:(0)/1000,0)^2))),aes(x=x,y=y), colour = "Blue")+ geom_path(data=data.frame(x=c(-1*a+(14590:(0)/1000),-1*a),y=c((15.7+bo)+sqrt((14.59)^2-c(14590:(0)/1000,0)^2))),aes(x=x,y=y))+ geom_path(data=data.frame(x=c(-1*a+(16490:(0)/1000),-1*a),y=c((15.7+bo)+sqrt((16.49)^2-c(16490:(0)/1000,0)^2))),aes(x=x,y=y))+ geom_path(data=data.frame(x=c(-1*a+(16810:(0)/1000),-1*a),y=c((15.7+bo)+sqrt((16.81)^2-c(16810:(0)/1000,0)^2))),aes(x=x,y=y))+ geom_path(data=data.frame(x=c(-1*a+(14910:(0)/1000),-1*a),y=c((15.7+bo)+sqrt((14.91)^2-c(14910:(0)/1000,0)^2))),aes(x=x,y=y))+ geom_path(data=data.frame(x=c(-1*a,-1*a),y=c(31.4+bo/2,2*16.81+bo/2)))+ annotate("text", x = -31, y = 29, label = "2") + ## straight track geom_path(data=data.frame(x=c(0,a),y=c(0,0)), colour = "Blue")+ geom_path(data=data.frame(x=c(0,a,a,0*a,0*a),y=c(bo/2,bo/2,-bo/2,-bo/2,bo/2)))+ geom_path(data=data.frame(x=c(0,a,a,0*a,0*a),y=c(0+bi/2 ,0+bi/2,0-bi/2,0-bi/2,0+bi/2)))+ annotate("text", x = 32, y = -5, label = "2") + ## TwoToThree: ## circle track geom_path(data=data.frame(x=c(-1*a-(15700:(0)/1000),-1*a),y=c((15.7+bo)+sqrt(15.7^2-c(15700:(0)/1000,0)^2))),aes(x=x,y=y), colour = "Blue")+ geom_path(data=data.frame(x=c(-1*a-(14590:(0)/1000),-1*a),y=c((15.7+bo)+sqrt((14.59)^2-c(14590:(0)/1000,0)^2))),aes(x=x,y=y))+ geom_path(data=data.frame(x=c(-1*a-(16490:(0)/1000),-1*a),y=c((15.7+bo)+sqrt((16.49)^2-c(16490:(0)/1000,0)^2))),aes(x=x,y=y))+ geom_path(data=data.frame(x=c(-1*a-(16810:(0)/1000),-1*a),y=c((15.7+bo)+sqrt((16.81)^2-c(16810:(0)/1000,0)^2))),aes(x=x,y=y))+ geom_path(data=data.frame(x=c(-1*a-(14910:(0)/1000),-1*a),y=c((15.7+bo)+sqrt((14.91)^2-c(14910:(0)/1000,0)^2))),aes(x=x,y=y))+ geom_path(data=data.frame(x=c(-1*a-14.59,-1*a-16.81),y=c(15.7+bo,15.7+bo)))+ annotate("text", x = -42, y = 18, label = "3") + ## straight track geom_path(data=data.frame(x=c(a,2*a),y=c(0,0)), colour = "Blue")+ geom_path(data=data.frame(x=c(a,2*a,2*a,a,a),y=c(bo/2,bo/2,-bo/2,-bo/2,bo/2)))+ geom_path(data=data.frame(x=c(a,2*a,2*a,a,a),y=c(0+bi/2 ,0+bi/2,0-bi/2,0-bi/2,0+bi/2)))+ annotate("text", x = 63, y = -5, label = "3") + ## ThreeToFour: ## circle track geom_path(data=data.frame(x=c(-1*a-(15700:(0)/1000),-1*a),y=c((15.7+bo)-sqrt((15.7)^2-c(15700:(0)/1000,0)^2))),aes(x=x,y=y), colour = "Blue")+ geom_path(data=data.frame(x=c(-1*a-(14590:(0)/1000),-1*a),y=c((15.7+bo)-sqrt((14.59)^2-c(14590:(0)/1000,0)^2))),aes(x=x,y=y))+ geom_path(data=data.frame(x=c(-1*a-(16490:(0)/1000),-1*a),y=c((15.7+bo)-sqrt((16.49)^2-c(16490:(0)/1000,0)^2))),aes(x=x,y=y))+ geom_path(data=data.frame(x=c(-1*a-(16810:(0)/1000),-1*a),y=c((15.7+bo)-sqrt((16.81)^2-c(16810:(0)/1000,0)^2))),aes(x=x,y=y))+ geom_path(data=data.frame(x=c(-1*a-(14910:(0)/1000),-1*a),y=c((15.7+bo)-sqrt((14.91)^2-c(14910:(0)/1000,0)^2))),aes(x=x,y=y))+ annotate("text", x = -31, y = 8, label = "4") + ## straight track geom_path(data=data.frame(x=c(2*a,3*a),y=c(0,0)), colour = "Blue")+ geom_path(data=data.frame(x=c(2*a,3*a,3*a,2*a,2*a),y=c(bo/2,bo/2,-bo/2,-bo/2,bo/2)))+ geom_path(data=data.frame(x=c(2*a,3*a,3*a,2*a,2*a),y=c(0+bi/2,0+bi/2,0-bi/2,0-bi/2,0+bi/2)))+ geom_path(data=data.frame(x=c(c314-a,c314-a),y=c(-bo/2,bo/2)))+ annotate("text", x = c314-a, y = 6, label = "PI") + annotate("text", x = 3*a, y = 6, label = "4") + ## fix aspect ratio to 1:1 coord_fixed()

Oh, and the table corners are rounded 6.35cm (2.5in).
.

by **Cr6** Sun Dec 11, 2016 3:06 am

Sorry not to comment sooner...

Looking really good LTAM. Nice craftsmanship.
Excited to see the "pair" roll together down your set up! Maybe add some colored smoke down the tube at some point to see how it drifts out? Just a thought...sorry to add still another suggestion. I personally know how annoying extra-suggestions can sometimes be when you have completed a real piece of work and then someone stops by at the last minute and says -- "hey looks good but why don't you do this and that to it too?". Smile

The R script looks pretty top notch as well I might add. It is non-trivial IMHO at this point - but I'm just a hack myself.

by **LongtimeAirman** Mon Dec 12, 2016 1:57 am

.
Cr6, Thanks. I should have been clearer. I'll admit to too much psychic stress over the last month. Mostly concerning our country's ongoing train wreck. This project is a positive relief. Craftsmanship? I prefer thrift shops and junk piles. Colored smoke? Oh my.

I'm looking for suggestions on the R code. Criticism is better than compliments. Hack it. What would make you use it?

Nevyn, I don't like coding trash. Please mark errors or make suggestions. Also, you indicated an opportunity to study R. Any insights or lessons learned?

I'm good with constraints. Clearly, R is most suitable for large data groups, which is almost opposite from the Pi=4 setup, or any other Miles R project that comes to my mind. Another R package, ggvis, is supposed to make browser interaction possible. I'll look into it.
.

by **Nevyn** Mon Dec 12, 2016 8:33 pm

Hey Airman, I can't offer too much advice specific to R because I didn't get that far into it but I can offer some suggestions about coding standards. As R is a language for mathematicians rather than programmers, you are going to find a lot of examples of bad coding style. I would even go so far as to say that the language itself promotes it.

Take this line for example:

Code:: geom_path(data=data.frame(x=c(-1*a-(15700:(0)/1000),-1*a),y=c((15.7+bo)-sqrt((15.7)^2-c(15700:(0)/1000,0)^2))),aes(x=x,y=y), colour = "Blue")

It is doing too much and is confusing. You might know what it is doing today but will you understand it in a years time? Make use of variables for clarity. Even just a bit of whitespace can make it so much more readable. For example, even without using variables I would write that line like this:

Code:: geom_path( data=data.frame( x=c( -1*a - ( 15700:(0)/1000 ), -1*a ), y=c( ( 15.7+bo ) - sqrt( (15.7)^2 - c( 15700:(0)/1000, 0 )^2 ) ) ), aes( x=x, y=y ), colour = "Blue" )

Make whitespace your friend. There are no prizes for doing the most in the smallest file size but you will thank yourself later for well formatted code.

You have a few -1*a statements in there which should use the unary operator which is just -a. No need for an expensive multiplication just to make something negative. If you are using it in an expression you can use whitespace to specify exactly what you want, for example: 1--a won't work but 1 - -a will work. You could also do it once and assign it to a variable to save even more computations.

This is using a function called 'c'. Not a good function name. What does it do? There is no way to tell that just from a single letter name. A function name should be descriptive which is why I have called R an ugly language in the past. Since I can't see the function definition in your code I assume it is being pulled in from a library or is a core R function so it may not be your fault but you could still make your own code more readable by assigning the function to a better name.

Turns out 'c' is a core function that concatenates values into an array. See how if they had called it 'concat' it would be self-descriptive.

You should declare your own functions to make things clear. Take this section as an example:

Code:: ## circle track geom_path(data=data.frame(x=c(-1*a+(15700:(0)/1000),-1*a),y=c((15.7+bo)-sqrt((15.7)^2-c(15700:(0)/1000,0)^2))),aes(x=x,y=y), colour = "Blue")+ geom_path(data=data.frame(x=c(-1*a+(14590:(0)/1000),-1*a),y=c((15.7+bo)-sqrt((14.59)^2-c(14590:(0)/1000,0)^2))),aes(x=x,y=y))+ geom_path(data=data.frame(x=c(-1*a+(16490:(0)/1000),-1*a),y=c((15.7+bo)-sqrt((16.49)^2-c(16490:(0)/1000,0)^2))),aes(x=x,y=y))+ geom_path(data=data.frame(x=c(-1*a+(16810:(0)/1000),-1*a),y=c((15.7+bo)-sqrt((16.81)^2-c(16810:(0)/1000,0)^2))),aes(x=x,y=y))+ geom_path(data=data.frame(x=c(-1*a+(14910:(0)/1000),-1*a),y=c((15.7+bo)-sqrt((14.91)^2-c(14910:(0)/1000,0)^2))),aes(x=x,y=y))+

This could be written as a function that takes an array as input. Try something like this:

Code:: // declare a function // I assume a is an angle, not sure what bo is createCircleTrack <- function( a, bo, values, colour ) { n = 0 // not sure what to initialize this too as I don't know what geom_path is returning but it should be the equivalent of zero, not null na = -a // negative a for( i in values ) { // use variables to reduce clutter x = c( na + ( i:(0)/1000), na ) y = c( i/1000 + bo - sqrt( (i/1000)^2-c( i:(0)/1000, 0 )^2 ) n += geom_path( data=data.frame( x=x, y=y ), aes( x=x, y=y ), colour=colour ) // not sure if += operator is supported but it just means n = n+<some value> } return n } // call the function path <- createCircleTrack( a, bo, c( 15700, 14590, 16490, 16810, 14910 ), "Blue" )

Now, you might be thinking that it took more lines of code to do the same thing but it becomes so much easier to fix when you find an error in it and if you call it more than once then you have saved lines of code. It also makes is much easier to copy into another project.

I hope that helps a little bit. Liberal use of whitespace, meaningful variable names and good function use go a long way to creating good, maintainable, re-usable code.

by **Cr6** Tue Dec 13, 2016 1:42 am

There are a few packages for formatting. Nothing fantastic yet but they work:

https://cran.r-project.org/web/packages/formatR/formatR.pdf
library(formatR)

messy <- readLines("C:\\Apache\\PI4.R")
#tidy_source(messy)
## the formatted version
tidy_source(text = messy)

Code:: library(ggplot2) ###################################### ## Pi=4 ## ## Intended to recreate ## Steven Oostdijk's ## Pi=4 experiment as described in ## ###################################### http://milesmathis.com/pi7.pdf ## -------------------------------- ## Posted at ## ###################################### http://milesmathis.forumotion.com/ ## -------------------------------- ## Contributing to a future ## ###################################### Miles Mathis R project ## Input data used: ## 1) The unit circle's diameter ## 2) InsideTrackWidth ###################################### ## 3) OutsideTrackWidth ## 4) Table length and width ## -------------------------------- ## Replace ###################################### with your data to ## plot your own tracks ## -------------------------------- ## measurements in cm ###################################### ## unless noted otherwise ## The tracklengths are scaled to the working diameter CHANGE a_diameter ###################################### HERE a_diameter <- 31.4 a <- a_diameter a_diaInInches <- a_diameter/2.54 a_diaInInches ## [1] 12.3622 ## CHANGE INSIDE AND OUTSIDE DIAMETERS HERE The pvc inside diameter is the trackWidthIn. 5/8' ## converted to centimeters b_trackWidthIn <- 2.54 * (5/8) bi <- b_trackWidthIn ## The pvc outside diameter is the trackWidthOut. 7/8' converted to centimeters b_trackWidthOut <- 2.54 * (7/8) bo <- b_trackWidthOut ## The circle track length, 0-4, is the circular track's centerline circumference c_circumference <- 3.14159 * a_diameter c314 <- c_circumference ## c314=98.6459 The radii needed to plot the circular track: 14.590, 14.910, 15.700, 16.490, 16.810 ## (sorted) r <- a_diameter/2 rOut <- r + bo/2 rIn <- r - bo/2 rOut2 <- r + bi/2 rIn2 <- r - bi/2 ## For rough (unknown ramp) overall length estimate, the total length will be: 1) ramp(a_diameter), ## 2)initNegOneToZero(a_diameter), and 3) straight track length (4*a_diameter). A total rough ## estimate plot length of 6*a_diameter d_straight <- 6 * a_diameter ## d_straight = 188.4 ## CHANGE TABLE DIMENSIONS (T1 and T2) HERE My workspace limit, table dimensions, is 29.5X71.25in. ## Convert to cm. T1 <- 29.5 * 2.54 ## T1 = 74.93 T2 <- 71.25 * 2.54 ## T2 = 180.975 xCoordsInit <- c(-T2/2, -T2/2, T2/2, T2/2, -T2/2) yCoordsInit <- c(-T1/2, T1/2, T1/2, -T1/2, -T1/2) ## With a_diameter=31.4, d_straight = 188.4 > T2 = 180.975. I've exceeded my table length limit by a ## few centimeters. I can gain some centimeters by aligning the straight track to the table's ## diagonal. ## For my special case, to determine a diagonal layout Calculate table rotation MyTable <- cbind(xCoordsInit, yCoordsInit) MyTable ## xCoordsInit yCoordsInit [1,] -90.4875 -37.465 [2,] -90.4875 37.465 [3,] 90.4875 37.465 [4,] 90.4875 ## -37.465 [5,] -90.4875 -37.465 Rotation angle equals neg arcTan((T1/2)/(T2/2)) = neg ## arcTan(37.465/90.4875) Angle <- (-1) * atan(T1/T2) ## Angle in radians Angle ## -0.3925... AngInDeg <- Angle * 360/(2 * 3.14159) AngInDeg ## -22.49deg x'<- x*cos(theta)+ysin(theta) y'<- x*(-1)sin(theta)+ycos(theta) ZRotation <- matrix(c(cos(Angle), sin(Angle), (-1) * sin(Angle), cos(Angle)), nrow = 2, ncol = 2, byrow = TRUE) ZRotation dim(MyTable) TR <- MyTable %*% ZRotation TR ## [,1] [,2] [1,] -97.93679 0.00000 [2,] -69.27286 69.23066 [3,] 97.93679 0.00000 [4,] 69.27286 ## -69.23066 [5,] -97.93679 0.00000 I need a better way to transfer both table contents, (initial and ## final) for the ggplot geom_path function. xCoordsFinal <- c(-97.93678513/2, -69.27286231/2, 97.93678513/2, 69.27286231/2, -97.93678513/2) yCoordsFinal <- c(-0, 69.23066104, 0, -69.23066104, -0) ## plot(xCoordsFinal,yCoordsFinal) The ramp's horiz distance must be under 31.4cm to gain any more ## cm's. It's looking ugly for Oogly. ggplot(data = data.frame(x = 1, y = 1), aes(x, y)) + ggtitle("Pi=4 Track Layout on My Almost Too Small Table\nEach unit length here is 31.4cm (or 12.4in)") + ## tabletop: geom_path(data = data.frame(x = c(-T2/2, -T2/2, T2/2, T2/2, -T2/2), y = c(-T1/2, T1/2, T1/2, -T1/2, -T1/2)), colour = "Red") + geom_path(data = data.frame(x = c(TR[1, 1], TR[2, 1], TR[3, 1], TR[4, 1], TR[5, 1]), y = c(TR[1, 2], TR[2, 2], TR[3, 2], TR[4, 2], TR[5, 2]))) + ## Track Centerlines are blue ramps: circle track geom_path(data = data.frame(x = c(-3 * a, -2 * a), y = c(bo, bo)), colour = "Blue") + geom_path(data = data.frame(x = c(-3 * a, -2 * a, -2 * a, -3 * a, -3 * a), y = c(bo/2, bo/2, 1.5 * bo, 1.5 * bo, bo/2))) + geom_path(data = data.frame(x = c(-3 * a, -2 * a, -2 * a, -3 * a, -3 * a), y = c(bo + bi/2, bo + bi/2, bo - bi/2, bo - bi/2, bo + bi/2))) + ## straight track geom_path(data = data.frame(x = c(-3 * a, -2 * a), y = c(0, 0)), colour = "Blue") + geom_path(data = data.frame(x = c(-3 * a, -2 * a, -2 * a, -3 * a, -3 * a), y = c(bo/2, bo/2, -bo/2, -bo/2, bo/2))) + geom_path(data = data.frame(x = c(-3 * a, -2 * a, -2 * a, -3 * a, -3 * a), y = c(0 + bi/2, 0 + bi/2, 0 - bi/2, 0 - bi/2, 0 + bi/2))) + annotate("text", x = -2.5 * a, y = 8, label = "Ramps") + annotate("text", x = -63, y = -5, label = "-1") + ## NegOneToZero: circle track geom_path(data = data.frame(x = c(-2 * a, -1 * a), y = c(bo, bo)), colour = "Blue") + geom_path(data = data.frame(x = c(-2 * a, -1 * a, -1 * a, -2 * a, -2 * a), y = c(bo/2, bo/2, 1.5 * bo, 1.5 * bo, bo/2))) + geom_path(data = data.frame(x = c(-2 * a, -1 * a, -1 * a, -2 * a, -2 * a), y = c(bo + bi/2, bo + bi/2, bo - bi/2, bo - bi/2, bo + bi/2))) + ## straight track geom_path(data = data.frame(x = c(-2 * a, -1 * a), y = c(0, 0)), colour = "Blue") + geom_path(data = data.frame(x = c(-2 * a, -1 * a, -1 * a, -2 * a, -2 * a), y = c(bo/2, bo/2, -bo/2, -bo/2, bo/2))) + geom_path(data = data.frame(x = c(-2 * a, -1 * a, -1 * a, -2 * a, -2 * a), y = c(0 + bi/2, 0 + bi/2, 0 - bi/2, 0 - bi/2, 0 + bi/2))) + annotate("text", x = -31, y = -5, label = "0") + ## ZeroToOne: circle track geom_path(data = data.frame(x = c(-1 * a + (15700:(0)/1000), -1 * a), y = c((15.7 + bo) - sqrt((15.7)^2 - c(15700:(0)/1000, 0)^2))), aes(x = x, y = y), colour = "Blue") + geom_path(data = data.frame(x = c(-1 * a + (14590:(0)/1000), -1 * a), y = c((15.7 + bo) - sqrt((14.59)^2 - c(14590:(0)/1000, 0)^2))), aes(x = x, y = y)) + geom_path(data = data.frame(x = c(-1 * a + (16490:(0)/1000), -1 * a), y = c((15.7 + bo) - sqrt((16.49)^2 - c(16490:(0)/1000, 0)^2))), aes(x = x, y = y)) + geom_path(data = data.frame(x = c(-1 * a + (16810:(0)/1000), -1 * a), y = c((15.7 + bo) - sqrt((16.81)^2 - c(16810:(0)/1000, 0)^2))), aes(x = x, y = y)) + geom_path(data = data.frame(x = c(-1 * a + (14910:(0)/1000), -1 * a), y = c((15.7 + bo) - sqrt((14.91)^2 - c(14910:(0)/1000, 0)^2))), aes(x = x, y = y)) + geom_path(data = data.frame(x = c(-1 * a + 14.59, -1 * a + 16.81), y = c(15.7 + bo, 15.7 + bo))) + annotate("text", x = -21, y = 18, label = "1") + ## straight track geom_path(data = data.frame(x = c(-1 * a, 0 * a), y = c(0, 0)), colour = "Blue") + geom_path(data = data.frame(x = c(-1 * a, 0 * a, 0 * a, -1 * a, -1 * a), y = c(bo/2, bo/2, -bo/2, -bo/2, bo/2))) + geom_path(data = data.frame(x = c(-1 * a, 0 * a, 0 * a, -1 * a, -1 * a), y = c(0 + bi/2, 0 + bi/2, 0 - bi/2, 0 - bi/2, 0 + bi/2))) + annotate("text", x = 0, y = -5, label = "1") + ## OneToTwo: circle track geom_path(data = data.frame(x = c(-1 * a + (15700:(0)/1000), -1 * a), y = c((15.7 + bo) + sqrt((15.7)^2 - c(15700:(0)/1000, 0)^2))), aes(x = x, y = y), colour = "Blue") + geom_path(data = data.frame(x = c(-1 * a + (14590:(0)/1000), -1 * a), y = c((15.7 + bo) + sqrt((14.59)^2 - c(14590:(0)/1000, 0)^2))), aes(x = x, y = y)) + geom_path(data = data.frame(x = c(-1 * a + (16490:(0)/1000), -1 * a), y = c((15.7 + bo) + sqrt((16.49)^2 - c(16490:(0)/1000, 0)^2))), aes(x = x, y = y)) + geom_path(data = data.frame(x = c(-1 * a + (16810:(0)/1000), -1 * a), y = c((15.7 + bo) + sqrt((16.81)^2 - c(16810:(0)/1000, 0)^2))), aes(x = x, y = y)) + geom_path(data = data.frame(x = c(-1 * a + (14910:(0)/1000), -1 * a), y = c((15.7 + bo) + sqrt((14.91)^2 - c(14910:(0)/1000, 0)^2))), aes(x = x, y = y)) + geom_path(data = data.frame(x = c(-1 * a, -1 * a), y = c(31.4 + bo/2, 2 * 16.81 + bo/2))) + annotate("text", x = -31, y = 29, label = "2") + ## straight track geom_path(data = data.frame(x = c(0, a), y = c(0, 0)), colour = "Blue") + geom_path(data = data.frame(x = c(0, a, a, 0 * a, 0 * a), y = c(bo/2, bo/2, -bo/2, -bo/2, bo/2))) + geom_path(data = data.frame(x = c(0, a, a, 0 * a, 0 * a), y = c(0 + bi/2, 0 + bi/2, 0 - bi/2, 0 - bi/2, 0 + bi/2))) + annotate("text", x = 32, y = -5, label = "2") + ## TwoToThree: circle track geom_path(data = data.frame(x = c(-1 * a - (15700:(0)/1000), -1 * a), y = c((15.7 + bo) + sqrt(15.7^2 - c(15700:(0)/1000, 0)^2))), aes(x = x, y = y), colour = "Blue") + geom_path(data = data.frame(x = c(-1 * a - (14590:(0)/1000), -1 * a), y = c((15.7 + bo) + sqrt((14.59)^2 - c(14590:(0)/1000, 0)^2))), aes(x = x, y = y)) + geom_path(data = data.frame(x = c(-1 * a - (16490:(0)/1000), -1 * a), y = c((15.7 + bo) + sqrt((16.49)^2 - c(16490:(0)/1000, 0)^2))), aes(x = x, y = y)) + geom_path(data = data.frame(x = c(-1 * a - (16810:(0)/1000), -1 * a), y = c((15.7 + bo) + sqrt((16.81)^2 - c(16810:(0)/1000, 0)^2))), aes(x = x, y = y)) + geom_path(data = data.frame(x = c(-1 * a - (14910:(0)/1000), -1 * a), y = c((15.7 + bo) + sqrt((14.91)^2 - c(14910:(0)/1000, 0)^2))), aes(x = x, y = y)) + geom_path(data = data.frame(x = c(-1 * a - 14.59, -1 * a - 16.81), y = c(15.7 + bo, 15.7 + bo))) + annotate("text", x = -42, y = 18, label = "3") + ## straight track geom_path(data = data.frame(x = c(a, 2 * a), y = c(0, 0)), colour = "Blue") + geom_path(data = data.frame(x = c(a, 2 * a, 2 * a, a, a), y = c(bo/2, bo/2, -bo/2, -bo/2, bo/2))) + geom_path(data = data.frame(x = c(a, 2 * a, 2 * a, a, a), y = c(0 + bi/2, 0 + bi/2, 0 - bi/2, 0 - bi/2, 0 + bi/2))) + annotate("text", x = 63, y = -5, label = "3") + ## ThreeToFour: circle track geom_path(data = data.frame(x = c(-1 * a - (15700:(0)/1000), -1 * a), y = c((15.7 + bo) - sqrt((15.7)^2 - c(15700:(0)/1000, 0)^2))), aes(x = x, y = y), colour = "Blue") + geom_path(data = data.frame(x = c(-1 * a - (14590:(0)/1000), -1 * a), y = c((15.7 + bo) - sqrt((14.59)^2 - c(14590:(0)/1000, 0)^2))), aes(x = x, y = y)) + geom_path(data = data.frame(x = c(-1 * a - (16490:(0)/1000), -1 * a), y = c((15.7 + bo) - sqrt((16.49)^2 - c(16490:(0)/1000, 0)^2))), aes(x = x, y = y)) + geom_path(data = data.frame(x = c(-1 * a - (16810:(0)/1000), -1 * a), y = c((15.7 + bo) - sqrt((16.81)^2 - c(16810:(0)/1000, 0)^2))), aes(x = x, y = y)) + geom_path(data = data.frame(x = c(-1 * a - (14910:(0)/1000), -1 * a), y = c((15.7 + bo) - sqrt((14.91)^2 - c(14910:(0)/1000, 0)^2))), aes(x = x, y = y)) + annotate("text", x = -31, y = 8, label = "4") + ## straight track geom_path(data = data.frame(x = c(2 * a, 3 * a), y = c(0, 0)), colour = "Blue") + geom_path(data = data.frame(x = c(2 * a, 3 * a, 3 * a, 2 * a, 2 * a), y = c(bo/2, bo/2, -bo/2, -bo/2, bo/2))) + geom_path(data = data.frame(x = c(2 * a, 3 * a, 3 * a, 2 * a, 2 * a), y = c(0 + bi/2, 0 + bi/2, 0 - bi/2, 0 - bi/2, 0 + bi/2))) + geom_path(data = data.frame(x = c(c314 - a, c314 - a), y = c(-bo/2, bo/2))) + annotate("text", x = c314 - a, y = 6, label = "PI") + annotate("text", x = 3 * a, y = 6, label = "4") + ## fix aspect ratio to 1:1 coord_fixed()

by **LongtimeAirman** Fri Dec 16, 2016 11:11 pm

.
Ready.

We’re looking down at two 7/16in steel ball bearings. Pull down that string on the left. It opens upward a cabinet hinge penetrated by the highest of three pipe clamp u-bolts in the assembly (I reamed the original screw holes open slightly to fit). The string gives the hinge its ‘fixed’ bolt position as it also sits on the next u-bolt just below it. The top u-bolt is rubber banded to a full 5/8x2in bolt and half a clamp (not visible here). As you can see, the bolt holds 4 large and 9 smaller washers that make up the top of an initial raceway. Just below, the ramp openings are at 15cm above the table.

Proof that pi=4 - Page 2 Open10

Gone.

Below you can see things are coming together, in some off center fashion. Speed trials are next. I’ll lay out two long straights and try to determine what my ramp’s vertical as well as horizontal components should be before I make any final track cuts. As I show with the R code plot, the complete layout for my diameter (31.4cm) should fit on the tabletop (please forgive the corner extension) with just a couple of centimeters to spare.

Proof that pi=4 - Page 2 Retria10

We should note that the balls’ paths over the small washer raceway involves curved motion – about 40deg - before a brief freefall. The ramps also force the balls through a 90deg change in direction to get to the tabletop, more curved motion. I’m not at all sure I can calculate the velocity changes complicated as they are by the compound velocities of gravitational acceleration, though I believe Steven O suggested I try. I suspect he used straight inclined ramps with a small final angle change – about 15cm high, ok, but how long? Of course it doesn’t matter what causes the initial velocity since we are only interested in the motion through the marked tracks. Using the quick pair of tracks here (held down with the weight of two wrenches), the steel balls exiting the tubes travel upward to reach a peak suggesting, as we might expect, pi/4 the height of the ready position.

Proof that pi=4 - Page 2 Pieces10

//////////////////////////////////////////////////////////////////////////////////////

Pi = 4 R Code Update.

Thanks for helping. I’ve cleaned, white-spaced and added a variable list to the code. I don’t know how to program with the geom_path function yet, so that must wait. I see that I’ve made short and long variable names, or more, for the same object - the long names are mainly for the reader. The formatR product above is just plain awful; though how would I know?

Code:: library(ggplot2) ################################################ ## ## Pi=4 ## ################################################ ## ## Intended to recreate ## Steven Oostdijk's ## Pi=4 experiment as described in ## http://milesmathis.com/pi7.pdf ## ------------------------------------------ ## Posted at ## http://milesmathis.forumotion.com/ ## ------------------------------------------ ## Contributing to a future ## Miles Mathis R project ## ################################################ ## Input data used: ## 1) The unit circle's diameter ## 2) InsideTrackWidth ## 3) OutsideTrackWidth ## 4) Table length and width ## ------------------------------------------ ## Replace with your data to ## plot your own tracks ## ------------------------------------------ ## measurements in cm ## unless noted otherwise ################################################ ## ## Variables Used: ## ## a, a_diameter, a_diaInInches - The unit diameter ## Angle, AngInDeg - Table rotation aligning horiz straight ## track to the table diagonal ## bi, b_trackWidthIn - Track inside diameter ## bo, b_trackWidthOut - Track outside diameter ## c314, c_circumference - Equals 3.14*a ## r - Equals a_diameter/2 ## rIn - Equals r - b_trackWidthOut/2 ## rIn2 - Equals r - b_trackWidthIn/2 ## rOut - Equals r + b_trackWidthIn/2 ## rOut2 - Equals r + b_trackWidthOut/2 ## straightEst - Equals 6*a, longest straight length ## T1 - Table width ## T2 - Table length ## xCoordsInit - Table x coordinates ## yCoordsInit - Table y coordinates ## MyTable - Matrix of table coordinates ## ZRotation - Matrix used to calculate rotation coordinates ## TR - Matrix multiplication product of MyTable and ZRotation ## xCoordsFinal - Rotated table x coordinates ## yCoordsFinal - Rotated table y coordinates ## ################################################ ## ## The tracklengths are scaled ## to the working diameter ## CHANGE a_diameter HERE a_diameter <- 31.4 a_diameter ##[1] 31.4 ## The varible "a" is used in in place of "a_diameter" in the ## geom_path plot commands in order to reduce the plotting code. a <- a_diameter a ## [1] 31.4 ## show "a_diameter" and "a" in inches. a_diaInInches <- a_diameter/2.54 a_diaInInches ## [1] 12.3622 ############################################# ## ## CHANGE INSIDE AND OUTSIDE TRACK DIAMETERS HERE ## ## b_trackWidthIn is the pvc inside diameter. ## My pvc inside diameter is 5/8", converting to centimeters b_trackWidthIn <- 2.54*(5/8) b_trackWidthIn ## [1] 1.5875 ## "bi" equals "b_trackWidthIn", to simplify the geom_path commands. bi <- b_trackWidthIn bi ## [1] 1.5875 ## b_trackWidthOut is the pvc Outside diameter. Enter and convert 7/8 ## inches into centimeters. b_trackWidthOut <- 2.54*(7/8) b_trackWidthOut ## [1] 2.2225 ## "bo" equals "b_trackWidthOut", again, to simplify the geom_path commands. bo <- b_trackWidthOut bo ## [1] 1.5875 ############################################# ## ## Calculate the pi=3.14 circumference for the working diameter ## The circle track length, 0-4, is the circular ## track's centerline circumference c_circumference <- 3.14159*a_diameter c_circumference ## [1] 98.64593 ## "c314" equals "c_circumference". Used in the geom_path commands. c314 <- c_circumference c314 ## [1] 98.64593 ############################################# ## ## Calculate the the five radii used to plot ## each quadrant of the circular track. ## "r" is the centerline radius, half our working diameter r <- a_diameter/2 r ## [1] 15.7 rIn <- r - b_trackWidthOut/2 rIn ## [1] 14.58875 rIn2 <- r - b_trackWidthIn/2 rIn2 ##[1] 14.90625 rOut <- r + b_trackWidthIn/2 rOut ## [1] 16.81125 rOut2 <- r + b_trackWidthOut/2 rOut2 ## [1] 16.81125 ############################################# ## ## CHANGE TABLE DIMENSIONS (T1 and T2) HERE ## My workspace limit, table dimensions, is 29.5X71.25in. ## Convert to cm. T1 <- 29.5*2.54 T1 ## [1] 74.93 T2 <- 71.25*2.54 T2 ## [1] 180.975 ## The table coordinates: xCoordsInit <- c(-T2/2,-T2/2,T2/2,T2/2,-T2/2) yCoordsInit <- c(-T1/2,T1/2,T1/2,-T1/2,-T1/2) ############################################# ## ## Calculate the rough (unknown ramp) overall length estimate ## ## The total straight length is found by adding the following sections ## (along with their corresponding "a" lengths): 1) ramp(a_diameter); ## 2)initNegOneToZero(a_diameter); and 3) track length (4*a_diameter). ## ## A total rough estimate plot length of 6*a_diameter straightEst <- 6*a_diameter straightEst ## [1] 188.4 ############################################# ## First reality check. ## With a_diameter=31.4, straightEst = 188.4 > T2 = 180.975. ## I've exceeded my table length limit by a few centimeters. ## I can gain some centimeters by aligning the straight ## track to the table's diagonal. ## ## Calculate table rotation ## Table coordinates as a matrix MyTable <- cbind(xCoordsInit,yCoordsInit) MyTable ## xCoordsInit yCoordsInit ##[1,] -90.4875 -37.465 ##[2,] -90.4875 37.465 ##[3,] 90.4875 37.465 ##[4,] 90.4875 -37.465 ##[5,] -90.4875 -37.465 ## Rotation angle equals neg arcTan((T1/2)/(T2/2)) ## = neg arcTan(37.465/90.4875). Angle is in radians. Angle <- -atan(T1/T2) Angle ## [1] -0.3925467 ## Show the angle in degrees AngInDeg <- Angle*360/(2*3.14159) AngInDeg ## [1] -22.49129 ## Build a z-rotation matrix from the rotation identities: ## x'<- x*cos(theta)+ysin(theta) ## y'<- x*(-1)sin(theta)+ycos(theta) ZRotation <- matrix(c(cos(Angle),sin(Angle),(-1)*sin(Angle),cos(Angle)),nrow = 2,ncol = 2,byrow = TRUE) ZRotation ## [,1] [,2] ## [1,] 0.9239378 -0.3825427 ## [2,] 0.3825427 0.9239378 ## Matrix multiply MyTable and ZRotation to find the ## rotated table coordinates "TR". TR <- MyTable%*%ZRotation TR ## [,1] [,2] ##[1,] -97.93679 0.00000 ##[2,] -69.27286 69.23066 ##[3,] 97.93679 0.00000 ##[4,] 69.27286 -69.23066 ##[5,] -97.93679 0.00000 ## Here I'll break TR into separate x and y coordinate strings ## (initial and final) for the ggplot geom_path function. xCoordsFinal <- c(-97.93678513/2,-69.27286231/2,97.93678513/2,69.27286231/2,-97.93678513/2) yCoordsFinal <- c(-0,69.23066104,0,-69.23066104,-0) ## The ramp's horiz distance must be under 31.4cm to ## gain any more cm's. It's looking ugly for Oogly. ############################################# ## ## Plot tracks, table and rotated table ## CHANGE TITLE HERE ggplot( data=data.frame( x=1, y=1 ),aes( x,y ) ) + ggtitle( "Pi=4 Track Layout on My Almost Too Small Table\nEach unit length here is 31.4cm (or 12.4in)" ) + ## Tabletop (shown in red): geom_path( data=data.frame( x=c( -T2/2, -T2/2, T2/2, T2/2, -T2/2), y=c( -T1/2, T1/2, T1/2, -T1/2, -T1/2 ) ), colour = "Red" ) + ## Rotated tabletop: geom_path( data=data.frame( x=c( TR[1,1], TR[2,1], TR[3,1], TR[4,1], TR[5,1]),y=c(TR[1,2], TR[2,2], TR[3,2], TR[4,2], TR[5,2] ) ) ) + ## Plot both tracks in six sections each: ## 1)Ramp; 2)NegOneToZero; 3)ZeroToOne; 4)OneToTwo; 5)TwoToThree: and 4)ThreeToFour. ## Track Centerlines are blue. ## Text annotations are added in their appropriate sections. ## ramps: ## circle track geom_path( data=data.frame( x = c( -3*a, -2*a ), y = c( bo,bo ) ), colour = "Blue" ) + geom_path( data=data.frame( x = c( -3*a, -2*a, -2*a, -3*a, -3*a ), y = c( bo/2, bo/2, 1.5*bo, 1.5*bo, bo/2) ) ) + geom_path( data=data.frame( x = c( -3*a, -2*a, -2*a,-3*a,-3*a ), y = c( bo + bi/2, bo + bi/2, bo - bi/2, bo - bi/2, bo + bi/2) ) ) + ## straight track geom_path( data=data.frame( x = c( -3*a, -2*a ), y = c( 0,0 ) ), colour = "Blue" )+ geom_path( data=data.frame( x = c( -3*a, -2*a, -2*a, -3*a, -3*a ), y = c( bo/2, bo/2, - bo/2, - bo/2, bo/2 ) ) )+ geom_path( data=data.frame( x = c( -3*a, -2*a, -2*a, -3*a, -3*a ), y = c( bi/2, bi/2, - bi/2, - bi/2, bi/2 ) ) ) + annotate( "text", x = -2.5*a, y = 8, label = "Ramps" ) + annotate( "text", x = -63, y = -5, label = "-1" ) + ## NegOneToZero: ## circle track geom_path( data=data.frame( x = c( -2*a, -a ) , y = c( bo, bo ) ), colour = "Blue" )+ geom_path( data=data.frame( x = c( -2*a, -a, -a, -2*a, -2*a ), y = c( bo/2, bo/2, 1.5 * bo, 1.5 * bo, bo/2 ) ) ) + geom_path( data=data.frame( x = c( -2*a, -a, -a, -2*a, -2*a), y = c( bo + bi/2, bo + bi/2, bo - bi/2, bo - bi/2, bo + bi/2 ) ) ) + ## straight track geom_path( data=data.frame( x = c( -2*a, -a ), y = c( 0, 0 ) ), colour = "Blue" ) + geom_path( data=data.frame( x = c( -2*a, -a, -a, -2*a, -2*a), y = c( bo/2, bo/2, -bo/2, -bo/2, bo/2 ) ) ) + geom_path( data=data.frame( x = c( -2*a, -a, -a, -2*a, -2*a), y = c( bi/2, bi/2, -bi/2, -bi/2, bi/2 ) ) ) + annotate( "text", x = -31, y = -5, label = "0") + ## ZeroToOne: ## circle track geom_path( data=data.frame( x = c( - a + ( 15700:(0)/1000 ), - a), y = c( 15.7 + bo - sqrt( ( 15.7)^2 - c( 15700:(0)/1000,0 )^2 ) ) ), aes( x =x, y = y ), colour = "Blue" )+ geom_path( data=data.frame( x = c( - a + ( 14590:(0)/1000 ), - a), y = c( 15.7 + bo - sqrt( ( 14.59)^2 - c( 14590:(0)/1000,0 )^2 ) ) ), aes( x = x, y = y ) ) + geom_path( data=data.frame( x = c( - a + ( 16490:(0)/1000 ), - a), y = c( 15.7 + bo - sqrt( ( 16.49)^2 - c( 16490:(0)/1000,0 )^2 ) ) ), aes( x = x, y = y ) ) + geom_path( data=data.frame( x = c( - a + ( 16810:(0)/1000 ), - a), y = c( 15.7 + bo - sqrt( ( 16.81)^2 - c( 16810:(0)/1000,0 )^2 ) ) ), aes( x = x, y = y ) ) + geom_path( data=data.frame( x = c( - a + ( 14910:(0)/1000 ), - a), y = c( 15.7 + bo - sqrt( ( 14.91)^2 - c( 14910:(0)/1000,0 )^2 ) ) ), aes( x = x, y = y ) ) + geom_path( data=data.frame( x = c( - a + 14.59, - a + 16.81 ), y = c( 15.7 + bo, 15.7 + bo ) ) ) + annotate( "text", x = -21, y = 18, label = "1" ) + ## straight track geom_path( data=data.frame( x = c( -a, 0 ), y = c( 0, 0 ) ), colour = "Blue" ) + geom_path( data=data.frame( x = c( -a, 0, 0, -a, -a ), y = c( bo/2, bo/2, -bo/2, -bo/2, bo/2 ) ) ) + geom_path( data=data.frame( x = c( -a, 0, 0, -a, -a ), y = c( bi/2, bi/2, -bi/2, -bi/2, bi/2 ) ) ) + annotate( "text", x = 0, y = -5, label = "1") + ## OneToTwo: ## circle track geom_path( data=data.frame( x = c( - a + ( 15700:(0)/1000 ), - a ), y = c( 15.7 + bo + sqrt( (15.7)^2 - c( 15700:(0)/1000,0)^2 ) ) ), aes( x = x, y = y ), colour = "Blue" ) + geom_path( data=data.frame( x = c( - a + ( 14590:(0)/1000 ), - a ), y = c( 15.7 + bo + sqrt( (14.59)^2 - c( 14590:(0)/1000,0)^2 ) ) ), aes( x = x, y = y ) ) + geom_path( data=data.frame( x = c( - a + ( 16490:(0)/1000 ), - a ), y = c( 15.7 + bo + sqrt( (16.49)^2 - c( 16490:(0)/1000,0)^2 ) ) ), aes( x = x, y = y ) ) + geom_path( data=data.frame( x = c( - a + ( 16810:(0)/1000 ), - a ), y = c( 15.7 + bo + sqrt( (16.81)^2 - c( 16810:(0)/1000,0)^2 ) ) ), aes( x = x, y = y ) ) + geom_path( data=data.frame( x = c( - a + ( 14910:(0)/1000 ), - a ), y = c( 15.7 + bo + sqrt( (14.91)^2 - c( 14910:(0)/1000,0)^2 ) ) ), aes( x = x, y = y ) ) + geom_path( data=data.frame( x = c( - a, -a ), y = c( 31.4 + bo/2, 2*16.81 + bo/2 ) ) ) + annotate( "text", x = -31, y = 29, label = "2" ) + ## straight track geom_path( data=data.frame( x = c( 0, a ), y = c( 0, 0 ) ), colour = "Blue" ) + geom_path( data=data.frame( x = c( 0, a, a, 0, 0 ), y = c( bo/2, bo/2, -bo/2, -bo/2, bo/2 ) ) ) + geom_path( data=data.frame( x = c( 0, a, a, 0, 0 ), y = c( bi/2, bi/2, -bi/2, -bi/2, bi/2 ) ) ) + annotate( "text", x = 32, y = -5, label = "2" ) + ## TwoToThree: ## circle track geom_path( data=data.frame( x = c( - a - ( 15700:(0)/1000 ), - a ), y = c( 15.7 + bo + sqrt( 15.7^2 - c( 15700:(0)/1000,0)^2 ) ) ), aes( x = x, y = y ), colour = "Blue" ) + geom_path( data=data.frame( x = c( - a - ( 14590:(0)/1000 ), - a ), y = c( 15.7 + bo + sqrt( 14.59^2 - c( 14590:(0)/1000,0)^2 ) ) ), aes( x = x, y = y ) ) + geom_path( data=data.frame( x = c( - a - ( 16490:(0)/1000 ), - a ), y = c( 15.7 + bo + sqrt( 16.49^2 - c( 16490:(0)/1000,0)^2 ) ) ), aes( x = x, y = y ) ) + geom_path( data=data.frame( x = c( - a - ( 16810:(0)/1000 ), - a ), y = c( 15.7 + bo + sqrt( 16.81^2 - c( 16810:(0)/1000,0)^2 ) ) ), aes( x = x, y = y ) ) + geom_path( data=data.frame( x = c( - a - ( 14910:(0)/1000 ), - a ), y = c( 15.7 + bo + sqrt( 14.91^2 -c( 14910:(0)/1000,0)^2 ) ) ), aes( x = x, y = y ) ) + geom_path( data=data.frame( x = c( - a - 14.59, - a - 16.81), y = c( 15.7 + bo, 15.7 + bo ) ) ) + annotate( "text", x = -42, y = 18, label = "3" ) + ## straight track geom_path( data=data.frame( x = c( a, 2*a ), y = c( 0, 0 ) ), colour = "Blue" ) + geom_path( data=data.frame( x = c( a, 2*a, 2*a, a, a ), y = c( bo/2, bo/2, -bo/2, -bo/2, bo/2 ) ) ) + geom_path( data=data.frame( x = c( a, 2*a, 2*a, a, a ), y = c( bi/2, bi/2, -bi/2, -bi/2, bi/2 ) ) ) + annotate( "text", x = 63, y = -5, label = "3" ) + ## ThreeToFour: ## circle track geom_path( data=data.frame( x = c( - a - ( 15700:(0)/1000 ), - a ), y = c( 15.7 + bo - sqrt( 15.7^2 -c( 15700:(0)/1000,0)^2 ) ) ), aes( x = x, y = y ), colour = "Blue" ) + geom_path( data=data.frame( x = c( - a - ( 14590:(0)/1000 ), - a ), y = c( 15.7 + bo - sqrt( 14.59^2 -c( 14590:(0)/1000,0)^2 ) ) ), aes( x = x, y = y ) ) + geom_path( data=data.frame( x = c( - a - ( 16490:(0)/1000 ), - a ), y = c( 15.7 + bo - sqrt( 16.49^2 -c( 16490:(0)/1000,0)^2 ) ) ), aes( x = x, y = y ) ) + geom_path( data=data.frame( x = c( - a - ( 16810:(0)/1000 ), - a ), y = c( 15.7 + bo - sqrt( 16.81^2 -c( 16810:(0)/1000,0)^2 ) ) ), aes( x = x, y = y ) ) + geom_path( data=data.frame( x = c( - a - ( 14910:(0)/1000 ), - a ), y = c( 15.7 + bo - sqrt( 14.91^2 -c( 14910:(0)/1000,0)^2 ) ) ), aes( x = x, y = y ) ) + annotate( "text", x = -31, y = 8, label = "4" ) + ## straight track geom_path( data=data.frame( x = c( 2*a, 3*a ),y = c( 0, 0 ) ), colour = "Blue" ) + geom_path( data=data.frame( x = c( 2*a, 3*a, 3*a, 2*a, 2*a ), y = c( bo/2, bo/2, -bo/2, -bo/2, bo/2 ) ) ) + geom_path( data=data.frame( x = c( 2*a, 3*a, 3*a, 2*a, 2*a ), y = c( bi/2, bi/2, -bi/2, -bi/2, bi/2 ) ) ) + geom_path( data=data.frame( x = c( c314 - a, c314 - a ), y = c( -bo/2, bo/2 ) ) ) + annotate( "text", x = c314-a, y = 6, label = "PI" ) + annotate( "text", x = 3*a, y = 6, label = "4" ) + ## fix aspect ratio to 1:1 coord_fixed()

.

by **LongtimeAirman** Thu Dec 22, 2016 10:49 pm

.

Pvc tubes held by pvc tape onto a pvc table. *

Milestone update. My first complete track layout, marked with 31.4cm diameter units on both the table (taped surface) as well as the track tubes. The video - not ready for prime time - shows a 10cm out-of-synch difference reaching the 4 mark, with the circle track ball winning.

I removed the table’s circular track drawing and marks before this photo because of the unmatched confusion with the actual track. My ramp is as long as my current setup allows, placing my tube ends 21cm above the table. As such the ramps are too snug, and both tracks as well, having pushed past their table marks overnight despite plenty of tape. I’ll shorten the ramps another cm or so.

Proof that pi=4 - Page 2 Trackl11

Here we see an actual working diameter - in the way. This circle track is too tear shaped to be acceptable – the tubes are most rigid at curvature ends. The zero and four marks cannot meet face-to-face, and so an accurate circle is physically impossible. Next time I’ll lose the container and let the circular track overlap (spiral in).

I’ve been very cautious, gently working suspended tracks with ropes and rags to straighten and mark them. Any unnecessary changes in direction reduces rolling efficiency. Taped (or fixed) track beside untaped positions can form areas of tension and compression resulting in unanticipated bends.

Proof that pi=4 - Page 2 Trackl12

Many unanticipated bends. I must improve my methodology. The circle is trying to lift off the table. Here we can see the straight track 4 mark being pulled up off the table surface while the track tries to snake behind it.

Switching to the more flexible, completely transparent pvc is easily done at this point. I was disappointed when I saw the transparent pvc deformed and even folded, over-packed onto spools at alternate local hardware stores, while the adjacent braided pvc tubes clearly kept their circular cross sections. The stronger braided pvc allow us to view the steel balls positions’, though at some loss in visibility. The braids can serve as surface coordinates - nice perpendicular and parallel guidelines.

Still in progress.

*Polyvinyl chloride

by **LongtimeAirman** Fri Dec 30, 2016 10:56 pm

.
Plenty of practice, but no joy.

My straight track is slightly slower than the circular. Both starting velocities are about 137 cm/s. Using braided pvc, the ball bearings aren’t always visible even in daylight. I’ve also cut a set of clear pvc tracks which I’ve hung up to straighten before final marking and cuts.

Proof that pi=4 - Page 2 Pi4fou10

.

by Ciaolo Sat Dec 31, 2016 5:03 am

Are you sure it's a circular path? It seems slightly oval to me. Is there a way to check and correct it?

by **LongtimeAirman** Sat Dec 31, 2016 12:56 pm

.

Ciaolo wrote:Are you sure it's a circular path? It seems slightly oval to me. Is there a way to check and correct it?

Hi Ciaolo, Thanks for the observation. In my 22Dec post above I include this comment -

This circle track is too tear shaped to be acceptable – the tubes are most rigid at curvature ends. The zero and four marks cannot meet face-to-face, and so an accurate circle is physically impossible. Next time I’ll lose the container and let the circular track overlap (spiral in).

In my latest image you can see a container, my working diameter, in the bottom left corner positioned to catch balls leaving the straight track. I actually use the container as working diameter/circumference to secure my circular track's 0,1, 2 and 3 marks to the table. I allow the circle's end, the four mark, to lift off the table, above the zero mark. I then remove the container and secure the 4 mark onto the table's surface as close to the zero mark as the track allows, thereby 'spiraling-in' to the 4 mark; the circular track is no longer a circle. You may have noticed that Steven's circular track is also slightly deformed. How does one correct for that?

Curved motion works with spirals and ovals as well as with circles. I could make the entire circular track a spiral. I would plot the spiral image onto the tabletop and lay the track onto it, but then I wouldn't be able to use my 'working diameter' container.

Any ideas?
.

by Ciaolo Sat Dec 31, 2016 1:25 pm

Actually I have an idea: use half a circumference instead of the whole one. This not only removes the problems in creating a perfect shape, but also allows you to measure the final speed.

Cheers

by **LongtimeAirman** Sat Dec 31, 2016 3:18 pm

.
Ciaolo, I like your idea. I look forward to it.

It'll just take me a while as I've committed myself to recreating Steven's demonstration first. I hope I'm not testing everyone's patience.
.

by **Cr6** Sat Dec 31, 2016 7:59 pm

LongtimeAirman wrote:.
Plenty of practice, but no joy.

My straight track is slightly slower than the circular. Both starting velocities are about 137 cm/s. Using braided pvc, the ball bearings aren’t always visible even in daylight. I’ve also cut a set of clear pvc tracks which I’ve hung up to straighten before final marking and cuts.
.

Is the straight tube track pvc too corrugated or uneven which would then impact the ball enough to slow it down slightly? Basically, is it a non-flat rolling surface inside the pvc tube.

by **LongtimeAirman** Sat Dec 31, 2016 11:32 pm

.
Cr6, Correct. The problem is an uneven internal surface within the straight track caused by the coiling tendency.

I've purchased pvc conduit in coils of under a foot diameter, 10 feet long. Pvc sold by the foot off of 100 foot coils is not as pretty in maintaining a circular cross section. The tracks must be straightened sufficiently so that they can be properly measured. The exception - braided pvc allows someone to cut accurate lengths without straightening by using the braids as a measure.

Ok. Two tracks cut to length. One naturally lays the track beginning with the ramp, curved side downward - i.e. the track would coil in the vertical plane. With the circular track one might include a 90deg twist between the ramp and the track in order to ensure that the circular track's coil tendency would remain horizontal on the table surface. The circular track is therefore able to maintain a constant table pressure and cross section.

Laying the straight track is the problem. After the ramp, it also wants to coil back into the vertical plane. As one secures points along the track, the linear areas between the secured points do not maintain a constant pressure with the table. The ball's path, the bottom of the pvc's internal cross section varies between too flat (and wide) and narrow (tall). The ball in the straight track thus has both vertical and horizontal changes that slow it down. The straight track should, eventually, lose its coil, but that may take weeks or months.

It may be easier to lay the straight track such that the coil would remain in the horizontal plane. I believe I would also need a wall board alongside the straight path to secure it too and maintain a straight path direction.

That’s the way it looks to me. The clear pvc is softer and may not spring back into the coil so easily. I should find out.
.

by LloydK Sun Jan 01, 2017 6:44 pm

LongtimeAirman wrote:.
Ciaolo, I like your idea. I look forward to it.

It'll just take me a while as I've committed myself to recreating Steven's demonstration first. I hope I'm not testing everyone's patience.

You're a scientist. Testing things is what scientists do.

by LloydK Sun Jan 01, 2017 6:47 pm

By the way, how hard would it be to make a magnetic levitation tube to reduce friction? Or what about replacing the ball with dry ice?

by kug Tue Oct 23, 2018 4:29 am

Proof of period, "pi" is 4 not 3.14, for circular rotation.

Defined:
x axis is the horizontal direction
y axis is the vertical direction
Radius is 1 meter.
Magnitude of velocity (v) is 1 m/s
Initial point is A at ( 1,0 )
Equation of circle: x^2 + y^2 = 1
Velocity vector is V = - v sin theta X + v cos theta Y
Where X and Y are the orthogonal velocity components
So Vx is - v sin theta
and Vy is v cos theta.

theta is an angle where:
sin theta is y/1
cos theta is x/1

The magnitude of velocity is (v^2 sin^2 theta + v^2 cos^2 theta)^(1/2) = 1
Time traveled is calculated by the distance traveled over the velocity.

The path is A -> B -> C -> D.
Focusing on AB:
Here we project the path onto the y axis and sum the accumulated time to reach B from A.
If we set the number of division in theta to be very large, say 1000.
Velocity can be calculated at a theta position.
dy/dt = cos theta dtheta/dt = cos theta

The time it takes to travel the incremental distance traveled, Vy * dtheta/dt = cos theta * 1/1000,
over velocity at the theta value , Vy = cos theta,
which is ( cos theta * 1/1000 ) / cos theta = 1/1000 sec
The total time to travel from AB is 1 sec.

Correspondingly BC, CD, and DA is also 1 sec. The total is then 4 sec.

by **LongtimeAirman** Tue Oct 23, 2018 1:14 pm

Hi kug. Welcome, thanks for posting. I’m no expert but I can usually work up a critical review for friends.

Proof of period, "pi" is 4 not 3.14, for circular rotation.

Sorry, the title is confusing, suspect and wrong – at least as far as I can tell. A ‘Period’ is a rate of time. A period of “pi” implies the time it takes to travel about the circle. All well and good, but the ‘rate’ interpretation is contradicted by the next sentence fragment “"pi" is 4 not 3.14”.

I must point out that the “"pi" is 4 not 3.14” comparison normally applies to the distance of the circle’s circumference and not the time it takes to travel round the circle. I would agree that Steven Oostdijk proved pi = 4 by demonstrating that the time it took for the balls to travel either of the two paths: a straight line distance of four; and a circle circumference of radius one; are both the same. I think I understand your logic.

Back to the title, the final sentence fragment is just wrong. The proof concerns circular ‘motion’ and not circular ‘rotation’. I'll assume you meant 'motion' and quote part of soostdijk‘s comment earlier in this thread - It's appropriate since you seem to be pulling a "velocity" around a circle. Re: Proof that pi=4. https://milesmathis.forumotion.com/t226p25-proof-that-pi4#1747.

1. Pulling a "velocity" around a circle is not the same as pulling a solid ruler around a circle. The velocity vector will need to be rotated along the path otherwise it would not follow the path. This rotation takes time. So it would not be logical that the length of a circular path measured with a velocity would be the same as measured with a ruler. For all these people shouting that Pi will always remain 3.14, sure, but only for geometric ratios.

Please don't take any of my criticism personally, but you must admit, it may be unreasonable of you to expect positive responses given the problems with the title alone. In my experience, Miles has been quick to reply to questions, although he might also think twice before replying to your effort here. There's too much inaccuracy to give an easy reply.
.

by **Cr6** Thu Oct 25, 2018 1:31 am

Well guys... the only thing about this Mathis paper that keeps me laughing is when does a real rolling ball ever actually reach "3.14xxxxxxxxxxx.....infinity" in the real world? If there was no actual t involved I suppose it could actually go on "forever". Suspect

by kug Fri Oct 26, 2018 11:09 pm

This is the corrected version. The important concept is the 2nd picture.

Proof that pi=4 - Page 2 Bhi3cS1

Proof of period, "pi" is 4 not 3.14, for circular rotation.

Defined:
x axis is the horizontal direction
y axis is the vertical direction
Radius is 1 meter.
Magnitude of velocity (v) is 1 m/s
Initial point is A at ( 1,0 )
Equation of circle: x^2 + y^2 = 1
Position vector is D = r cos theta X + r sin theta Y
Velocity vector is V = - v sin theta X + v cos theta Y
Where X and Y are the orthogonal velocity components
So Vx is - v sin theta
and Vy is v cos theta.

theta is an angle where:
sin theta is y/1
cos theta is x/1

The magnitude of velocity is (v^2 sin^2 theta + v^2 cos^2 theta)^(1/2) = 1
Time traveled is calculated by the distance traveled over the velocity.

The path is A -> B -> C -> D.
Focusing on AB:
Here we project the path onto the y axis and sum the accumulated time to reach B from A.

At t = 0: x = 1, y = 0
theta = 0, cos theta = 1
dx/dt = 0, dy/dt = v = 1 m/s
cos theta dtheta/dt = dy/dt
dtheta/dt = v = 1 m/s

At x = 0, y = 1
t is unknown
theta = pi/2, sin theta = 1
dx/dt = -v = -1 m/s, dy/dt = 0
-sin theta dtheta/dt = dx/dt
dtheta/dt = v = 1 m/s
dtheta/dt always proportional to the velocity

Proof that pi=4 - Page 2 D4Jc19C

Velocity vector equation, V, does not represent the direction of the object, it represents to summation of the velocity vector before and after a point. When theta_r is very small, V is the sum of two vectors of equal magnitude.
v_real = 1/2 V
so dtheta/dt = 1/2 m/s

If we set the number of division in theta to be very large, say 1000.
Theta change from A -> B is 90 degrees, pi/2.
dy/dt = cos theta dtheta/dt = cos theta/2

If theta has 1000 divisions, then t also has 1000 divisions.
Incremental distance traveled, Vy * dt / div = cos theta * 1/1000.
Note V is used because it is the sum of all vectors at a point.
Velocity traveled: dy/dt = cos theta/2.
Time is then calculated:
Time = ( cos theta * 1/1000 ) / (cos theta/2) = 2 / 1000 sec

The total time to travel from AB is 2 sec.
The total distance traveled is sum of magnitude of vector * dt * # of divisions.
Distance traveled in y direction = 1

For a full orbit, A -> B -> C -> D > A:
Total distance is 1*4 = 4 m.
Time taken is 2*4 = 8 sec.

Period of a full circle = 2 pi
2 pi = 8
pi = 4

by kug Fri Oct 26, 2018 11:37 pm

Hi LongtimeAirman, I found about Mathis a week ago and a your forum a couple days ago. The pi = 4 problem seems simple to prove, so this is my attempt.

For example in a front wheel drive vehicle, the forward half of the vehicle is directed of the front wheels. The back half of the vehicle is directed by the rear wheel, which is fixed to the direction of the car.
If the car is driving 100 mph, the magnitude of the vector of the front and back cannot be both 100 mph. They have to be summed up together to be 100 mph in magnitude. Thus the front and back vector of the car is 50 mph.
When the car is turning, the front vector with a magnitude of 50 mph is shifted away from the center. This creates a new direction and a new magnitude that is less than 100 mph.
One interesting thing is if the front wheel is turned, there is also a vector normal to the direction of the vehicle. If the angle is high enough, there is a force limit that overcomes the static force and the vehicle begins to slide. Like in physics, where they slide a block down an angle.
Now that there are three vectors, the rear vector is always in the direction of the vehicle at the previous time. When the third vector is in play, the vehicle to us seems like it is out of control, because it is not responding as we are accustomed with two vectors.

by **LongtimeAirman** Sat Oct 27, 2018 2:12 pm

.
Thanks for the additional background kug. In less than a week after finding out about Miles Mathis you can show us a simple proof of “pi” = 4. It's true, one need only adopt the Manhattan metric* in order to show that pi=4. The metric can be used to explain the cycloid **. The Manhattan metric is used when the tangent line to the circle is replaced with the orthogonal components making up that tangent line. Please see *353a and **353b.

I think it's commendable to jump into the Pi fight, although you may not have been aware of it. Pi = 4 is a point of great contention. My own posting experience began by coming out in defense of pi=4. In that light, your use of ‘circular rotation’ sounded like sarcasm. Circular rotation has a tangential velocity while circular motion is an acceleration comprised of orthogonal velocity components. Your inclusion of an additional diagram showing the tangential velocity vector as comprised of two non-orthogonal velocities makes me doubt you’ve got the metric completely figured out. Sliding vehicles on a racetrack involves curved motion, and not rotation.

If you haven't done so already, please read a few of Miles’ other papers on pi before jumping to any more conclusions. Here's Miles' pi list.

//////\\\\\///////////\\\\\/////

THE GREATEST STANDING ERRORS IN PHYSICS AND MATHEMATICS
http://milesmathis.com/

85. A Clarification of the Equation a=v2/r. I import new information from my π papers to extend my findings regarding orbits. I also show that the centripetal acceleration is not instantaneous. 6pp. http://milesmathis.com/avr2.html

350. What is π? Here I show that π is a centripetal acceleration and that the circumference of any circle has complex dimensions. 6pp. http://milesmathis.com/pi.html

351. The Extinction of π. Here I show that the true value of π, defined as the ratio of circumference to diameter, is 4. 15pp.
http://milesmathis.com/pi2.html

352. Proof from NASA that π is 4. Simple proof from Explorer that overturns π. 5pp.
http://milesmathis.com/pi4.html

353a. The Manhattan Metric. Where I show the specific links to Hilbert's math, further supporting my contention that π=4 in kinematic situations. 11pp. http://milesmathis.com/manh.pdf

353b. The Cycloid and the Kinematic Circumference. I use the cycloid again to explain very briefly why pi=4 when you have motion around a circle. 12pp. http://milesmathis.com/cycloid.pdf

353c. More on the Running Track. This is to clarify my recent addendum to my paper on pi=4. I show that both the distances and velocities are being miscalculated in the curves on normal running tracks. 6pp. http://milesmathis.com/track.pdf
.

by **Jared Magneson** Wed Oct 31, 2018 11:56 pm

Hi Kug, and welcome to the forum!

I too think it's awesome and commendable that you're jumping into things feet-first. So again, as LongtimeAirman stated, don't take it too personally if you're very critical. It's the best and even only way to keep ourselves honest and accurate, at the same time!

Good stuff here though. I like your second presentation.

by kug Thu Nov 01, 2018 11:25 pm

Hi Jared, thanks for the welcome.

I won't take the criticism too personally, I'm figuring out along the way to to illustrate the problem and then solve it mathematically with a realistic example.

I was trying to show how the velocity vector equation is calculating the direction and magnitude at a point. The correct velocity vector equation to use for summing vectors is actually 1/2 of the magnitude velocity vector equation. Inadvertently, I found out acceleration is equal to v^2/2R.

Proof that pi=4 - Page 2 0VRAa6U

Fig 1. Velocity vector equation as is.

Proof that pi=4 - Page 2 8CkAh2U

Fig 2. Shift left of velocity vector equation by 1/2 unit, where 1 unit is 7.5 degrees.

Velocity vector equation:
V = - v sin theta X + v cos theta Y

The angle from A to C is 15 degrees and the angle from A to B is 7.5 degrees. The orange vector is first velocity vector and the green is the second velocity vector. Orange and green vectors are the same size, just rotated due to acceleration vector (small vector colored in brown). The red vector is the orange or green vector added to the acceleration vector.

The fundamental problem is that we assume the starting position A is at rest, ie: v_0 = 0, before we even set t = 0. You need to have momentum to arrive a point A. You don't just appear with a velocity, and then start moving. However, that is exactly what the velocity vector equation does.
Halving the velocity vector equation solves this problem by splitting the vector into two and also doubles the number of divisions. This split separates the preceding and succeeding vectors, and allows the sum of the vectors at any point be equal to the magnitude of V.

If Fig 1. at point B, there are two vectors, AB and BC. The sum of both would be AC which is nearly double of both the orange and green.
If Fig 2. If the velocity vector equation did not put the first vector at point A, but instead put the middle of the first vector at point A, I can show how a = v^2/2R.

The orange and green vectors are the same as in Fig 1, only the initial configuration is different. Notice how much of an acceleration vector is needed to keep the path onto the circular path. In Fig 1, the acceleration vector need to correct a full orange vector distance. But in Fig 2, the amount of acceleration vector needed is only half the orange vector distance.

Derivation of acceleration value in Cartesian coordinates:
similar to http://milesmathis.com/avr3.pdf where it is derived in r and theta.
R is the radius

x^2 + y^2 = R^2
y = sqrt(R-x^2)
dy/dt = 1/2 (R-x^2)^(-.5) *(-2x) dx/dt
= -1/2y * 2x ds/dt
= x/y dx/dt

dx/dt = -y/x dy/dt

Velocity magnitude is constant, C

(dy/dt)^2 + (dx/dt)^2 = C^2
(dy/dt)^2 + (y/x)^2 (dy/dt)^2 = C^2
(1+ y^2/x^2) (dy/dt)^2 = C^2
(x^2 + y^2)/x^2 (dy/dt)^2 = C^2
R^2/x^2 (dy/dt)^2 = C^2
dy/dt = C/R x
dx/dt = - C/R y

Acceleration magnitude is constant ,C1
(d2y/dt2)^2 + (d2x/dt2)^2 = C1^2
d2y/dt2 = (C/R) dx/dt = -(C/R)^2 y
d2x/dt2 = -(C/R) dy/dt = -(C/R)^2 x
(C/R)^4 x^2 + (C/R)^4 y^2 = C1^2
(C/R)^4 (x^2 + y^2) = C1^2
(C/R)^4 R^2 = C1^2
C1 = C^2/R

With the acceleration vector cut by 2:
a = v^2/(2 R)

by **Nevyn** Fri Nov 02, 2018 1:11 am

Unfortunately, Fig 2 is completely invalid. You can not just slide the velocity vector along like that. It is illegal and not physical because it does not adhere to the definition of a velocity.

A velocity is not a thing in its own right. It does not exist, as say a table exists, but is a property of something that does exist. You can say 'That car has a velocity', but you can't say 'That velocity has a car'. Further more, a velocity is a relative property. It is always relative to the current position of that which it belongs to. A velocity is also a future event. The velocity you have now dictates where you will end up.

In the case of circular motion, we are looking at a point on the circumference of a circle. You can choose any point you like, it is completely arbitrary and will not change the results. Whatever point you do choose, though, is where your velocity vector is based. That is the point that represents now and the velocity points from that position to show where it will cause that point to go.

That is why you can't just base that vector somewhere else. It belongs to that point because it is relative to that point. A velocity is the motion, over some set time period, of some thing from one position to another.

by **Jared Magneson** Thu Nov 08, 2018 5:22 am

And this is why you're so critical here, Nevyn. I hate to put that stress on your shoulders, but there it is. Bear it however you must. I didn't take the time to dig through the math here, since I was already convinced of the premise from all the other directions. Good lookin' out, Nevyn.

Don't be discouraged, Kug. Just keep pluggin' away, and take these criticisms for what they are. We NEED to be accurate on these topics, and plug in any holes or perceived weaknesses by beating each other up a bit. Nevyn has helped me personally on many projects, especially stacked spins, and please take his analysis under heavy consideration.

by Sponsored content