Possible Charged Particle Field
4 posters
Page 1 of 15
Page 1 of 15 • 1, 2, 3 ... 8 ... 15 
 Possible Charged Particle Field
Possible Charged Particle Field
.
I believe I’ve found an excellent threejs program for conversion to the charge field. webgl_gpgpu_protoplanet - https://threejs.org/examples/#webgl_gpgpu_protoplanet.

The image shows that the program uses some sort of a particle system. When particles collide, they join, all coalescing into a protoplanet. Controls, with physics parameters is included.
I would like to reprogram the particles with charge and collisions - a charged particle field would make a great simulation/animation. I’ll be happy to do the majority of the work; if anyone else is interested, a team would be ideal. I’ll probably need some help before it’s done. Is this agreeable to everyone?
Nevyn, do you think this is doable? Are the protoplanet's particles robust enough to add spin and charge? Do you see any problem with this approach, teamwork possibility or simply managing this? It is my sincerest wish to end up with something you would be happy to own; otherwise I'd prefer not to waste our time again.
.
I believe I’ve found an excellent threejs program for conversion to the charge field. webgl_gpgpu_protoplanet - https://threejs.org/examples/#webgl_gpgpu_protoplanet.

The image shows that the program uses some sort of a particle system. When particles collide, they join, all coalescing into a protoplanet. Controls, with physics parameters is included.
I would like to reprogram the particles with charge and collisions - a charged particle field would make a great simulation/animation. I’ll be happy to do the majority of the work; if anyone else is interested, a team would be ideal. I’ll probably need some help before it’s done. Is this agreeable to everyone?
Nevyn, do you think this is doable? Are the protoplanet's particles robust enough to add spin and charge? Do you see any problem with this approach, teamwork possibility or simply managing this? It is my sincerest wish to end up with something you would be happy to own; otherwise I'd prefer not to waste our time again.
.
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
It is more aimed at gravity than charge. You could change it to reflect charge interactions, but all of the work will be in the shaders, so you will need to learn GLSL (OpenGL Shader Language), which is pretty much a variant of C. The problem with developing shaders is that you don't have any sort of debugging framework. You just have to change the code, run it, and see what happens. If it doesn't do what you want, then you just have to figure out where the code is wrong. You don't get to write debug statements to a console to tell you what is happening in your code as it runs. It can be extremely frustrating until you get a feel for the way shaders work and what you can do inside of them.
I think it would be beneficial to come up with a project outline. What is the aim of the project? What is it trying to achieve? What do you want it to show? Very broad ideas of what you want it to be. With that, it will be easier to see what is the best way to accomplish those goals.
It doesn't have to be pages of documentation. A lot of my own projects just start out with the goal of learning something. If I want to learn how to develop 3D systems, then I find some interesting problem to implement in a 3D system and keep going until I have something that works, or I have learnt enough, or I just get sick of it. Another project might start with the goal of being able to easily build molecules. As I think over what I want it to look and act like, I see different ways of accomplishing that. I may change my mind on how it operates or what it looks like as I go along. MBL is not what I set out to achieve, but along the way I saw that it was the best way to go and I am really happy that I did. If I had stuck to my original ideas then it would not even be operable yet. At least, no where near what it is capable of now.
I don't want to discourage you. This example could certainly be a good starting point for something. I can help along the way, which that project guide also helps with as it gives me an idea of what you are doing. At this point, I don't have a good picture of what this app will do. See if you can paint me a better picture.
I think it would be beneficial to come up with a project outline. What is the aim of the project? What is it trying to achieve? What do you want it to show? Very broad ideas of what you want it to be. With that, it will be easier to see what is the best way to accomplish those goals.
It doesn't have to be pages of documentation. A lot of my own projects just start out with the goal of learning something. If I want to learn how to develop 3D systems, then I find some interesting problem to implement in a 3D system and keep going until I have something that works, or I have learnt enough, or I just get sick of it. Another project might start with the goal of being able to easily build molecules. As I think over what I want it to look and act like, I see different ways of accomplishing that. I may change my mind on how it operates or what it looks like as I go along. MBL is not what I set out to achieve, but along the way I saw that it was the best way to go and I am really happy that I did. If I had stuck to my original ideas then it would not even be operable yet. At least, no where near what it is capable of now.
I don't want to discourage you. This example could certainly be a good starting point for something. I can help along the way, which that project guide also helps with as it gives me an idea of what you are doing. At this point, I don't have a good picture of what this app will do. See if you can paint me a better picture.
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
After a bit more thought, I'm starting to see some possibilities. I've had a project in the back of my mind for some time and this might be a good way to bring it to life. Essentially it is a charged particle interaction model. Protons and electrons, maybe neutrons, and some rules to govern their behavior based on charge. I have never started this project because I couldn't see how to model the charge field of a particle in an efficient manner.
I think I have found a way. I'm working on some math to calculate the effective charge vector of a particle at some point. It takes into account how far away the point is and how close it is to the poles or equator. The charge field sets the length of the vector and the position of the point determines the direction. The vector is always a repulsion, never an attraction. It can be zero length, but it will always point away from the charged particle. I have an outline for the algorithm, but I haven't coded it and tested it yet.
Does that fit in with what you had in mind? I wasn't sure if you were thinking of charge photon interactions or of larger particles.
I think I have found a way. I'm working on some math to calculate the effective charge vector of a particle at some point. It takes into account how far away the point is and how close it is to the poles or equator. The charge field sets the length of the vector and the position of the point determines the direction. The vector is always a repulsion, never an attraction. It can be zero length, but it will always point away from the charged particle. I have an outline for the algorithm, but I haven't coded it and tested it yet.
Does that fit in with what you had in mind? I wasn't sure if you were thinking of charge photon interactions or of larger particles.
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
.
Yes, the particles are larger, recycling particles. I'm glad you're seeing some possibilities as well as the difficulties. I'm psyched.
This program contains three strong pluses: a particle engine, a control panel, and an orbital/interactive camera. I’d failed to mention the orbital camera previously. The fact that they all work together after so many of my own previous difficulties makes this program especially noteworthy.
The proto-planet program seems to meet the basic requirements of a mainstream planetary formation model. All particulate matter within a distributed gravitational field of a so-called proto-planet is described by each particle’s: radius, density, gravity, position and velocity.
I don’t know how gravity is handled by the program just yet – it doesn’t look complicated. The controls include a dynamic variable, which you can change as the program is running – gravityConstant. The single value seems to be applied equally to all particles and aggregate particles at the same time. Increased gravity increases particle accelerations, velocities and mergers. Decreased gravity slows things down greatly, too slow and most particles won’t merge. Acceleration is a change in the particle’s velocity in reaction to the field it encounters – such as large nearby particles; all accelerations are currently due to gravity only.
We must add the charge field. This involves two changes to the parameter list.
The Goal. Changing the particle parameter list to include charge repulsion and spin.
First, in accordance with the charge field, as long as we know a particle’s radius, we know its gravity. Gravity increases as the inverse – or inverse squared – distance between particles. If gravity is treated as a field in the program’s calculations then we must compound the acceleration calculation by adding repulsive charge to the same calculation. Note that charge repulsion is not as simple as gravity, since particle emission is a function of a charged particle’s latitude – most repulsion is felt over the equator, and the least repulsion is felt approaching a particle’s pole.
Second. We must include each particle’s spin - the tangential velocity at the particle’s equator. Spin is thus both a position and a velocity. There are alternative possibilities in implementing spin, the best scheme I’ve come up with is monitoring the particles two pole positions – north and south, (with the particle’s position directly in-between). The two poles would then define the particles’ spin-axis. Once again, we need the spin axis of each particle to determine how much charge repulsion each particle feels.
I'll need to study the program first, but that’s my suggested game plan. If we get to the first goal, we’ll discuss further plans then. I think the essentials will be in place. The proto particles will continue to merge, but I believe the observed behavior of the particle field will change greatly. The major drawback is the fact that adding spin adds a great deal more computational load, efficiencies must be sought.
I don’t see that we would need to mess with the shaders yet – except for maybe adding north and south poles.
.
Yes, the particles are larger, recycling particles. I'm glad you're seeing some possibilities as well as the difficulties. I'm psyched.
This program contains three strong pluses: a particle engine, a control panel, and an orbital/interactive camera. I’d failed to mention the orbital camera previously. The fact that they all work together after so many of my own previous difficulties makes this program especially noteworthy.
The proto-planet program seems to meet the basic requirements of a mainstream planetary formation model. All particulate matter within a distributed gravitational field of a so-called proto-planet is described by each particle’s: radius, density, gravity, position and velocity.
I don’t know how gravity is handled by the program just yet – it doesn’t look complicated. The controls include a dynamic variable, which you can change as the program is running – gravityConstant. The single value seems to be applied equally to all particles and aggregate particles at the same time. Increased gravity increases particle accelerations, velocities and mergers. Decreased gravity slows things down greatly, too slow and most particles won’t merge. Acceleration is a change in the particle’s velocity in reaction to the field it encounters – such as large nearby particles; all accelerations are currently due to gravity only.
We must add the charge field. This involves two changes to the parameter list.
The Goal. Changing the particle parameter list to include charge repulsion and spin.
First, in accordance with the charge field, as long as we know a particle’s radius, we know its gravity. Gravity increases as the inverse – or inverse squared – distance between particles. If gravity is treated as a field in the program’s calculations then we must compound the acceleration calculation by adding repulsive charge to the same calculation. Note that charge repulsion is not as simple as gravity, since particle emission is a function of a charged particle’s latitude – most repulsion is felt over the equator, and the least repulsion is felt approaching a particle’s pole.
Second. We must include each particle’s spin - the tangential velocity at the particle’s equator. Spin is thus both a position and a velocity. There are alternative possibilities in implementing spin, the best scheme I’ve come up with is monitoring the particles two pole positions – north and south, (with the particle’s position directly in-between). The two poles would then define the particles’ spin-axis. Once again, we need the spin axis of each particle to determine how much charge repulsion each particle feels.
I'll need to study the program first, but that’s my suggested game plan. If we get to the first goal, we’ll discuss further plans then. I think the essentials will be in place. The proto particles will continue to merge, but I believe the observed behavior of the particle field will change greatly. The major drawback is the fact that adding spin adds a great deal more computational load, efficiencies must be sought.
I don’t see that we would need to mess with the shaders yet – except for maybe adding north and south poles.
.
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
Airman. As we know, charge repulsion – bombardment by photons from the earth or from a charged particle - is more than a just a push. The vector you described sounds like the forward push, we also need a spin component. We cannot simulate magnetism without it.Nevyn wrote. The charge field sets the length of the vector and the position of the point determines the direction. The vector is always a repulsion, never an attraction. It can be zero length, but it will always point away from the charged particle. I have an outline for the algorithm, but I haven't coded it and tested it yet
Emission is a function of the particle's latitude, and it will have two components, Vf and Vs. I'm guessing we can determine the magnitudes of the forward and spin components of a particle's emission radiation by directly comparing the two source velocities. Or perhaps some vector addition is in order? We don't need this resolved yet, but we do need to allow for radiative spin.
Anyone?
P.S. Aside from a direct collision, radiative spin is the only mechanism available that can slowly turn the spin axis of the bombarded particle over time. The radiative spin will align all charged particles to the dominant charge source.
.
Last edited by LongtimeAirman on Sun Jun 17, 2018 9:58 pm; edited 1 time in total
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
Most of the work will be in the shaders, as that is where the current gravity math is. But it isn't that bad. Shaders are a pain to debug, but they also represent a smaller world, where math is more significant and easy to use. Once we know what data we need for the calculations, I will find a way to get it into the shader. This will be a little difficult as it needs to be passed as image data (a texture) but don't worry about that for now.
The way I see it, there are 2 parts to an interaction with a charged particle: the effects of the charge field; and the collision with the real particle if the other can get through the charge field. I am working on some math to handle the first and it will not need any spin information. It should be quite quick to calculate. The collision, on the other hand, may need at least some spin calculations, if we want to go to that length. In the first stages, I think we should just model a standard collision. Most of the time will be spent in the charge field calculations (as in the particle needs to overcome that long before it ever reaches a point of collision) and that will be the main driver of the system. That actually may be all we need for collisions. We don't really need to look into spin stacking or any of that.
Having looked over the code for this example, I see that it is based on set time intervals (1/60th of a second) rather than using the actual amount of time that has passed since the last frame. I usually work with the latter, and we may change it at some point, but for now I think it best to just leave it as-is. It does reduce the complexity of the math a bit, which can be beneficial until we get something working.
So what do we need to do to get started? Setup a project in BitBucket so that we can share the code and work on it separately. I'll do that later today, or maybe tomorrow and invite you to the project. While I do that, you can download the source code for the example and get familiar with it (which you probably already have). Once I have the project created, I'll put the original source code in and commit it so that we have the original example as the start of the project. Then you can clone it to your system and make some UI changes such as making the page title reflect this app, remove any unnecessary parts, etc. Just get it ready for the bulk of the work, which will be in the shader math and I still have some things to consider for that.
You might like to get a bit more familiar with shaders and their math. How to use vectors. How to access the position. How attributes and uniforms work and why you would need them. Just keep in mind that in this app, we will be using them for math, not really what they are meant for (which is geometry and color manipulation). We will be using them more like OpenCL, rather than a graphics based thing (which they really are). It's a fudge, but a useful one.
While I could happily take care of the shader parts, that will end up being most of the project and I want it to be your project more than mine. So I might give you the algorithm so that you can implement it in the shader and we can work together to get it running. It will be frustrating and painful and you will tear your hair out, but when it works the way you want, it feels pretty good. I love that feeling.
In response to your recent post, which was added while I was writing this one:
Yes, spin is needed, and I hadn't thought of the magnetic effects. I don't think we need them at first. They can be added in later. I'll see if it can be added in to my math easily. It could just be a boolean value: is it spinning left or right. Maybe a floating point value between -1 and 1 as it will be a sort of spin density, rather than the spin of a single photon. This would mean that at the edge of the charge field the value will be 0 and close to the BPhoton of that particle it will be 1. That should be fairly easy to implement in the math. The result of it will be a quad with the fist 3 items being the emission vector and the 4th item being the spin component.
Off-center hits from the electrical component of the charge field can induce rotation as well. It gets complicated, quickly.
I have always assumed it was the straight bombardment of charge that aligned entities to it rather than the spin. The spin doesn't turn off once something is aligned, but the linear velocities of the charge can become balanced for that entity. That is, if the same amount of charge is hitting it on both sides, then it will not rotate. But if one side is getting more hits, or a more dense field, then it will rotate until they are balanced.
The way I see it, there are 2 parts to an interaction with a charged particle: the effects of the charge field; and the collision with the real particle if the other can get through the charge field. I am working on some math to handle the first and it will not need any spin information. It should be quite quick to calculate. The collision, on the other hand, may need at least some spin calculations, if we want to go to that length. In the first stages, I think we should just model a standard collision. Most of the time will be spent in the charge field calculations (as in the particle needs to overcome that long before it ever reaches a point of collision) and that will be the main driver of the system. That actually may be all we need for collisions. We don't really need to look into spin stacking or any of that.
Having looked over the code for this example, I see that it is based on set time intervals (1/60th of a second) rather than using the actual amount of time that has passed since the last frame. I usually work with the latter, and we may change it at some point, but for now I think it best to just leave it as-is. It does reduce the complexity of the math a bit, which can be beneficial until we get something working.
So what do we need to do to get started? Setup a project in BitBucket so that we can share the code and work on it separately. I'll do that later today, or maybe tomorrow and invite you to the project. While I do that, you can download the source code for the example and get familiar with it (which you probably already have). Once I have the project created, I'll put the original source code in and commit it so that we have the original example as the start of the project. Then you can clone it to your system and make some UI changes such as making the page title reflect this app, remove any unnecessary parts, etc. Just get it ready for the bulk of the work, which will be in the shader math and I still have some things to consider for that.
You might like to get a bit more familiar with shaders and their math. How to use vectors. How to access the position. How attributes and uniforms work and why you would need them. Just keep in mind that in this app, we will be using them for math, not really what they are meant for (which is geometry and color manipulation). We will be using them more like OpenCL, rather than a graphics based thing (which they really are). It's a fudge, but a useful one.
While I could happily take care of the shader parts, that will end up being most of the project and I want it to be your project more than mine. So I might give you the algorithm so that you can implement it in the shader and we can work together to get it running. It will be frustrating and painful and you will tear your hair out, but when it works the way you want, it feels pretty good. I love that feeling.
In response to your recent post, which was added while I was writing this one:
Yes, spin is needed, and I hadn't thought of the magnetic effects. I don't think we need them at first. They can be added in later. I'll see if it can be added in to my math easily. It could just be a boolean value: is it spinning left or right. Maybe a floating point value between -1 and 1 as it will be a sort of spin density, rather than the spin of a single photon. This would mean that at the edge of the charge field the value will be 0 and close to the BPhoton of that particle it will be 1. That should be fairly easy to implement in the math. The result of it will be a quad with the fist 3 items being the emission vector and the 4th item being the spin component.
Airman wrote:Aside from a direct collision, radiative spin is the only mechanism available that can slowly turn the spin axis of the bombarded particle over time. The radiative spin will align all charged particles to the dominant charge source.
Off-center hits from the electrical component of the charge field can induce rotation as well. It gets complicated, quickly.
I have always assumed it was the straight bombardment of charge that aligned entities to it rather than the spin. The spin doesn't turn off once something is aligned, but the linear velocities of the charge can become balanced for that entity. That is, if the same amount of charge is hitting it on both sides, then it will not rotate. But if one side is getting more hits, or a more dense field, then it will rotate until they are balanced.
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
I have created the project and invited you as a developer. Clone the repo and get familiar with it. I copied it from Boids so you should understand the file structure. The readme file explains how to build and deploy, if you want to do it that way but you can just double click the HTML file to run it. I don't see the need for textures (which can create cross site scripting issues) so that shouldn't change.
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
.
Gentle reader, if the above seems a bit overwhelming, join the team. It's almost impossible for me to follow directions until I ask for them. I hit a quick bump to prove it wasn't easy.
I've cloned the repository and made my first change to the html file. Using Sourcetree, I've committed the first change; I see the change was made to the origin/master (not to origin/head). Should I have created a new branch for myself? So I stopped there, I haven't 'Pushed' the 'Commit' yet. I see no change in BitBucket. I expect I should delete and re-clone the repository, then make my own branch?
I've sent a separate message to Nevyn and am awaiting his further instructions.
.
Gentle reader, if the above seems a bit overwhelming, join the team. It's almost impossible for me to follow directions until I ask for them. I hit a quick bump to prove it wasn't easy.
I've cloned the repository and made my first change to the html file. Using Sourcetree, I've committed the first change; I see the change was made to the origin/master (not to origin/head). Should I have created a new branch for myself? So I stopped there, I haven't 'Pushed' the 'Commit' yet. I see no change in BitBucket. I expect I should delete and re-clone the repository, then make my own branch?
I've sent a separate message to Nevyn and am awaiting his further instructions.
.
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
I did not create any branches for this project. You are free to create one if you want to isolate what you are working on, which is a good idea unless doing small edits, but it is not a big deal if you don't. We can work on master and if we need to remove any commits we will just roll it back to where we want it to be.
You didn't do anything wrong. The origin/master tag shows where your local repository is currently at. The origin/head tag shows where the remote repository is at. I can see the remote but I can't see your local repo. If you had pushed that commit then the origin/head tag would move to the same commit as the origin/master tag to show that they are at the same place.
Just remember that you work in your own private repo and that is what you commit to. When you push, then those commits go to the remote repo (BitBucket server) and become public. Commit to save. Push to share.
You didn't do anything wrong. The origin/master tag shows where your local repository is currently at. The origin/head tag shows where the remote repository is at. I can see the remote but I can't see your local repo. If you had pushed that commit then the origin/head tag would move to the same commit as the origin/master tag to show that they are at the same place.
Just remember that you work in your own private repo and that is what you commit to. When you push, then those commits go to the remote repo (BitBucket server) and become public. Commit to save. Push to share.
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
.
The Push worked, good; I'm grateful for the progress.
I finally looked a bit closer at the threejs proto-planet program and I could clearly hear Nevyn say - "you need to learn GLSL".
OK. They start by assuming you know OpenGL. Then, in order to learn OpenGL, you must be familiar with - say, C++.
So, I picked a random Beginner’s OpenGL tutorial.
http://www.opengl-tutorial.org/assets/pdf/opengl_tutorial_2017_06_07.pdf.
It's been a long day, but I'll claim more progress. I’ve updated my drivers, firefox browser, and installed: Visual Studio, CMake and the OpenGLtutorial package. My screen is a bit different, at least the names are the same.

As soon as I find them, I’ll open and play with each of the examples.
.
The Push worked, good; I'm grateful for the progress.
I finally looked a bit closer at the threejs proto-planet program and I could clearly hear Nevyn say - "you need to learn GLSL".
OK. They start by assuming you know OpenGL. Then, in order to learn OpenGL, you must be familiar with - say, C++.
So, I picked a random Beginner’s OpenGL tutorial.
http://www.opengl-tutorial.org/assets/pdf/opengl_tutorial_2017_06_07.pdf.
It's been a long day, but I'll claim more progress. I’ve updated my drivers, firefox browser, and installed: Visual Studio, CMake and the OpenGLtutorial package. My screen is a bit different, at least the names are the same.

As soon as I find them, I’ll open and play with each of the examples.
.
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
It's great to learn OpenGL, but totally not necessary! GLSL is a language within a language. Or it's a language within a framework within a language. Anyway, you won't be seeing any OpenGL stuff in ThreeJS because the point of ThreeJS is to hide all of that from you (which is called WebGL for browsers). Well, you can see it a bit, but not enough to worry about. However, you will, and have, come across GLSL in ThreeJS. You will need to write it directly, but all of the OpenGL stuff is hidden behind the objects that you are using from ThreeJS.
While it is critical to understand the syntax of GLSL, it is also extremely important to understand the execution environment. Where it is executed. How it is executed. What it is executed with respect to. When it will be executed. It will all become apparent by reading a few tutorials on it. Try to find ones that are ThreeJS specific as things can be slightly different in an OpenGL environment. Not enough to stop you from reading them if it is all you can find or just want more info.
Read through a tutorial and then look back at this project. See if you notice any more than you did before. Try another tutorial and see if you understand more. It looks daunting, but once you can answer those questions above it isn't that difficult. And it gives me time to work on the math a bit more.
While it is critical to understand the syntax of GLSL, it is also extremely important to understand the execution environment. Where it is executed. How it is executed. What it is executed with respect to. When it will be executed. It will all become apparent by reading a few tutorials on it. Try to find ones that are ThreeJS specific as things can be slightly different in an OpenGL environment. Not enough to stop you from reading them if it is all you can find or just want more info.
Read through a tutorial and then look back at this project. See if you notice any more than you did before. Try another tutorial and see if you understand more. It looks daunting, but once you can answer those questions above it isn't that difficult. And it gives me time to work on the math a bit more.
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
.
Thanks for the timely directions Nevyn. I’ve tried concentrating more on GLSL and three.js, and am currently in part two of A Beginner's Guide to Coding Graphics Shaders by Omar Shehata. https://gamedevelopment.tutsplus.com/series/a-beginners-guide-to-coding-graphics-shaders--cms-834.
As proof of progress, I finally wrote/modified/created my own blank app - threejs ready html file – I didn’t need their’s! For example, in following part two I’m making changes to my file with notepad++ while viewing the browser output and developer console, very satisfying.
The lessons and videos I've looked at favor fragment (or pixel) shaders. I remember having seen and mentioning Shadertoy https://www.shadertoy.com to you guys before; but in following part one I spent my first time playing with the https://www.shadertoy.com/new editor. I can't believe all the fun we're having lately.
Here are a few new references that I found in a new reference. If you know any good sources - where vertex shaders are used for particle computations - please share.
1. The Book of Shaders, by Patricio Gonzalez Vivo and Jen Lowe.
https://thebookofshaders.com/. “This is a gentle step-by-step guide through the abstract and complex universe of Fragment Shaders”.
2. IQ’s articles (rendering techniques, useful maths, coding hacks…)
http://www.iquilezles.org/index.html
3. OpenGL and OpenGL
and OpenGL ES Reference Pages
ES Reference Pages
https://www.khronos.org/registry/OpenGL-Refpages/
Complete descriptions of API commands and shading language functions are provided for the current versions these APIs.
.
Nevyn wrote. Read through a tutorial and then look back at this project. See if you notice any more than you did before. Try another tutorial and see if you understand more. It looks daunting, but once you can answer those questions above it isn't that difficult. And it gives me time to work on the math a bit more.
Thanks for the timely directions Nevyn. I’ve tried concentrating more on GLSL and three.js, and am currently in part two of A Beginner's Guide to Coding Graphics Shaders by Omar Shehata. https://gamedevelopment.tutsplus.com/series/a-beginners-guide-to-coding-graphics-shaders--cms-834.
As proof of progress, I finally wrote/modified/created my own blank app - threejs ready html file – I didn’t need their’s! For example, in following part two I’m making changes to my file with notepad++ while viewing the browser output and developer console, very satisfying.
The lessons and videos I've looked at favor fragment (or pixel) shaders. I remember having seen and mentioning Shadertoy https://www.shadertoy.com to you guys before; but in following part one I spent my first time playing with the https://www.shadertoy.com/new editor. I can't believe all the fun we're having lately.
Here are a few new references that I found in a new reference. If you know any good sources - where vertex shaders are used for particle computations - please share.
1. The Book of Shaders, by Patricio Gonzalez Vivo and Jen Lowe.
https://thebookofshaders.com/. “This is a gentle step-by-step guide through the abstract and complex universe of Fragment Shaders”.
2. IQ’s articles (rendering techniques, useful maths, coding hacks…)
http://www.iquilezles.org/index.html
3. OpenGL
 and OpenGL
and OpenGL ES Reference Pages
ES Reference Pageshttps://www.khronos.org/registry/OpenGL-Refpages/
Complete descriptions of API commands and shading language functions are provided for the current versions these APIs.
.
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
Just a quick update to let you know that I have been working on the math for this, but haven't had a lot of time for it lately. You threw me a curve ball when you mentioned magnetism and I am trying to fit it in somehow, but not seeing a nice and clear path yet.
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
.
Thanks Nevyn, no rush. I haven’t gotten much further yet either. I’ve made some pretty, time varying shaders but I haven’t imported any textures yet – that’s next, and uniforms. I’ve also found a couple more shader particle engines I’ll be able to study – including the “other” threejs Bird Flocking example.
I’m still considering the problem of a charged particle parameter list.
Proto-planet’s observed mass presumably add up to a planet - we are just adding charge. If so, the unseen photons out mass the observed mass twenty to one. Even though Proto-planet’s initial charged particles shown have mass radii much larger than the proton scale, we can assume that they follow charged particle, charge recycling rules; such as, charge mainly enters the particle’s poles and is emitted mainly from the particle’s equator.
Proto-planet begins with a random distribution of observed mass within a cylindrical volume of space. Is that how the charge field would organize things, or does it make charge field sense? What are the ambient conditions?
I believe we (Jared, you, (maybe even Licht and Ciaolo too) and I had a good discussion on this subject way back in March https://milesmathis.forumotion.com/t444-the-sun-s-galactic-orbit-and-charge-field-implications. Planetary charge recycling in our solar system includes direct - say Sol to Earth insolation - and indirect, charge not direct from Sol, such as charge recycling/intake - matter will spin upward and antimatter will spin downward – into the planetary poles. I don’t see how to model unseen charge entering poles just yet.
Appropriate ambient conditions may require a large charged particle – such as Sol, or the “Center of the Galaxy” - with both a large angular aspect and a strong gravitational/charge presence. I suppose it may be distant or central to Proto-planet’s initial mass distribution. This is just discussion at present.
We may naturally try to consider the particles shown as large radii, A-spin, b-photons. Our large particles might also be non-spherical X spins. I don’t know whether a quantization of all spin radius values makes sense yet or not. If we do include such info we may be able to transition to smaller scales more easily.
Distances separating particles may be comparable to the scale of the Earth/moon system or larger. I suspect that means relativity must come into effect. Luckily, the joys of modeling include simplifications - we can ignore time delay, or include it - someday. I agree with you, wherever possible, we should strive to include real time.
I think we should “know” the approximate received photon density between particles. I spoke of radiation spin knowing we are sampling large numbers of photons over some time differential. Most – though not all - emissions exchanged between equal and average particles will tend to spin cancel over time, magnetic emissions do not cancel in the same way. Magnetism may need to be included as a new parameter related to density. I suppose as a particle becomes more magnetic, more coherent emissions would be received from that source, with more efficient transfer of each photon’s tangential spin energy. Note that the emission field - or magnetic field - of large particles are actually dual toroidal fields.
.
Thanks Nevyn, no rush. I haven’t gotten much further yet either. I’ve made some pretty, time varying shaders but I haven’t imported any textures yet – that’s next, and uniforms. I’ve also found a couple more shader particle engines I’ll be able to study – including the “other” threejs Bird Flocking example.
I’m still considering the problem of a charged particle parameter list.
Proto-planet’s observed mass presumably add up to a planet - we are just adding charge. If so, the unseen photons out mass the observed mass twenty to one. Even though Proto-planet’s initial charged particles shown have mass radii much larger than the proton scale, we can assume that they follow charged particle, charge recycling rules; such as, charge mainly enters the particle’s poles and is emitted mainly from the particle’s equator.
Proto-planet begins with a random distribution of observed mass within a cylindrical volume of space. Is that how the charge field would organize things, or does it make charge field sense? What are the ambient conditions?
I believe we (Jared, you, (maybe even Licht and Ciaolo too) and I had a good discussion on this subject way back in March https://milesmathis.forumotion.com/t444-the-sun-s-galactic-orbit-and-charge-field-implications. Planetary charge recycling in our solar system includes direct - say Sol to Earth insolation - and indirect, charge not direct from Sol, such as charge recycling/intake - matter will spin upward and antimatter will spin downward – into the planetary poles. I don’t see how to model unseen charge entering poles just yet.
Appropriate ambient conditions may require a large charged particle – such as Sol, or the “Center of the Galaxy” - with both a large angular aspect and a strong gravitational/charge presence. I suppose it may be distant or central to Proto-planet’s initial mass distribution. This is just discussion at present.
We may naturally try to consider the particles shown as large radii, A-spin, b-photons. Our large particles might also be non-spherical X spins. I don’t know whether a quantization of all spin radius values makes sense yet or not. If we do include such info we may be able to transition to smaller scales more easily.
Distances separating particles may be comparable to the scale of the Earth/moon system or larger. I suspect that means relativity must come into effect. Luckily, the joys of modeling include simplifications - we can ignore time delay, or include it - someday. I agree with you, wherever possible, we should strive to include real time.
I think we should “know” the approximate received photon density between particles. I spoke of radiation spin knowing we are sampling large numbers of photons over some time differential. Most – though not all - emissions exchanged between equal and average particles will tend to spin cancel over time, magnetic emissions do not cancel in the same way. Magnetism may need to be included as a new parameter related to density. I suppose as a particle becomes more magnetic, more coherent emissions would be received from that source, with more efficient transfer of each photon’s tangential spin energy. Note that the emission field - or magnetic field - of large particles are actually dual toroidal fields.
.
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
I'm a little confused on where you want this app to go. I was thinking that we are trying to model charged particles such as electrons and protons. Not planets. So the bright spheres in this app would become the protons and we would introduce code to represent the charge field interactions of the particles. This means that the charge field does not exist in the model, it is abstracted by the code. That is, you don't see the charge photons and we don't have them in memory either. They are just part of the calculation between interacting particles. Just in the math. In essence, the math would boil down to charge densities and a given particle would move based on the densities around it.
I am trying to create an algorithm that calculates the charge density at some point from the particle emitting that charge. This takes the equator to pole differences into account. Once that is done, the main algorithm will look like this:
That is a very basic overview of it. I also want to bring in the ambient field which will be a set density from all directions except where there is another particle in the way. Still not sure how to do that specifically. Maybe I will just model it as an attraction to where other particles are, rather than a repulsion from everywhere except where they are not. That seems like it will be easier to work with and amounts to the same thing.
I'm just not sure how to add spin to that. I'm not sure of what the spin is going to do. I'm not even convinced that magnetism exists at this level. Yes, it exists on the charge photons, but what we call magnetism in something that atoms do, not particles. Even when particles react to magnetism, they are doing so by magnetism created by atoms and molecules. I am tempted to just ignore it for now and see how things look with just the charge interactions.
To be a bit clearer, I think it takes a high charge density for the spin to become magnetism. The charge channels of atoms and molecules can create this coherence and density but I am not convinced that a lone proton can do it. However, each individual charge photon does have that spin component, so there are going to be some effects from it in reality, but is it enough to worry about modeling or are they small enough to ingore?
Happy to hear anyone's thoughts on that, though. I could just be trying to convince myself that I don't have to deal with it.
I am trying to create an algorithm that calculates the charge density at some point from the particle emitting that charge. This takes the equator to pole differences into account. Once that is done, the main algorithm will look like this:
- Code:
for each particle // this loop is actually handled by the shader framework
{
vector v = this particles velocity
for each other particle
{
calculate charge density of 'other particle' at position of 'this particle'
add to v, possibly scaling
}
this particles velocity = v
}
That is a very basic overview of it. I also want to bring in the ambient field which will be a set density from all directions except where there is another particle in the way. Still not sure how to do that specifically. Maybe I will just model it as an attraction to where other particles are, rather than a repulsion from everywhere except where they are not. That seems like it will be easier to work with and amounts to the same thing.
I'm just not sure how to add spin to that. I'm not sure of what the spin is going to do. I'm not even convinced that magnetism exists at this level. Yes, it exists on the charge photons, but what we call magnetism in something that atoms do, not particles. Even when particles react to magnetism, they are doing so by magnetism created by atoms and molecules. I am tempted to just ignore it for now and see how things look with just the charge interactions.
To be a bit clearer, I think it takes a high charge density for the spin to become magnetism. The charge channels of atoms and molecules can create this coherence and density but I am not convinced that a lone proton can do it. However, each individual charge photon does have that spin component, so there are going to be some effects from it in reality, but is it enough to worry about modeling or are they small enough to ingore?
Happy to hear anyone's thoughts on that, though. I could just be trying to convince myself that I don't have to deal with it.
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
.
I mainly want to see charged particle interactions, regardless of the scale, proton or planet.
Yes, I see that this program abstracts photons as charge density emitted and received by the observed particles shown on the screen. We don’t need to worry about “indirect” charge entering the particle poles. It’s the “direct” photon collisions that result in accelerations – changes in direction and velocity - to both the forward velocity as well as the tangential spins of the particles present.
Please consider, the simplest demonstration of the order resulting from the charged field vice the gravitational field alone is shown with just two equal sized charged particles. Depending on their initial positions and velocities, they will begin to orbit or wildly swing past each other. Their close passes will cause each of their spin axii to shift. We must include a mechanism – i.e. magnetism – that allows particles to shift their spin axii without direct collisions.
It seems likely to me that over time all particle spins present will tend to a single spin axis. Magnetism is important in determining how long it takes for the interacting charged particles to reach their long term equilibrium.
Suggest changing your code’s “calculate” line from:
There’s no good reason to leave magnetism out of the calculation.
I'd also welcome additional opinions.
.
I mainly want to see charged particle interactions, regardless of the scale, proton or planet.
Yes, I see that this program abstracts photons as charge density emitted and received by the observed particles shown on the screen. We don’t need to worry about “indirect” charge entering the particle poles. It’s the “direct” photon collisions that result in accelerations – changes in direction and velocity - to both the forward velocity as well as the tangential spins of the particles present.
Please consider, the simplest demonstration of the order resulting from the charged field vice the gravitational field alone is shown with just two equal sized charged particles. Depending on their initial positions and velocities, they will begin to orbit or wildly swing past each other. Their close passes will cause each of their spin axii to shift. We must include a mechanism – i.e. magnetism – that allows particles to shift their spin axii without direct collisions.
It seems likely to me that over time all particle spins present will tend to a single spin axis. Magnetism is important in determining how long it takes for the interacting charged particles to reach their long term equilibrium.
Suggest changing your code’s “calculate” line from:
- Code:
calculate charge density of 'other particle' at position of 'this particle'
- Code:
calculate the 3 accelerations due to charge density and gravity of 'other particle' at position of 'this particle'
There’s no good reason to leave magnetism out of the calculation.
I'd also welcome additional opinions.
.
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
LongtimeAirman wrote:
Please consider, the simplest demonstration of the order resulting from the charged field vice the gravitational field alone is shown with just two equal sized charged particles. Depending on their initial positions and velocities, they will begin to orbit or wildly swing past each other. Their close passes will cause each of their spin axii to shift. We must include a mechanism – i.e. magnetism – that allows particles to shift their spin axii without direct collisions.
It seems likely to me that over time all particle spins present will tend to a single spin axis. Magnetism is important in determining how long it takes for the interacting charged particles to reach their long term equilibrium.
Why would all particles tend to a single spin axis? What stops them from spinning? What are they aligning to? The spin doesn't stop just because the other particle is in some alignment. In your scenario above, the 2 particles would impart spin to each other and it will never stop. In fact, it would keep getting faster and faster until both particles are spinning at c.
LongtimeAirman wrote:
Suggest changing your code’s “calculate” line from:
to:
- Code:
calculate charge density of 'other particle' at position of 'this particle'
- Code:
calculate the 3 accelerations due to charge density and gravity of 'other particle' at position of 'this particle'
I was only outlining the charge interaction code. The gravity code is already present and doesn't need discussion (yet).
LongtimeAirman wrote:
There’s no good reason to leave magnetism out of the calculation.
Being inconsequential is a good enough reason. Making progress without unnecessary complications is a good enough reason. We can always add it in later, once we have a more solid understanding of how it effects the entities in the field.
We also don't actually need spin in order to create spin. We can use imbalanced charge fields to accomplish the same thing and it comes with a way to actually align things. In the above pseudo-code, I said that each particle will measure the other particle from its own position. I have been thinking about calculating the charge densities from a number of positions around the particle, rather than just from its center. If we measure the charge field from the N,S,E,W,F,B of the particle, we can see how they balance with respect to the orientation of the particle. So if the east and west sides have charge vectors in opposite directions, then the particle will spin. If they were in the same direction, then the particle would move.
I understand the desire to include everything at once, but it leads to stagnation when things get too complex to handle. An iterative approach often leads to a better system as you build on top of what you have. It is easier to fiddle with something that is operational than it is to create it all at once. It allows you to focus on one thing at a time as you add it into the system.
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
.
Thanks for explaining things so clearly.
“I believe that all particles will tend to a common spin” is just a reasonable expectation – our own solar system appears to be an example - of the ability of particles to alter the spin direction and velocities of other particles. If radiative spin, or magnetism, is the only means available to change spins, why give it up? But I’m wrong. Your observation that spin can be changed by a differential mechanism far more effectively than the magnetism idea I’ve been defending is great news. Why didn’t you say so sooner?
I like your idea of monitoring the particle’s N,S,E,W,F,B a lot. I'll admit I need to give it more thought.
Your patience is appreciated.
.
Thanks for explaining things so clearly.
“I believe that all particles will tend to a common spin” is just a reasonable expectation – our own solar system appears to be an example - of the ability of particles to alter the spin direction and velocities of other particles. If radiative spin, or magnetism, is the only means available to change spins, why give it up? But I’m wrong. Your observation that spin can be changed by a differential mechanism far more effectively than the magnetism idea I’ve been defending is great news. Why didn’t you say so sooner?
I like your idea of monitoring the particle’s N,S,E,W,F,B a lot. I'll admit I need to give it more thought.
Your patience is appreciated.
.
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
.
Status update. Still poking away at GLSL with a Three.js platform, I enjoy it well enough. I see how every mistake results in the same failure to compile error – no clues as to why. Glad I’ve got a wide autistic streak.
I’ve mainly spent several hours with The Book of Shaders, by Patricio Gonzalez Vivo & Jen Lowe, page 05. https://thebookofshaders.com/05/ The Algorithmic drawing page, which includes: Shaping functions, Step and Smoothstep, Sine and Cosine, Some extra useful functions, and Advance shaping functions; and links.
The reader is introduced to built-in math functions. Dividing the screen by the resolution gives one the normalized st.xy. y can be a function of st.x. I wasn’t aware of how one might plot functions in Three.js. Learning how to do so in shader language is a surprise. I have a few small problems, such as #define PI 3.14159265359; // Error, I must use 3.1415926535 instead of PI. The author insists we develop good GLSL karate skills by painting Mr. Miyagi’s fence, by recreating 35 power plots. I complied. Doubling the normalized st.x values then offsetting them by 0.5 to get the desired -1.0 <=x<=1.0 range was the main trick. The deeper lesson is the fact that single 'dimensional' functions are valuable graphics tools that may be implemented in various ways, beyond my current awareness. I'm sure Maya does these sorts of thing much easier GLSL.
I gave 06 Colors page a brief once over. The author makes many challenges without answers. I’ll go to 07 https://thebookofshaders.com/07/, Shapes, next.
.
Status update. Still poking away at GLSL with a Three.js platform, I enjoy it well enough. I see how every mistake results in the same failure to compile error – no clues as to why. Glad I’ve got a wide autistic streak.
I’ve mainly spent several hours with The Book of Shaders, by Patricio Gonzalez Vivo & Jen Lowe, page 05. https://thebookofshaders.com/05/ The Algorithmic drawing page, which includes: Shaping functions, Step and Smoothstep, Sine and Cosine, Some extra useful functions, and Advance shaping functions; and links.
The reader is introduced to built-in math functions. Dividing the screen by the resolution gives one the normalized st.xy. y can be a function of st.x. I wasn’t aware of how one might plot functions in Three.js. Learning how to do so in shader language is a surprise. I have a few small problems, such as #define PI 3.14159265359; // Error, I must use 3.1415926535 instead of PI. The author insists we develop good GLSL karate skills by painting Mr. Miyagi’s fence, by recreating 35 power plots. I complied. Doubling the normalized st.x values then offsetting them by 0.5 to get the desired -1.0 <=x<=1.0 range was the main trick. The deeper lesson is the fact that single 'dimensional' functions are valuable graphics tools that may be implemented in various ways, beyond my current awareness. I'm sure Maya does these sorts of thing much easier GLSL.
I gave 06 Colors page a brief once over. The author makes many challenges without answers. I’ll go to 07 https://thebookofshaders.com/07/, Shapes, next.
.
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
While that is all great to learn, you really just need to be able to specify the math in the GLSL language and to know what data you are given, what data you pass in yourself and what you can pass back out. Most things you come across will NOT output anything because that is not the normal usage of a shader. They are meant to alter the positions of a vertex in a geometry, so you just normally set the position (which is given to you by the framework and you just set its values).
Be careful of slight changes to the language over different versions. The tutorials you find may be a bit old and the language has moved on. Also be careful of what the code is doing as the way it operates is quite different to what most modern language do. Mostly this is because you have direct access to pointers, which are awesome and horrible all at the same time. Most languages hide them from you these days, but in C (which GLSL is a variant of) you have to deal with them.
Maybe an example will help. Suppose we created a vector and called it v1. Then we decalre another vector, called v2, and make it equal to v1. Then we change the x value of v2.
What do you think v1.x will be at this point?
In most modern languages, it would be 5, because each vector is a reference to an object and when we assigned v1 to v2, we just copied the reference (or pointer) so both v1 and v2 actually refer to the same object. However, in C, this is not the case. When v2 was made equal to v1, it actually created a new vector and copied the values from v1 into it. So v1 and v2 are totally different objects and v1.x will still equal 1.
We can accomplish what modern language do in C though. We have to use pointers for this.
After that code has executed, both v1.x and v2.x will be 5 because both v1 and v2 refer to the same object. Let me explain the changes.
Firstly, v2 is not a vector anymore, it is a pointer to a vector. We declare this with the * after the data type. It says that this variable is a pointer and can only point to other variables that are of type vec3.
Secondly the assigning of v1 to v2 now has an & in front of the v1 variable. That is the Address operator. It is used to return the address of a variable rather than the variable itself. So in essence, that line says 'get the address of v1 and copy it into v2'. Only the address, not the data.
Thirdly, the line that changes the x variable uses an arrow rather than a dot. That is the De-referencing operator. It is used to say that we want to access a field within an object, x in this case, but we have a pointer so first use the pointer to find the object and then return the x value of that object. If we used the dot operator, it would have put the value 5 into a memory location that does not represent the x value of v1 (except by accident). This is how hackers create a Buffer Overflow and access memory that they are not supposed to (only they use an array, hence buffer, and look beyond it, hence overflow).
As you can probably tell, C does not restrict you from doing what you told it you wanted to do. It does not make sure that you are referencing a valid object, it just assumes that you are and performs its job. This is why C/C++ applications are fast. It is also why they are error prone.
Why is all of this pointer stuff relevant? Because you might be thinking that you are changing something that you are not. This is especially important when passing data from one function to another. Let's assume that you wanted to pass a vector to another function that changes it for you. A pretty common thing to do. You might do something like this:
In your main function, you call that function like this:
After that has executed, you think that v1 should equal (2, 4, 6), but it still equals (1, 2, 3). That is because C always uses 'pass by value', as opposed to 'pass by reference', unless told to. So when you called doubleIt( v ), it actually created a new vec3 object, copied the content of v into it, and passed that to the function. The function then altered that temporary copy and so you don't see any change to your vector.
There are 2 ways to solve this: return the result from the doubleIt function; or pass in a pointer.
Returning the result:
OR
Pass a pointer:
Using a pointer is the fastest method, as it only needs to copy the pointer, not the whole vector. It also doesn't have to return anything, which involves more copying.
As an FYI, the size of a pointer is dependent on the OS being used. This is what it means to be 32bit or 64bit. That refers to the size of an address of a single memory location (and hence how much memory you can access) and a pointer is a memory location so it will be 32 bits on a 32 bit system.
There is more funky stuff you can do with pointers, such as pointer arithmetic, but I don't want to confuse you even more. Suffice to say that most modern languages hide a lot of this from you because you can stuff things up pretty quick. Modern languages call them References, rather than pointers, and you can't do any arithmetic on them. They just reference an object. For example, in Java, every object is actually a reference. Primitives like int, long, float, double, boolean, etc, are not references, but everything else is. When you pass a reference to a function in Java, it gets the reference and not the object (but can access it through the reference). So the first code block above would work in Java, but not in C, because the vector would be an object and the variable would be a pointer, even though you can't tell that it is from the syntax. I often stuff up my C code because I am so used to Java.
I don't know if that is at all related to your problems, but it might help.
Be careful of slight changes to the language over different versions. The tutorials you find may be a bit old and the language has moved on. Also be careful of what the code is doing as the way it operates is quite different to what most modern language do. Mostly this is because you have direct access to pointers, which are awesome and horrible all at the same time. Most languages hide them from you these days, but in C (which GLSL is a variant of) you have to deal with them.
Maybe an example will help. Suppose we created a vector and called it v1. Then we decalre another vector, called v2, and make it equal to v1. Then we change the x value of v2.
- Code:
vec3 v1 = vec3(1, 2, 3);
vec3 v2 = v1;
v2.x = 5;
What do you think v1.x will be at this point?
In most modern languages, it would be 5, because each vector is a reference to an object and when we assigned v1 to v2, we just copied the reference (or pointer) so both v1 and v2 actually refer to the same object. However, in C, this is not the case. When v2 was made equal to v1, it actually created a new vector and copied the values from v1 into it. So v1 and v2 are totally different objects and v1.x will still equal 1.
We can accomplish what modern language do in C though. We have to use pointers for this.
- Code:
vec3 v1 = vec4(1, 2, 3);
vec3* v2 = &v1;
v2->x = 5;
After that code has executed, both v1.x and v2.x will be 5 because both v1 and v2 refer to the same object. Let me explain the changes.
Firstly, v2 is not a vector anymore, it is a pointer to a vector. We declare this with the * after the data type. It says that this variable is a pointer and can only point to other variables that are of type vec3.
Secondly the assigning of v1 to v2 now has an & in front of the v1 variable. That is the Address operator. It is used to return the address of a variable rather than the variable itself. So in essence, that line says 'get the address of v1 and copy it into v2'. Only the address, not the data.
Thirdly, the line that changes the x variable uses an arrow rather than a dot. That is the De-referencing operator. It is used to say that we want to access a field within an object, x in this case, but we have a pointer so first use the pointer to find the object and then return the x value of that object. If we used the dot operator, it would have put the value 5 into a memory location that does not represent the x value of v1 (except by accident). This is how hackers create a Buffer Overflow and access memory that they are not supposed to (only they use an array, hence buffer, and look beyond it, hence overflow).
As you can probably tell, C does not restrict you from doing what you told it you wanted to do. It does not make sure that you are referencing a valid object, it just assumes that you are and performs its job. This is why C/C++ applications are fast. It is also why they are error prone.
Why is all of this pointer stuff relevant? Because you might be thinking that you are changing something that you are not. This is especially important when passing data from one function to another. Let's assume that you wanted to pass a vector to another function that changes it for you. A pretty common thing to do. You might do something like this:
- Code:
void doubleIt(vec3 v)
{
v.x *= 2;
v.y *= 2;
v.z *= 2;
}
In your main function, you call that function like this:
- Code:
vec3 v = vec3(1, 2, 3);
doubleIt( v );
After that has executed, you think that v1 should equal (2, 4, 6), but it still equals (1, 2, 3). That is because C always uses 'pass by value', as opposed to 'pass by reference', unless told to. So when you called doubleIt( v ), it actually created a new vec3 object, copied the content of v into it, and passed that to the function. The function then altered that temporary copy and so you don't see any change to your vector.
There are 2 ways to solve this: return the result from the doubleIt function; or pass in a pointer.
Returning the result:
- Code:
vec3 doubleIt(vec3 v)
{
v.x *= 2;
v.y *= 2;
v.z *= 2;
return v;
}
void main()
{
vec3 v = vec3(1, 2, 3);
v = doubleIt( v );
}
OR
Pass a pointer:
- Code:
void doubleIt(vec3* v)
{
v->x *= 2;
v->y *= 2;
v->z *= 2;
}
void main()
{
vec3 v = vec3(1, 2, 3);
doubleIt( &v );
}
Using a pointer is the fastest method, as it only needs to copy the pointer, not the whole vector. It also doesn't have to return anything, which involves more copying.
As an FYI, the size of a pointer is dependent on the OS being used. This is what it means to be 32bit or 64bit. That refers to the size of an address of a single memory location (and hence how much memory you can access) and a pointer is a memory location so it will be 32 bits on a 32 bit system.
There is more funky stuff you can do with pointers, such as pointer arithmetic, but I don't want to confuse you even more. Suffice to say that most modern languages hide a lot of this from you because you can stuff things up pretty quick. Modern languages call them References, rather than pointers, and you can't do any arithmetic on them. They just reference an object. For example, in Java, every object is actually a reference. Primitives like int, long, float, double, boolean, etc, are not references, but everything else is. When you pass a reference to a function in Java, it gets the reference and not the object (but can access it through the reference). So the first code block above would work in Java, but not in C, because the vector would be an object and the variable would be a pointer, even though you can't tell that it is from the syntax. I often stuff up my C code because I am so used to Java.
I don't know if that is at all related to your problems, but it might help.
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
I believe that I have made an important break-through in developing the charge field algorithm for this project. The funny thing is that I had to make the exact same break-through that I made for the algorithm that calculates the charge field densities at some position from a particle.
Essentially, there are 2 algorithms in use here. The first one is used to calculate the charge density of a particle at some point. The second one makes use of that to calculate the charge density from 6 positions on the edge of the particle (N, S, E, W, F, B) and then uses that to determine the changes required to the linear velocity and spin components of the particle.
When I was thinking about the charge density algorithm, I realised that I could break the vector up into 2 parts: the Y component; and the XZ components (assuming the particle is oriented with its North pole in the +Y dimension). The ratio of these components is used to determine whether we are looking at an equator or pole position or some variation in between. This then effects the charge density value to be returned.
I finally realised that I can do the same thing for the 6 positioned vectors calculated in the second algorithm. I split them up into Velocity and Spin components. I'll try to write it up for you guys to peruse.
Essentially, there are 2 algorithms in use here. The first one is used to calculate the charge density of a particle at some point. The second one makes use of that to calculate the charge density from 6 positions on the edge of the particle (N, S, E, W, F, B) and then uses that to determine the changes required to the linear velocity and spin components of the particle.
When I was thinking about the charge density algorithm, I realised that I could break the vector up into 2 parts: the Y component; and the XZ components (assuming the particle is oriented with its North pole in the +Y dimension). The ratio of these components is used to determine whether we are looking at an equator or pole position or some variation in between. This then effects the charge density value to be returned.
I finally realised that I can do the same thing for the 6 positioned vectors calculated in the second algorithm. I split them up into Velocity and Spin components. I'll try to write it up for you guys to peruse.
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
Nevyn wrote. While that is all great to learn, you really just need to be able to specify the math in the GLSL language and to know what data you are given, what data you pass in yourself and what you can pass back out.
...
I don't know if that is at all related to your problems, but it might help.
Thanks Nevyn. I’m familiar enough with the pain and joys of programming to know that your detailed replies to my “few small problems” will help mightily. My current problems include no experience with C, and not having given more than half a thought to programming pointers, buffers, or passing data. While I’m on a tangent, enjoying this learning opportunity, I’ve also learned it’s more important to keep your directions in mind - I added the appropriate bold to your quote above.
Nevyn wrote. I believe that I have made an important break-through in developing the charge field algorithm for this project.
…
I'll try to write it up for you guys to peruse.
Great, let's see what you’ve got in mind. I'll draw the vector diagrams if you like. It should be easy to show how, given an emitting charged particle, a nearby particle will receive slightly varying direct charge densities at each of its N,S,E,W,F,B set of ortho-compass points. That variance - or differential – gets stronger the smaller the distance (d) between the two particles, at 1/d^3 or 1/d^4. Can't help but notice you mentioned the spin component in the received charge density.
.
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
I did mention the spin component, but not the one you are thinking of. That was not meant to be the spin of the charge photons, but the spin of the central particle, such as a proton. It is just trying to induce spin based on the surrounding charge densities. Basically I am letting each cardinal point act like it is a separate entity, but it will effect, and be effected by, the other points. I'm still figuring out how that math looks but I think the rest of the algorithm is getting close to operational. I haven't actually coded any of this. I'm just playing with ideas at this stage.
With respect to coding the math, we are going to be working with vectors and matrices. I don't believe GLSL has a matrix object yet. I know they were looking into it for OpenCL (which is very close to GLSL but it is for computing, not shaders). Therefore we will need to handle the matrix math ourselves. I already have some routines for that, but you might want to look into it yourself to get familiar with them. The main problem is whether the matrices are row-major or column-major. Most things are row-major but you will come across some column-major matrices if you play with 3D systems long enough. Even within the same framework (such as ThreeJS), you can get a mix of them as the camera systems usually use column-major because it is easier to work with in that instance.
We are also going to be working with images. Not really as image data, but as a transport mechanism. This is how we will pass some of the data in and out. It is the only way to get data out but there are other options to get it in. We wouldn't need images in OpenCL, but we are working in a shader framework, not computing, so we have to make do with what we have. I will take care of that part, but it doesn't hurt to be familiar with how image data works in these systems. You can find many image manipulation routines for OpenCL. The code should be virtually identical, close enough to get the idea.
While I still don't know the specifics, I have a general idea that we are going to have to pass in a lot of data through images. I am thinking that I will create the functions that we will need and the code to retrieve the data from the images and put it back in, but let you implement the actual algorithm from my specification. That will be tricky enough without having to understand the transport mechanism as well. Of course, I will also implement it on my own, for testing if nothing else, but I want you to get a feel for converting the math into code.
With respect to coding the math, we are going to be working with vectors and matrices. I don't believe GLSL has a matrix object yet. I know they were looking into it for OpenCL (which is very close to GLSL but it is for computing, not shaders). Therefore we will need to handle the matrix math ourselves. I already have some routines for that, but you might want to look into it yourself to get familiar with them. The main problem is whether the matrices are row-major or column-major. Most things are row-major but you will come across some column-major matrices if you play with 3D systems long enough. Even within the same framework (such as ThreeJS), you can get a mix of them as the camera systems usually use column-major because it is easier to work with in that instance.
We are also going to be working with images. Not really as image data, but as a transport mechanism. This is how we will pass some of the data in and out. It is the only way to get data out but there are other options to get it in. We wouldn't need images in OpenCL, but we are working in a shader framework, not computing, so we have to make do with what we have. I will take care of that part, but it doesn't hurt to be familiar with how image data works in these systems. You can find many image manipulation routines for OpenCL. The code should be virtually identical, close enough to get the idea.
While I still don't know the specifics, I have a general idea that we are going to have to pass in a lot of data through images. I am thinking that I will create the functions that we will need and the code to retrieve the data from the images and put it back in, but let you implement the actual algorithm from my specification. That will be tricky enough without having to understand the transport mechanism as well. Of course, I will also implement it on my own, for testing if nothing else, but I want you to get a feel for converting the math into code.
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
Here are my very rough notes for the second algorithm. The first algorithm is used to calculate the charge density at some point from the source particle. In this algorithm, we are using that to find the charge density of all other particles from the perspective of this particle.
Conditions and setup:
Each particle is treated as if it was in a set orientation such that its North pole is +Y, East is +X and Front is +Z.
We want all calculations to be performed in this orientation so that we can split some vectors easily.
We will need to transform all other particles into this virtual coordinate system.
We do that by taking the orientation transform of this particle, inverting it, and applying to each other particle.
This will not actually change those particles, but will change the values in the temporary data we have for them.
Algorithm:
For linear velocity:
For spin velocity:
The linear velocity will need to be converted back into the working coordinate system. This should just involve applying the original orientation transform to the results. The spin component should not matter.
Charge Density Model
Given a particle, determine the charge field effects of other particles on it.
Conditions and setup:
Each particle is treated as if it was in a set orientation such that its North pole is +Y, East is +X and Front is +Z.
We want all calculations to be performed in this orientation so that we can split some vectors easily.
We will need to transform all other particles into this virtual coordinate system.
We do that by taking the orientation transform of this particle, inverting it, and applying to each other particle.
This will not actually change those particles, but will change the values in the temporary data we have for them.
Algorithm:
- Code:
Calculate sum of charge densities from other particles at the cardinal positions on this particle (N,S,E,W,F,B).
For each position:
Split charge vector into 3 components: 1 linear velocity component that points to the center of the particle; 2 spin components that point in the other 2 dimensions.
The actual dimensions used are different for each position:
North: V=-Y, S=X,Z
South: V=+Y, S=X,Z
East: V=-X, S=Y,Z
West: V=+X, S=Y,Z
Front: V=+Z, S=X,Y
Back: V=-Z, S=X,Y
Where a vector with the same sign as the linear velocity dimension means a repulsion and the opposite means attraction (or do we ignore attraction and just let the other side apply repulsion?).
The spin components work in both directions and just changes the angle from positive to negative.
For linear velocity:
- Code:
We now have 6 vectors positioned at 6 positions.
We reduce that to 1 vector by summing them all to find the resultant velocity.
May need to ignore vectors that point away from the center of the particle (attraction).
Add to the particles current velocity.
For spin velocity:
- Code:
We now have 12 vectors at 6 positions.
We need to reduce that to 3 angles about 3 axes.
First we reduce each opposite pair to 2 vectors for each pair.
Note that each opposite pair uses the same spin dimensions, but in opposite ways. So a positive in one is the same as a negative in the other.
Take each opposite pair to determine the rotation about both axes orthoganol to the line between their centers.
Example: East-West
If we look at the East to West pair, then the spin components are in the Y and Z dimensions.
We split this into 2 vectors per side, one for the Y and one for the Z.
Now we have 2 Y vectors and 2 Z vectors.
We subtract one vector from the other for each dimension.
Why do we subtract? Because that removes the directional component of these vectors. You can think of it as rotating one of the vectors around to the other side.
That gives us 1 Y vector and 1 Z vector for this pair.
Each vector represents a tangential velocity, so we use my Spin Velocity transform to convert those vectors into an angle about each axis.
We do that for each pair so we end up with 2 X angles, 2 Y angles and 2 Z angles.
Sum for each dimension to end up with a single angle for each.
We now have 3 rotations that we need to combine into 1.
To do that, we convert them into quaternions and multiply them all together (multiply is add for quaternions).
The resultant quaternion can then be multiplied with the existing spin component of the particle.
The linear velocity will need to be converted back into the working coordinate system. This should just involve applying the original orientation transform to the results. The spin component should not matter.
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
.
Overall looking good. A few questions prevent me from seeing the big picture just yet. I'm sure I'm making a bad assumption or two. Please provide additional clarification and/or corrections.
North and South poles are of course fixed by each particle’s spin axis. Selection of E,W,F, and B are somewhat arbitrary. How are they determined? We know they must all lie on the same equatorial plane, at right angle to the spin axis and through the center of the particle. Once known, the E,W,F,B positions must advance with the particle’s spin. I would assume they must all be tracked for all moments in time. Is that correct?
The proto world ‘system’ is comprised of n particles: a1, a2, …, an. Let’s start with a1. During calculations of its received charge, a1’s center becomes the center of the world system; the world system is also rotated to align with a1’s spin axis and E,W,F,B positions. All the charge density received by a1 (currently - this particle) from all the other particles are calculated for a single moment. Advancing the received charge density calculation through all the remaining charge receiving particles would show the world system is constantly rotating about each and every particle’s spin axis. That seems like a lot of rotating.
How are each particle’s charge emissions calculated? Emissions are a function of the particle’s latitude, or world system. I agree that a small differential due to the emitting particle’s spin will be felt on the receiving particle. Both emitting and receiving particles' linear and spin velocities through the world system must be taken into account.
.
Overall looking good. A few questions prevent me from seeing the big picture just yet. I'm sure I'm making a bad assumption or two. Please provide additional clarification and/or corrections.
North and South poles are of course fixed by each particle’s spin axis. Selection of E,W,F, and B are somewhat arbitrary. How are they determined? We know they must all lie on the same equatorial plane, at right angle to the spin axis and through the center of the particle. Once known, the E,W,F,B positions must advance with the particle’s spin. I would assume they must all be tracked for all moments in time. Is that correct?
The proto world ‘system’ is comprised of n particles: a1, a2, …, an. Let’s start with a1. During calculations of its received charge, a1’s center becomes the center of the world system; the world system is also rotated to align with a1’s spin axis and E,W,F,B positions. All the charge density received by a1 (currently - this particle) from all the other particles are calculated for a single moment. Advancing the received charge density calculation through all the remaining charge receiving particles would show the world system is constantly rotating about each and every particle’s spin axis. That seems like a lot of rotating.
How are each particle’s charge emissions calculated? Emissions are a function of the particle’s latitude, or world system. I agree that a small differential due to the emitting particle’s spin will be felt on the receiving particle. Both emitting and receiving particles' linear and spin velocities through the world system must be taken into account.
.
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
The N,S,E,W,F,B positions are not real positions in the world system. They are just calculation points in the math. We do not need to track them over time because they are just a way to determine the charge effects from different sides of the particle. I defined them to be set to the dimensions, not the particle, because I am using them to easily split the vectors.
By split the vectors, I mean to be able to extract their X, Y and Z components. For a given charge vector, the Y might be the linear velocity component and the X and Z are the spin components. This is determined by looking at which dimension points to the center of the particle and that will be the linear velocity dimension for that position.
With respect to what is considered the center, it actually varies during the calculations. For the algorithm described above, let's call it the Velocity algorithm (because it calculates velocity and spin), the current particle is considered center. However, for the Charge Density algorithm, the other particle is the center. This is just an artifact of the math. You could calculate it either way but I think it is easier if the source of the charge is center and the measurement point is relative to that.
The calculations are made, not for a moment, but for a time interval. I have not included any time math in that description but it will need to be handled. Essentially, time is handled by determining how much real time has passed since the last frame, looking at the units that you specify for things like velocity (m/s, km/h, etc) and converting them to the amount of time that has passed. So If we specified that a particle has a velocity of (0, 1, 0) which is defined as m/s, and the last frame was 1/60th of a second ago (60 frames per second), then the actual velocity to be used will be (0, 1/60, 0) per frame.
It is not the world system that is rotating, but each and every particle. It is possible that some will not have spin, of course. You have to find the right perspective to understand this stuff. The math above does perform a lot of rotations because it needs to arrange everything with respect to the current particle being calculated. That is just for the math though. It does not, in any way, actually rotate the particle. You will never see those rotations in the scene. You will see the rotations that are a result of the math, but not the rotations performed during the math.
When I say we want to orient a particle with respect to the current particle, it is just rotating the temporary copy of the position of that particle. Not the actual position of it. In fact, the positions and orientations used in these calculations are never written back to the particles. We read them in, but never write them back out because the result of these calculations are velocities and spins (1 each per particle). Velocity and spin are properties of the particle which are applied every frame. The application of those properties can happen at a different frequency than the calculations.
Suppose we find that these calculations are excruciatingly slow. If we were updating the position and orientation every time we calculate, then there is nothing we can do about it being slow. However, by disconnecting the calculation from the update, we can choose to calculate every 2nd frame, or 3rd, or what-ever. The velocities and spins are still applied every frame, but they themselves are not updated that often. This is one way to set the precision of the model.
I do have a rough outline of the Charge Density algorithm. It still needs work, and it is only an approximation, but it should be fairly good. The beauty of separating these 2 algorithms is that we can replace either one if we find a better way. I'll try to expand on the charge density algorithm and post it.
By split the vectors, I mean to be able to extract their X, Y and Z components. For a given charge vector, the Y might be the linear velocity component and the X and Z are the spin components. This is determined by looking at which dimension points to the center of the particle and that will be the linear velocity dimension for that position.
With respect to what is considered the center, it actually varies during the calculations. For the algorithm described above, let's call it the Velocity algorithm (because it calculates velocity and spin), the current particle is considered center. However, for the Charge Density algorithm, the other particle is the center. This is just an artifact of the math. You could calculate it either way but I think it is easier if the source of the charge is center and the measurement point is relative to that.
The calculations are made, not for a moment, but for a time interval. I have not included any time math in that description but it will need to be handled. Essentially, time is handled by determining how much real time has passed since the last frame, looking at the units that you specify for things like velocity (m/s, km/h, etc) and converting them to the amount of time that has passed. So If we specified that a particle has a velocity of (0, 1, 0) which is defined as m/s, and the last frame was 1/60th of a second ago (60 frames per second), then the actual velocity to be used will be (0, 1/60, 0) per frame.
It is not the world system that is rotating, but each and every particle. It is possible that some will not have spin, of course. You have to find the right perspective to understand this stuff. The math above does perform a lot of rotations because it needs to arrange everything with respect to the current particle being calculated. That is just for the math though. It does not, in any way, actually rotate the particle. You will never see those rotations in the scene. You will see the rotations that are a result of the math, but not the rotations performed during the math.
When I say we want to orient a particle with respect to the current particle, it is just rotating the temporary copy of the position of that particle. Not the actual position of it. In fact, the positions and orientations used in these calculations are never written back to the particles. We read them in, but never write them back out because the result of these calculations are velocities and spins (1 each per particle). Velocity and spin are properties of the particle which are applied every frame. The application of those properties can happen at a different frequency than the calculations.
Suppose we find that these calculations are excruciatingly slow. If we were updating the position and orientation every time we calculate, then there is nothing we can do about it being slow. However, by disconnecting the calculation from the update, we can choose to calculate every 2nd frame, or 3rd, or what-ever. The velocities and spins are still applied every frame, but they themselves are not updated that often. This is one way to set the precision of the model.
I do have a rough outline of the Charge Density algorithm. It still needs work, and it is only an approximation, but it should be fairly good. The beauty of separating these 2 algorithms is that we can replace either one if we find a better way. I'll try to expand on the charge density algorithm and post it.
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
Charge Density Algorithm
- Code:
// this array is used to approximate the charge density from equator to pole
// the values are percentages
// it is mirrored at the equator
// it handles the fact that the strongest emission is as 30° N/S, not at the equator itself
// the length of this array is arbitrary, you can include more values for more precision
CHARGE_DENSITY = [80, 90, 100, 90, 70 , 50, 30, 10, 5, 0];
// this value specifies the max distance from a particle that its charge field can be felt
// this is used for performance reasons
MAX_CHARGE_DISTANCE = ?
// this value is used to set the maximum amount of charge that a particle can emit
// it should be replaced by a 1/r^4 calculation at some stage
MAX_CHARGE_DENSITY = ?
// this value is used to specify the velocity applied by the max charge density
// this is a way to convert between a density and a velocity
MAX_CHARGE_STRENGTH = ?
// find vector to p2
v1 = p1 - p2
if( v1.length < p1Radius )
{
// collision of actual particles
return collision( p1, p2, ... );
}
// find distance as a factor of max charge distance
d = v1.length / MAX_CHARGE_DISTANCE;
if( d < 1 )
{
// find equator to pole ratio
v2 = [v1.x, 0, v1.z]
l2 = v2.length / MAX_CHARGE_DISTANCE;
y2 = v1.y / MAX_CHARGE_DISTANCE;
if( y2 == 0 )
{
// perfectly on the equator
epr = l2;
}
else
{
// somewhere between equator and pole, including perfectly at the pole
epr = l2 / abs( y2 )
}
// find the charge density
i = Integer.valueOf( epr * (CHARGE_DENSITY.length-1) );
epf = CHARGE_DENSITY[i] / 100.0;
df = d * MAX_CHARGE_DENSITY // TODO 1/r^4
v1.normalize();
v1.scale( d * epf * MAX_CHARGE_STRENGTH )
// TODO find resultant spin of the charge field, if we want to use that
}
else
{
// outside of effective radius
v1 = [0, 0, 0]; // = [0, 0, 0, 0] if using charge photon spin
}
return v1;
This one is a bit rougher than the last, but also closer to real code.
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
I have started to create a Javascript implementation of these algorithms. This will force me to look deeper at certain parts and get a better understanding of what data I have available at various stages. This will be the fallback implementation if shaders are not available on the running system. It does not use shaders at all, so I expect it to be a fair bit slower than the final form. However, I am designing it in such a way that it is shader friendly. I would do some things differently if I was not, but this will make it easier to port to the shader language or even OpenCL.
I can give you a better idea of how these functions look now. The Velocity algorithm is the driver. It is what the application must call to calculate the velocities and spins for all particles. The Velocity algorithm calls the Charge Density algorithm to perform its job. From the applications perspective, these algorithms use the position and orientation of all particles as read-only input, and the velocity and spin of all particles as write-only output. These 4 datasets are what we are going to transport through images (or textures) in the shader.
Each dataset is an array of floating point values. The values are grouped into a set number of items to form some larger entity. For example, the position array uses sets of 3 values to form a vector: X, Y, Z. The spin array uses 4 values to form a quaternion: X, Y, Z, W. When in texture form, each group of 3 or 4 values are called a texel or pixel. So the X, Y, Z(, W) are the same as R, G, B(, A) channels if it was real image data.
The function declaration for the Velocity algorithm might look like this:
It won't actually look like that in the shader, but it will equate to the same thing. It also doesn't look like that in my Javascript implementation but it does provide the data in the same way (as in 4 arrays) even though it is slower to do it like that in JS. An OpenCL implementation would look like that, but with some read-only and write-only flags added in.
Each item in these arrays, where an item is a group of 3 or 4 values, contains the data for a particular particle. The 1st item contains data for the 1st particle up to the Nth item for the Nth particle. To retrieve the correct data for a particular particle, you multiply its item index by the number of values in the item like this:
So if we wanted to get the 3rd items position, we would go to the 3*3 = 9th value and take 3 of them to form a vector. If we wanted the 3rd items orientation, then we go to 3*4 = 12th value and take 4 of them to form a quaternion. This is generally how you pass around large amounts of data to the GPU.
The Charge Density function only needs the position and orientation of the emitting particle, the position of the measurement point, and a vector to store the result. It will look like this:
I have just discovered that GLSL does not supply any support for quaternions, so I will have to code up their math, much like I have for matrices. Not a big deal, but I also might see if I can avoid the quaternion math as much as possible because they are expensive operations. It might be better to convert the quaternions into matrices. I'm not sure at this point.
I can give you a better idea of how these functions look now. The Velocity algorithm is the driver. It is what the application must call to calculate the velocities and spins for all particles. The Velocity algorithm calls the Charge Density algorithm to perform its job. From the applications perspective, these algorithms use the position and orientation of all particles as read-only input, and the velocity and spin of all particles as write-only output. These 4 datasets are what we are going to transport through images (or textures) in the shader.
Each dataset is an array of floating point values. The values are grouped into a set number of items to form some larger entity. For example, the position array uses sets of 3 values to form a vector: X, Y, Z. The spin array uses 4 values to form a quaternion: X, Y, Z, W. When in texture form, each group of 3 or 4 values are called a texel or pixel. So the X, Y, Z(, W) are the same as R, G, B(, A) channels if it was real image data.
The function declaration for the Velocity algorithm might look like this:
- Code:
void calcVelocityAndSpin(float[] positions, float[] orientations, float[] velocities, float[] spins);
It won't actually look like that in the shader, but it will equate to the same thing. It also doesn't look like that in my Javascript implementation but it does provide the data in the same way (as in 4 arrays) even though it is slower to do it like that in JS. An OpenCL implementation would look like that, but with some read-only and write-only flags added in.
Each item in these arrays, where an item is a group of 3 or 4 values, contains the data for a particular particle. The 1st item contains data for the 1st particle up to the Nth item for the Nth particle. To retrieve the correct data for a particular particle, you multiply its item index by the number of values in the item like this:
- Code:
int posIndex = itemIndex * 3;
int orientIndex = itemIndex * 4;
So if we wanted to get the 3rd items position, we would go to the 3*3 = 9th value and take 3 of them to form a vector. If we wanted the 3rd items orientation, then we go to 3*4 = 12th value and take 4 of them to form a quaternion. This is generally how you pass around large amounts of data to the GPU.
The Charge Density function only needs the position and orientation of the emitting particle, the position of the measurement point, and a vector to store the result. It will look like this:
- Code:
void calcChargeDensity(vec3 sourcePoint, vec4 sourceOrient, vec3 measurePoint, vec3* dst);
I have just discovered that GLSL does not supply any support for quaternions, so I will have to code up their math, much like I have for matrices. Not a big deal, but I also might see if I can avoid the quaternion math as much as possible because they are expensive operations. It might be better to convert the quaternions into matrices. I'm not sure at this point.
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
Nevyn wrote. I can give you a better idea of how these functions look now. The Velocity algorithm is the driver. It is what the application must call to calculate the velocities and spins for all particles. The Velocity algorithm calls the Charge Density algorithm to perform its job. From the applications perspective, these algorithms use the position and orientation of all particles as read-only input, and the velocity and spin of all particles as write-only output. These 4 datasets are what we are going to transport through images (or textures) in the shader.
Wow Nevyn, I love it when you talk data like that.
Thanks for the explanations. So it seems we will be building the Charged Particle Interaction Model (CPIM) from the existing Proto-Planet (aka webgl gpgpu debris) source after all. Currently CPIM has four shaders:
1. Fragment shader for position -->
2. Fragment shader for velocity -->
3. Particles vertex shader -->
4. Particles fragment shader -->
Makes perfect sense to add orientation to position; and spin to velocity. Spinning does add complexity.
CPIM includes one unusual Three.js source file. GPUComputationRenderer.js, author yomboprime https://github.com/yomboprime, https://github.com/yomboprime/GPGPU-threejs-demos. Did you happen to look at it? The author has four other related particle examples. I'm hoping it may have some bearing on your quaternion/matrix thinking.
.
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
I haven't looked at the existing shaders since you first mentioned this project, so I'm not sure how it will fit in, but I would expect it to be a new shader, not added to an existing one, or maybe added to the shader that contains the gravity math. We can't split the datasets that I have defined, they are all needed together in the same shader.
I'm not convinced that we need to use this example as the basis. We could create a new one from scratch, but there is nothing stopping us from doing so either. So I am happy to run with it for now. I do like the way it renders the spheres as glowing. I will probably attempt to add my charge shaders from AtomicViewer to that to show the equatorial emission.
I did see the GPUComputationRenderer and was pleased to do so. However, upon looking over it again, I'm not sure if I want to use it or not. It is a bit inefficient in its memory usage. Basically all textures are packed with 4 values per texel. Half of mine only need 3, so 1 byte is wasted per texel in those 2 datasets. That might not sound like much to worry about, but every little bit is worth worrying about at this level. That is 2 bytes per particle that will need to be written to GPU memory and copied back to main memory, 60 times a second, for no reason. However, I might get lazy and just go with it for convenience.
It won't help with quaternions or matrices though. That is all inside of the shader, so only GLSL can help with that and they don't have the routines available yet. The math isn't difficult, just expensive computationally. Lots of multiplications, and a multiply operation is about 9 times more expensive than an add operation at the processing level (CPU or GPU). However, converting quaternions into matrices can be almost as expensive so I need to make sure that it is worth the effort.
My first approach is usually to do it the way I see it and then optimize later. Once you have an algorithm working, it is easier to see how to change it.
I'm not convinced that we need to use this example as the basis. We could create a new one from scratch, but there is nothing stopping us from doing so either. So I am happy to run with it for now. I do like the way it renders the spheres as glowing. I will probably attempt to add my charge shaders from AtomicViewer to that to show the equatorial emission.
I did see the GPUComputationRenderer and was pleased to do so. However, upon looking over it again, I'm not sure if I want to use it or not. It is a bit inefficient in its memory usage. Basically all textures are packed with 4 values per texel. Half of mine only need 3, so 1 byte is wasted per texel in those 2 datasets. That might not sound like much to worry about, but every little bit is worth worrying about at this level. That is 2 bytes per particle that will need to be written to GPU memory and copied back to main memory, 60 times a second, for no reason. However, I might get lazy and just go with it for convenience.
It won't help with quaternions or matrices though. That is all inside of the shader, so only GLSL can help with that and they don't have the routines available yet. The math isn't difficult, just expensive computationally. Lots of multiplications, and a multiply operation is about 9 times more expensive than an add operation at the processing level (CPU or GPU). However, converting quaternions into matrices can be almost as expensive so I need to make sure that it is worth the effort.
My first approach is usually to do it the way I see it and then optimize later. Once you have an algorithm working, it is easier to see how to change it.
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
Since I am about to commit the Javascript implementation of these algorithms to GIT, I thought I might go over how I setup my JS files.
In Javascript, when you define a variable, it has some scope. If you are inside of a function, then that function is the scope. If you are inside of a code block (surrounded by { and }), then that block is the scope. If you are outside of any function, then it is in the global scope. The variable does not exist outside of that scope. You can not use it if you can't see it. If the variable is in the global scope, then you can use it anywhere. If it is in a function, then you can use it anywhere in that function. If it is in a code block, then you can only use it in that code block and not anywhere else, even in the function that contains the block.
Now, global variables all get put into the same place (they are actually stored as properties of the window object that is supplied by the browser). Because of this, you can get name collisions and not realise that you are actually effecting other code just because they both declare the same variable. I have spent days tracking down such bugs.
To get around this, I create my own module that contains all of the code for that module and keeps it in its own scope. You have already used such modules. THREE is the module for ThreeJS. That is why you have to specify THREE in front of any class that you use from it, such as THREE.Vector3. The module object itself is still stored in the global scope, so you can access it anywhere, but now anything within that module is kept separate from the global scope.
This could be as simple as declaring an object like this:
However, I take it a step further so that I can create a private space so that no other code can access certain parts of that module. To accomplish that I use a function. Javascript is a bit of a strange language and it has a feature called Closures. Closures are basically a hierarchy of scope. If you are inside of a function and use a variable that you have not declared in that function, then it will look at the scope that that function was declared in, if not found it will look at the scope of that scope, etc, etc. If it still hasn't found it, then it will look at the global variables.
Here's an example:
Now, those variables all have unique names so there is no problem. Let's look at another example where they all use the same name.
That is perfectly usable code. I don't recommend doing that as it is confusing and prone to errors, but it will work and all of those variables are unique and will not collide at all. But if we forgot to use the var declaration, then things get weird.
The first usage of variable will actually create it, even though it has no var declaration. All of the other uses will use that global variable though, so we are getting collisions. You can use this to your own advantage and I do so sometimes. What I want to show now though, is how to create a private space.
We accomplish that by creating our module inside of a function. Therefore, we can create variables in that function that are private to it. Any code in the module can access them, but nothing outside of that module can.
That is the outline, but it does not actually create any private variables. The module variable is actually private, but we are returning it from the function to make it accessible as a global variable called MyModule. So in other code we could use it like this: MyModule.myVar = 2.0; Locally though, we must refer to it as module because MyModule may not exist yet. You actually can use MyModule in some places, but it is best to use the module local variable because then we can easily change the name of the module without having to replace its usage inside of its own code.
The private scope is created by declaring the module inside of a function, but we also have to immediately execute that function. To do that, we just add the parameter declaration to the end of the function. This module does not take any parameters but if we wanted to use THREE, then we would pass it in to this function like this:
Notice that I had to add THREE to the argument list in the function declaration (at the top) and also in the parameter list to call the function (at the bottom). We could actually rename THREE at this point if we wanted to. It would only be renamed within this function.
I don't recommend doing that though, unless you absolutely have to.
The whole function and call declaration is wrapped in ( and ) just to make sure that it is executed.
Note that myVector is a private variable and can not be accessed from anywhere outside of this module. This can be very handy since that variable will exist for the life of the application. We can create objects and then use them within the functions and classes exposed by the module. They act like static variables in other languages. We might use them as constants, but they are actually variables so you can change their values if you want to.
I am getting a bit too advanced here, but I just want you to be able to recognize the structure and have at least some notion of why it is being used.
In Javascript, when you define a variable, it has some scope. If you are inside of a function, then that function is the scope. If you are inside of a code block (surrounded by { and }), then that block is the scope. If you are outside of any function, then it is in the global scope. The variable does not exist outside of that scope. You can not use it if you can't see it. If the variable is in the global scope, then you can use it anywhere. If it is in a function, then you can use it anywhere in that function. If it is in a code block, then you can only use it in that code block and not anywhere else, even in the function that contains the block.
Now, global variables all get put into the same place (they are actually stored as properties of the window object that is supplied by the browser). Because of this, you can get name collisions and not realise that you are actually effecting other code just because they both declare the same variable. I have spent days tracking down such bugs.
To get around this, I create my own module that contains all of the code for that module and keeps it in its own scope. You have already used such modules. THREE is the module for ThreeJS. That is why you have to specify THREE in front of any class that you use from it, such as THREE.Vector3. The module object itself is still stored in the global scope, so you can access it anywhere, but now anything within that module is kept separate from the global scope.
This could be as simple as declaring an object like this:
- Code:
var MyModule = {
myVar: 1.0,
myOtherVar: 'is a string'
};
However, I take it a step further so that I can create a private space so that no other code can access certain parts of that module. To accomplish that I use a function. Javascript is a bit of a strange language and it has a feature called Closures. Closures are basically a hierarchy of scope. If you are inside of a function and use a variable that you have not declared in that function, then it will look at the scope that that function was declared in, if not found it will look at the scope of that scope, etc, etc. If it still hasn't found it, then it will look at the global variables.
Here's an example:
- Code:
var globalVariable = 1.0;
function myFunction()
{
var functionVariable = 2.0;
if( someCondition )
{
var blockVariable = 3.0;
}
// note that we do not need an if, or while, or any control structure to create a block
{
var anotherBlockVariable = 4.0;
}
}
Now, those variables all have unique names so there is no problem. Let's look at another example where they all use the same name.
- Code:
var variable = 1.0;
function myFunction()
{
var variable = 2.0;
if( someCondition )
{
var variable = 3.0;
}
// note that we do not need an if, or while, or any control structure to create a block
{
var variable = 4.0;
}
}
That is perfectly usable code. I don't recommend doing that as it is confusing and prone to errors, but it will work and all of those variables are unique and will not collide at all. But if we forgot to use the var declaration, then things get weird.
- Code:
variable = 1.0;
function myFunction()
{
variable = 2.0;
if( someCondition )
{
variable = 3.0;
}
// note that we do not need an if, or while, or any control structure to create a block
{
variable = 4.0;
}
}
The first usage of variable will actually create it, even though it has no var declaration. All of the other uses will use that global variable though, so we are getting collisions. You can use this to your own advantage and I do so sometimes. What I want to show now though, is how to create a private space.
We accomplish that by creating our module inside of a function. Therefore, we can create variables in that function that are private to it. Any code in the module can access them, but nothing outside of that module can.
- Code:
var MyModule = (function()
{
var module = {
myVar: 1.0,
myOtherVar: 'is a string'
};
return module;
}());
That is the outline, but it does not actually create any private variables. The module variable is actually private, but we are returning it from the function to make it accessible as a global variable called MyModule. So in other code we could use it like this: MyModule.myVar = 2.0; Locally though, we must refer to it as module because MyModule may not exist yet. You actually can use MyModule in some places, but it is best to use the module local variable because then we can easily change the name of the module without having to replace its usage inside of its own code.
The private scope is created by declaring the module inside of a function, but we also have to immediately execute that function. To do that, we just add the parameter declaration to the end of the function. This module does not take any parameters but if we wanted to use THREE, then we would pass it in to this function like this:
- Code:
var MyModule = (function( THREE )
{
var module = {
myVar: 1.0,
myOtherVar: 'is a string'
};
return module;
}( THREE ));
Notice that I had to add THREE to the argument list in the function declaration (at the top) and also in the parameter list to call the function (at the bottom). We could actually rename THREE at this point if we wanted to. It would only be renamed within this function.
- Code:
var MyModule = (function( FOUR )
{
var module = {
myVar: 1.0,
myOtherVar: 'is a string'
};
var myVector = new FOUR.Vector3();
return module;
}( THREE ));
I don't recommend doing that though, unless you absolutely have to.
The whole function and call declaration is wrapped in ( and ) just to make sure that it is executed.
Note that myVector is a private variable and can not be accessed from anywhere outside of this module. This can be very handy since that variable will exist for the life of the application. We can create objects and then use them within the functions and classes exposed by the module. They act like static variables in other languages. We might use them as constants, but they are actually variables so you can change their values if you want to.
I am getting a bit too advanced here, but I just want you to be able to recognize the structure and have at least some notion of why it is being used.
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
I should probably talk a bit about Javascript Classes as well. The first thing you need to know is that JS does not have classes. The second thing you need to know is that I use classes in JS a lot.
Confused yet?
Javascript is what is called a Prototyping Language. It doesn't have strict requirements on what any object can store within itself. You can even add and remove them as you go. In a language like Java, you define what a class can store and it will only ever store that data and you can not remove it. You can set it to null, so it has no value, but the variable itself will always exist on every object of that class.
So how do we use classes in JS? Well, JS uses prototypes to accomplish the same thing (with differences). You declare a function, and then attach a prototype to that function and the prototype becomes an extension of that function. To use the function as a class, you just use the new keyword to create an instance. e.g. var myVector = new THREE.Vector3();
THREE.Vector3 is actually a function and it has a prototype and that prototype contains all of the functions, which we now call methods, for that class. There is only 1 prototype, but every new object from that class contains a reference to it and can use the shared data and methods in it.
Let's look at an example for some clarity:
We could then use it like this, assuming it was declared in a module called MyModule:
So what's the big deal? Well, it is more efficient than the alternative and we can set up class hierarchies by extending one class with another.
Firstly, the old way, before prototypes were added to JS:
While it is quite a bit less code to write, the problem is that every object created by this function will create its own function called getName. If you create 1000 instances of MyClass, then there will be 1000 instances of the getName function. However, with a prototype, there is only 1 instance of the getName function and all 1000 objects use it. This is much better on memory usage and much faster to execute because we don't have to create 999 functions that all do the same thing.
We can also create sub-classes. This allows you to extend one class with another. You do this by supplying the prototype of the class you want to extend when you create the prototype of the class that is extending.
We can override methods of the parent class in this child. Instances of the parent class still use its own version of the method, but instances of the child class use their own version. Any methods not overridden are still available in the sub-class.
Again, it is not too important to be able to use this stuff, but you will need to recognize it to understand my code.
Confused yet?
Javascript is what is called a Prototyping Language. It doesn't have strict requirements on what any object can store within itself. You can even add and remove them as you go. In a language like Java, you define what a class can store and it will only ever store that data and you can not remove it. You can set it to null, so it has no value, but the variable itself will always exist on every object of that class.
So how do we use classes in JS? Well, JS uses prototypes to accomplish the same thing (with differences). You declare a function, and then attach a prototype to that function and the prototype becomes an extension of that function. To use the function as a class, you just use the new keyword to create an instance. e.g. var myVector = new THREE.Vector3();
THREE.Vector3 is actually a function and it has a prototype and that prototype contains all of the functions, which we now call methods, for that class. There is only 1 prototype, but every new object from that class contains a reference to it and can use the shared data and methods in it.
Let's look at an example for some clarity:
- Code:
...
module.MyClass = function( name )
{
this.name = name;
};
module.MyClass.prototype = Object.create( {} );
module.MyClass.prototype.getName = function()
{
return this.name;
};
...
We could then use it like this, assuming it was declared in a module called MyModule:
- Code:
var cls = new MyModule.MyClass( 'Nevyn' );
var name = cls.getName();
// of course, we can also access the name field directly like this:
name = cls.name;
// but I wanted to show classes, not field access
So what's the big deal? Well, it is more efficient than the alternative and we can set up class hierarchies by extending one class with another.
Firstly, the old way, before prototypes were added to JS:
- Code:
...
module.MyClass = function( name )
{
this.name = name;
this.getName = function()
{
return this.name;
};
};
...
While it is quite a bit less code to write, the problem is that every object created by this function will create its own function called getName. If you create 1000 instances of MyClass, then there will be 1000 instances of the getName function. However, with a prototype, there is only 1 instance of the getName function and all 1000 objects use it. This is much better on memory usage and much faster to execute because we don't have to create 999 functions that all do the same thing.
We can also create sub-classes. This allows you to extend one class with another. You do this by supplying the prototype of the class you want to extend when you create the prototype of the class that is extending.
- Code:
...
module.MySubClass = function( firstName, lastName )
{
module.MyClass.call( this, firstName );
this.lastName = lastName;
};
module.MySubClass.prototype = Object.create( module.MyClass.prototype );
module.MySubClass.prototype.getName = function()
{
return this.name + ' ' + this.lastName;
};
...
We can override methods of the parent class in this child. Instances of the parent class still use its own version of the method, but instances of the child class use their own version. Any methods not overridden are still available in the sub-class.
Again, it is not too important to be able to use this stuff, but you will need to recognize it to understand my code.
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
I'm getting worried about you, Airman! It's been a few days since I pushed my code to GIT, and I haven't heard from you. Are you still OK?
By the way, I had a look at the existing code and found a few things that I had not thought about. This will change the way the code is called and I still need to figure out exactly what the BufferGeometry object is going to store. It has to have something in it, but I don't really need it.
I am thinking that I will create another app along side this one for testing my implementation. I don't think this example is going to work for us but I will revisit that at a later date. I still need to get a good understanding of how to fit it into a shader, so my perception may change as I figure that out.
The way I setup my code, without looking at the existing code, expected a list of Object3D instances where each one is a sphere, for example. The actual visual representation is irrelevant, but the fact that it is its own Object3D is critical. I then take the position and orientation from each one, encode it into a data structure (array for me, texture for you), and send it to the code to calculate the velocities and spins of all particles, decode the data structure and write the velocity and spin back to each particle.
The existing code works differently, as it puts all of the positions into the BufferGeometry and operates on them in the shader. This will not work for me, as I want data to come back out of the shader, not just to change the position passed in to it.
The other problem I found is that when you add the data as a shader Attribute, you don't get to see all of the values for all of the other particles in the shader. You just see the value for the current vertex being processed. This is very different from OpenCL, where you get arrays which contain all data for all vertices, and have to find the correct data for the vertex being processed. So I need to change the way I think about this (which has been very OpenCL centric so far).
By the way, I had a look at the existing code and found a few things that I had not thought about. This will change the way the code is called and I still need to figure out exactly what the BufferGeometry object is going to store. It has to have something in it, but I don't really need it.
I am thinking that I will create another app along side this one for testing my implementation. I don't think this example is going to work for us but I will revisit that at a later date. I still need to get a good understanding of how to fit it into a shader, so my perception may change as I figure that out.
The way I setup my code, without looking at the existing code, expected a list of Object3D instances where each one is a sphere, for example. The actual visual representation is irrelevant, but the fact that it is its own Object3D is critical. I then take the position and orientation from each one, encode it into a data structure (array for me, texture for you), and send it to the code to calculate the velocities and spins of all particles, decode the data structure and write the velocity and spin back to each particle.
The existing code works differently, as it puts all of the positions into the BufferGeometry and operates on them in the shader. This will not work for me, as I want data to come back out of the shader, not just to change the position passed in to it.
The other problem I found is that when you add the data as a shader Attribute, you don't get to see all of the values for all of the other particles in the shader. You just see the value for the current vertex being processed. This is very different from OpenCL, where you get arrays which contain all data for all vertices, and have to find the correct data for the vertex being processed. So I need to change the way I think about this (which has been very OpenCL centric so far).
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
Hey Nevyn, thanks for asking, I'm fine. I was getting worried about you. I was occupied with the Book of Shaders tutorial. Silly me, I assumed bitbucket would send me an e-mail message when you changed CPIM.I'm getting worried about you, Airman! It's been a few days since I pushed my code to GIT, and I haven't heard from you. Are you still OK?
Ok, I did a pull. I'll be re-reading, trying to catch up.
.
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
I wasn't sure that it wouldn't send you that email. I don't get them at work when others push to the same project, but I do get them when you push to this one. Maybe it is because I am the owner of the project and have given you write access to it.
Please note that there isn't really anything for you to do at the moment. Just try to understand what I have done so far, but remember that it is not for shaders, so some things will be different than the tutorials you are looking through. I tried to make sure that I added comments to explain various parts, but if any are confusing then just ask.
Please note that there isn't really anything for you to do at the moment. Just try to understand what I have done so far, but remember that it is not for shaders, so some things will be different than the tutorials you are looking through. I tried to make sure that I added comments to explain various parts, but if any are confusing then just ask.
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
///\\\///\\\///\\\///\\\///\\\///\\\Charge Density Model
Given a particle, determine the charge field effects of other particles on it.
Conditions and setup:
Each particle is treated as if it was in a set orientation such that its North pole is +Y, East is +X and Front is +Z.
We want all calculations to be performed in this orientation so that we can split some vectors easily.
We will need to transform all other particles into this virtual coordinate system.
We do that by taking the orientation transform of this particle, inverting it, and applying to each other particle.
This will not actually change those particles, but will change the values in the temporary data we have for them.
Algorithm:
Code:
Calculate sum of charge densities from other particles at the cardinal positions on this particle (N,S,E,W,F,B).
For each position:
Split charge vector into 3 components: 1 linear velocity component that points to the center of the particle; 2 spin components that point in the other 2 dimensions.
The actual dimensions used are different for each position:
North: V=-Y, S=X,Z
South: V=+Y, S=X,Z
East: V=-X, S=Y,Z
West: V=+X, S=Y,Z
Front: V=+Z, S=X,Y
Back: V=-Z, S=X,Y
Where a vector with the same sign as the linear velocity dimension means a repulsion and the opposite means attraction (or do we ignore attraction and just let the other side apply repulsion?).
The spin components work in both directions and just changes the angle from positive to negative.
// Sorry Nevyn, I’m hung up. I either don’t agree or don't understand the “calculating sum of charge
// densities” algorithm above. I bolded two spots which I’ll cover in detail below. For the time being
// I guess it's probably better to discuss this here rather than through pushes and pulls, a future work
// routine. Please tell me where I'm going wrong.
We want all calculations to be performed in this orientation so that we can split some vectors easily.
// For the “charged density received” calculation we have at least two particles:
// 1. a single charge receiving particle which we will fix with 6 cardinal locations; and
// 2. n-1, all other remaining particles will be charge emitters. Unless I’m mistaken, I believe
// all “charge density received” calculations described are performed with the receiving particle
// in a single fixed orientation so that all incoming charge from all other particles present will be
// summed at the same six cardinal points simultaneously. On 10 July above you included a
// charge emission function. How is that function used in this algorithm?
///\\\///\\\///\\\///\\\///\\\///\\\
The actual dimensions used are different for each position:
North: V=-Y, S=X,Z
South: V=+Y, S=X,Z
East: V=-X, S=Y,Z
West: V=+X, S=Y,Z
Front: V=+Z, S=X,Y
Back: V=-Z, S=X,Y
// How can V = +/-X, +/-Y, or +/-Z?
// Each set of “charge density received” computations begin by “fixing into position” the
// receiving particle’s cardinal positions, which must be in accordance with the receiving
// particle’s spin axis. The direction of V is determined by the direction from the center of
// the emitting particle to the location of charge received (at the cardinal position).
// I believe those directional lines for one emitter and one receiver can be found by:
// 1. (RN-EC)X + (RN-EC)Y + (RN-EC)Z.
// 2. (RS-EC)X + (RS-EC)Y + (RS-EC)Z.
// 3. (RE-EC)X + (RE-EC)Y + (RE-EC)Z.
// 4. (RW-EC)X + (RW-EC)Y + (RW-EC)Z.
// 5. (RF-EC)X + (RF-EC)Y + (RF-EC)Z.
// 6. (RB-EC)X + (RB-EC)Y + (RB-EC)Z.
// For example, RN means the receiving particle’s North position. EC is the charge
// emitting particle's center.
// Note, none of those lines are parallel, they diverge. When the emitter and receiving
// particles are close together the V directions to the opposite cardinal location pairs,
// N-S, E-W, or F-B emission lines approach right angles. The further apart the two
// particles are separated, the more parallel the six lines become. This doesn't seem
// to be the same as you've described it.
// What do you think?
.
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
We definitely do not want to use GIT for discussions. GIT is for source code and source code only.
The charge emission function is used to calculate the charge emission of 1 particle upon 1 other particle, or at least some point that we define. It is used in this algorithm to calculate the charge effects from all other particles, from the 6 cardinal positions. Therefore, each other particle is measured 6 times for that 1 particle.
The directional lines can easily be found without re-orienting the particles, but what you can't do so easily is split the vectors up into linear velocity and spin components. If we did not re-orient, then we would have to rotate all of the vectors (or use sin and cos which is the same thing) in order to split them which amounts to a lot more math and hence, a lot more time to compute. I am already doing more computations than I need to by re-orienting within the charge emission function. I will more-than-likely change that to perform all re-orientations in the other algorithm and pass in the already oriented particle. That way, I only need to re-orient once per other particle per emission receiver. I'll look into that when I have it working (or close to it).
I'm not sure if that covers your problems or not. This is not a simple algorithm, so please keep asking until we both understand.
The charge emission function is used to calculate the charge emission of 1 particle upon 1 other particle, or at least some point that we define. It is used in this algorithm to calculate the charge effects from all other particles, from the 6 cardinal positions. Therefore, each other particle is measured 6 times for that 1 particle.
The directional lines can easily be found without re-orienting the particles, but what you can't do so easily is split the vectors up into linear velocity and spin components. If we did not re-orient, then we would have to rotate all of the vectors (or use sin and cos which is the same thing) in order to split them which amounts to a lot more math and hence, a lot more time to compute. I am already doing more computations than I need to by re-orienting within the charge emission function. I will more-than-likely change that to perform all re-orientations in the other algorithm and pass in the already oriented particle. That way, I only need to re-orient once per other particle per emission receiver. I'll look into that when I have it working (or close to it).
I'm not sure if that covers your problems or not. This is not a simple algorithm, so please keep asking until we both understand.
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
To give you an idea of why I am splitting vectors, you can look at the math for the trajectory of a ball thrown horizontally and vertically, say at 45°. You split the vector into the horizontal and vertical components so that you can apply gravity to the vertical component without touching the horizontal. I am doing a similar thing by saying that the vector from the cardinal point to the center of the particle (of that cardinal point, not the emitter) represents the linear velocity and the other 2 dimensions represent spin or I should say tangential velocity. Since the cardinal points are in different directions from the center, they each have a different direction for the linear velocity component. Even when 2 sides use the same dimension, they differ in whether positive is repulsion or attraction.
With respect to summing the charge vectors at each cardinal point, we are trying to find the net charge influence from that point upon the particle, so we must sum them. I do have reservations about the relative position of the measurement point because we should be ignoring emitters on the other side of the particle. I have thought about it and will implement it because those forces are already handled by the cardinal point on that side. I just have larger issues to think about before that, so please remind me if I forget. That's why I put a comment in my notes about ignoring attractions.
With respect to summing the charge vectors at each cardinal point, we are trying to find the net charge influence from that point upon the particle, so we must sum them. I do have reservations about the relative position of the measurement point because we should be ignoring emitters on the other side of the particle. I have thought about it and will implement it because those forces are already handled by the cardinal point on that side. I just have larger issues to think about before that, so please remind me if I forget. That's why I put a comment in my notes about ignoring attractions.
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
Airman wrote:I believe all “charge density received” calculations described are performed with the receiving particle in a single fixed orientation so that all incoming charge from all other particles present will be summed at the same six cardinal points simultaneously.
Well that is an interesting sentence because it is full of correct and yet wrong.
Both parts of that sentence are correct, but one does not lead to the other.
Airman wrote:all “charge density received” calculations described are performed with the receiving particle in a single fixed orientation
is correct, and
Airman wrote:all incoming charge from all other particles present will be summed at the same six cardinal points simultaneously
is correct, but...
You can't join them together because they are unrelated to each other. We use the fixed orientation to split the vectors. Summing the charge would be both required, and the same math, even if we calculated the charge some other way.
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
.
Given my full of correct - yet wrong statements, I'll try again.

Here is my understanding of a single iteration of the calculating sum of charge densities algorithm. The algorithm sums the amount of charge received by one of the charged particles (cyan) from all the other charge emitting particles (yellow) present. The three frames show the charge density received at the receiving particle’s cardinal positions from each of the three emitting particles. Note that the receiving particle is fixed in space – its orientation will remain the same as shown during this algorithm iteration. Each line - drawn from the center of the emitting particles to each of the cardinal positions of the receiving particle - shows the linear direction of charge emission, V; we do not see the two orthogonal spin components also present at each cardinal position.
Is that correct? Or does the algorithm reorient the receiver’s cardinal points for each emitting particle?
.
Given my full of correct - yet wrong statements, I'll try again.

Here is my understanding of a single iteration of the calculating sum of charge densities algorithm. The algorithm sums the amount of charge received by one of the charged particles (cyan) from all the other charge emitting particles (yellow) present. The three frames show the charge density received at the receiving particle’s cardinal positions from each of the three emitting particles. Note that the receiving particle is fixed in space – its orientation will remain the same as shown during this algorithm iteration. Each line - drawn from the center of the emitting particles to each of the cardinal positions of the receiving particle - shows the linear direction of charge emission, V; we do not see the two orthogonal spin components also present at each cardinal position.
Is that correct? Or does the algorithm reorient the receiver’s cardinal points for each emitting particle?
.
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
That shows the lines connecting the emission point to the cardinal points. But it does not show the velocity vectors. The velocity vectors are along the same direction as those lines, but are based at the cardinal point. This is because the vectors are a representation of the force applied at that cardinal point, from the other particle. Therefore, each velocity vector (or charge vector as I have called them before) starts at its cardinal point and points away from the center of the emitting particle with a length proportional to the force applied.
Take your center image above and I will number the lines 1 to 6 from top to bottom of the image so the order will be magenta, green, magenta, blue, green, magenta (is it meant to be red?). They all come from the same emission point but you can see that the force applied by line 3, the middle line, is almost completely linear velocity. However, lines 1 and 6 are almost completely tangential velocity, which will cause spin (in most cases but not if the charge is even on both sides, as they will cancel each other out and actually provide linear velocity).
So my algorithm measures those charge vectors for all other particles and stacks them together at those cardinal points. Then they are all added together to find the net charge influence at that point. That vector is then split into linear velocity and tangential velocity components.
Re-orienting Particles
The point of re-orienting particles is so that we can treat the receiver particle as if it was in a known orientation. That is, as if it did not actually have any orientation of its own. It is all about the receiver, not any of the other particles. However, it is the other particles that we have to re-orient because the orientation does not effect the location of the receiver particle, because the orientation is applied from the location of the receiver. It is effectively at (0, 0, 0). It does effect all other particle locations though, because they are definitely not at (0, 0, 0) with respect to the receiver particle. It is equivalent to taking your images above and rotating them with the cyan particle at the center of rotation.
It is basically saying 'I am the receiver and I am the center of everything and I define what is up and what is down.'. It puts everything else into the receivers local coordinate system or frame of reference, if you want to call it that.
While it does show the direction of charge emission being measured, that direction already contains both the linear and tangential components. You are thinking about a head-on collision but that is not what I am trying to accomplish. At times, there will be head-on collisions, which just means that all force is being applied along the linear velocity dimension for that cardinal point. The other 2 dimensions will be 0.
Let me paint a picture. I'd love to create it but it would take me too long. I need a vector scratch pad app.
We have a receiving particle at (0, 0, 0) with a radius of 1 and it has no orientation values so its north pole is at (0, 1, 0). The cardinal points are located here:
N: (0, 1, 0)
S: (0, -1, 0)
E: (1, 0, 0)
W: (-1, 0, 0)
F: (0, 0, 1)
B: (0, 0, -1)
Suppose we have an emitter particle at (5, 0, 0) and it also has no orientation so they are equator to equator.
From the East cardinal point we are going to get all charge along the X dimension. That is the linear velocity dimension for the East position so it is all linear velocity. The Y and Z components of the charge vector will be 0.
Suppose we have another emitter at (1, 5, 0) and it does have an orientation that rotates it 90° about the Z axis, which means that it is emitting down straight at the East position of the receiver.
From the East point, all charge will be along the Y axis and none along the X or Z. You can clearly see that this is a tangential velocity and must cause spin, not linear motion.
Suppose we had yet another emitter that was at (5, 4, 0) and oriented so that it also emits straight at the East cardinal point of the receiver, which would be at a 45° angle.
From the East position, half of the charge vector will be along the X axis and half will be along the Y axis (none on the Z) so we have both linear velocity and tangential velocity in the same charge vector.
That is why I want to split them and that is why I want them oriented along the axes. I can just grab a single value (from whichever dimension I care about at the time) instead of extracting the angles from absolute positions which would involve all 3 values in a calculation for a single dimension.
There is method to my madness!
Take your center image above and I will number the lines 1 to 6 from top to bottom of the image so the order will be magenta, green, magenta, blue, green, magenta (is it meant to be red?). They all come from the same emission point but you can see that the force applied by line 3, the middle line, is almost completely linear velocity. However, lines 1 and 6 are almost completely tangential velocity, which will cause spin (in most cases but not if the charge is even on both sides, as they will cancel each other out and actually provide linear velocity).
So my algorithm measures those charge vectors for all other particles and stacks them together at those cardinal points. Then they are all added together to find the net charge influence at that point. That vector is then split into linear velocity and tangential velocity components.
Re-orienting Particles
The point of re-orienting particles is so that we can treat the receiver particle as if it was in a known orientation. That is, as if it did not actually have any orientation of its own. It is all about the receiver, not any of the other particles. However, it is the other particles that we have to re-orient because the orientation does not effect the location of the receiver particle, because the orientation is applied from the location of the receiver. It is effectively at (0, 0, 0). It does effect all other particle locations though, because they are definitely not at (0, 0, 0) with respect to the receiver particle. It is equivalent to taking your images above and rotating them with the cyan particle at the center of rotation.
It is basically saying 'I am the receiver and I am the center of everything and I define what is up and what is down.'. It puts everything else into the receivers local coordinate system or frame of reference, if you want to call it that.
Airman wrote:Each line - drawn from the center of the emitting particles to each of the cardinal positions of the receiving particle - shows the linear direction of charge emission, V; we do not see the two orthogonal spin components also present at each cardinal position.
While it does show the direction of charge emission being measured, that direction already contains both the linear and tangential components. You are thinking about a head-on collision but that is not what I am trying to accomplish. At times, there will be head-on collisions, which just means that all force is being applied along the linear velocity dimension for that cardinal point. The other 2 dimensions will be 0.
Let me paint a picture. I'd love to create it but it would take me too long. I need a vector scratch pad app.
We have a receiving particle at (0, 0, 0) with a radius of 1 and it has no orientation values so its north pole is at (0, 1, 0). The cardinal points are located here:
N: (0, 1, 0)
S: (0, -1, 0)
E: (1, 0, 0)
W: (-1, 0, 0)
F: (0, 0, 1)
B: (0, 0, -1)
Suppose we have an emitter particle at (5, 0, 0) and it also has no orientation so they are equator to equator.
From the East cardinal point we are going to get all charge along the X dimension. That is the linear velocity dimension for the East position so it is all linear velocity. The Y and Z components of the charge vector will be 0.
Suppose we have another emitter at (1, 5, 0) and it does have an orientation that rotates it 90° about the Z axis, which means that it is emitting down straight at the East position of the receiver.
From the East point, all charge will be along the Y axis and none along the X or Z. You can clearly see that this is a tangential velocity and must cause spin, not linear motion.
Suppose we had yet another emitter that was at (5, 4, 0) and oriented so that it also emits straight at the East cardinal point of the receiver, which would be at a 45° angle.
From the East position, half of the charge vector will be along the X axis and half will be along the Y axis (none on the Z) so we have both linear velocity and tangential velocity in the same charge vector.
That is why I want to split them and that is why I want them oriented along the axes. I can just grab a single value (from whichever dimension I care about at the time) instead of extracting the angles from absolute positions which would involve all 3 values in a calculation for a single dimension.
There is method to my madness!
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
Let's look at the charge vectors from above to see the larger algorithm.
R = receiver
E1 = emitter at (5, 0, 0)
E2 = emitter at (1, 4, 0), I changed this one a little bit
E3 = emitter at (5, 4, 0)
Relative to the East cardinal point each emitter is at:
E1 = (4, 0, 0);
E2 = (0, 4, 0);
E3 = (4, 4, 0).
The distance from East position to each one is:
E1 = 4
E2 = 4
E3 = sqrt( 4*4 + 4*4 ) = 5.65
Therefore the E1 and E2 particles have equal influence, but in different dimensions and E3 has a slightly smaller influence in both dimensions that E1 and E2 have.
For the sake of simplicity, let's just make the charge vector length equal to: 10 - distance. This is not how it would be in the real algorithm, but it doesn't really matter for this example.
The charge vectors would then have the following lengths:
E1 = 6
E2 = 6
E3 = 4.35
I just needed to get E3 as a smaller value than the others.
The charge vectors would be:
E1 = (-6, 0, 0)
E2 = (0, -6, 0)
E3 = (-3.07, -3.07, 0)
We sum these vectors to find the net charge vector.
(-6, 0, 0)
+ (0, -6, 0)
+ (-3.07, -3.07, 0)
= (-9.07, -9.07, 0)
For the East cardinal point, the linear velocity is in the -X dimension, so we take the X value: -9.07; as the linear velocity and put it into its own vector:
V = (-9.07, 0, 0).
The spin components are in the Y and Z dimensions so we take them and put them into their own vectors:
SY = (0, -9.07, 0),
SZ = (0, 0, 0).
At this stage, we need to merge all of the cardinal points together into a single linear velocity and a single tangential velocity which becomes the new velocity and spin for the receiver.
R = receiver
E1 = emitter at (5, 0, 0)
E2 = emitter at (1, 4, 0), I changed this one a little bit
E3 = emitter at (5, 4, 0)
Relative to the East cardinal point each emitter is at:
E1 = (4, 0, 0);
E2 = (0, 4, 0);
E3 = (4, 4, 0).
The distance from East position to each one is:
E1 = 4
E2 = 4
E3 = sqrt( 4*4 + 4*4 ) = 5.65
Therefore the E1 and E2 particles have equal influence, but in different dimensions and E3 has a slightly smaller influence in both dimensions that E1 and E2 have.
For the sake of simplicity, let's just make the charge vector length equal to: 10 - distance. This is not how it would be in the real algorithm, but it doesn't really matter for this example.
The charge vectors would then have the following lengths:
E1 = 6
E2 = 6
E3 = 4.35
I just needed to get E3 as a smaller value than the others.
The charge vectors would be:
E1 = (-6, 0, 0)
E2 = (0, -6, 0)
E3 = (-3.07, -3.07, 0)
We sum these vectors to find the net charge vector.
(-6, 0, 0)
+ (0, -6, 0)
+ (-3.07, -3.07, 0)
= (-9.07, -9.07, 0)
For the East cardinal point, the linear velocity is in the -X dimension, so we take the X value: -9.07; as the linear velocity and put it into its own vector:
V = (-9.07, 0, 0).
The spin components are in the Y and Z dimensions so we take them and put them into their own vectors:
SY = (0, -9.07, 0),
SZ = (0, 0, 0).
At this stage, we need to merge all of the cardinal points together into a single linear velocity and a single tangential velocity which becomes the new velocity and spin for the receiver.
Last edited by Nevyn on Wed Jul 18, 2018 4:28 pm; edited 1 time in total
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
.
Thanks Nevyn, I think I've got it. I was still thinking of head-on collisions. Are all your ideas so difficult?
I think pictures are essential - for me anyway. I’m more than happy to provide diagrams. I may even overdo it. Please feel free to reject, mark-up, change or make diagram requests.
The following simple examples make perfect sense, including your previous text as explanation. As with my previous diagram, I show the emission/CardinalPosition (CP) directional lines only. I would need to zoom in to show the V components at each cardinal position. All particles lie in the z=0 plane. Note that my Cad system UCS Y and Z axis colors are opposite to the CP coloring choices I used here.

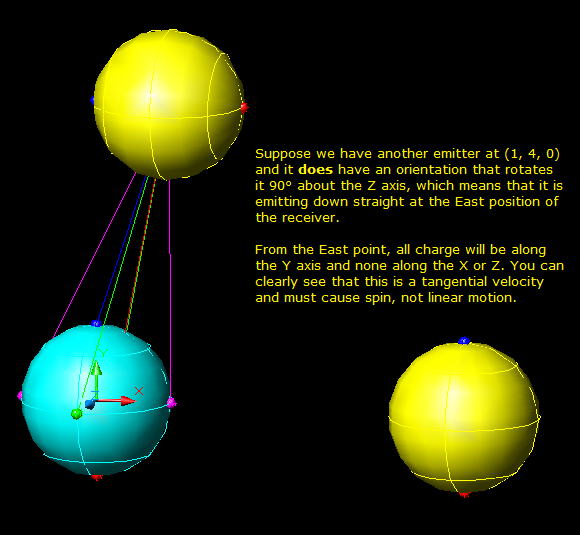

///////////////////////////////////////////////
Everyone, anyone, please feel free to add ideas.
///////////////////////////////////////////////
P.S. Corrected diagrams to agree with particle position change from (1,5,0) to (1,4,0)
.
Thanks Nevyn, I think I've got it. I was still thinking of head-on collisions. Are all your ideas so difficult?
I think pictures are essential - for me anyway. I’m more than happy to provide diagrams. I may even overdo it. Please feel free to reject, mark-up, change or make diagram requests.
The following simple examples make perfect sense, including your previous text as explanation. As with my previous diagram, I show the emission/CardinalPosition (CP) directional lines only. I would need to zoom in to show the V components at each cardinal position. All particles lie in the z=0 plane. Note that my Cad system UCS Y and Z axis colors are opposite to the CP coloring choices I used here.



///////////////////////////////////////////////
Everyone, anyone, please feel free to add ideas.
///////////////////////////////////////////////
P.S. Corrected diagrams to agree with particle position change from (1,5,0) to (1,4,0)
.
Last edited by LongtimeAirman on Wed Jul 18, 2018 7:13 pm; edited 1 time in total (Reason for editing : Added P.S)
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
Pictures are essential for me too, I just create them in my mind though. I don't have any easy-to-use tools to make them into images. The tools I do have are not vector based, so they are a little bit clumsy to use.
Are all of my ideas difficult? Probably. The ones worth mentioning are. If I thought they were simple, I'd probably just assume that they are obvious to everyone and not go into detail about it. Which is a really bad assumption because others don't always see what I see and vice-versa.
Image Request: Create an image of the receiver particle, take one cardinal point and draw the axes that are used for the linear and tangential component at that point. The axes would be rendered like the axis marker in the above images (the arrows with X, Y and Z labels) but also extended into the negative regions of those dimensions, at least for the tangential components, the linear is not so important unless the negative is considered the repulsion direction for that cardinal point (such as East in my example).
Then create a second image, starting with the above image, and add in an emitter particle and a line from the center of that emitter to the cardinal point, just like you have above.
Then create a third image, starting with the first image above, not the second, add in the emitter from the second image and instead of drawing the line from the center to the cardinal point, draw the charge vector for that line with its base at the cardinal point.
What this shows is how the linear and tangential components are part of the charge vector. You will be able to see how to split that vector along those dimensions because it will show the angles between the charge vector and those axes. You will be able to see how the charge vector points more along one dimension than another, if applicable based on their relative positions.
I think we should diagram all of this algorithm, well, as much as possible, and I might write a paper about it: How to Approximate the Charge Field of a Charged Particle. We can flesh out everything here, which we have done a lot of already, and see if it is worth it or not. Of course, we should really make sure that it works before we go too far down that path.
I have been thinking about the precision of this model and how to improve it. It isn't really the time to be doing that, since we have no idea of how this algorithm will perform, but I thought it worth mentioning that we are not limited to 6 cardinal points. Of course, they won't be cardinal if we have more (some might be, but not all) so we may have to find a new term for them. Charge Points? Whatever, it isn't important right now. I was thinking about using a dodecahedron.

Which is a spherical shape containing 20 vertices. It is easy to add even more vertices to make it even more spherical. However, with 20 vertices, we are already heading into slowness. That is 20 charge calculations per other particle per particle. This would also mean that I can't use my re-orientation trick. That only works for the cardinal points because they can be aligned with the axes. Well, I could re-orient for each Charge Point I guess. We also need to be able to determine the Charge Point that is on the opposite side from each other Charge Point. This is feasible with a dodecahedron, but not as easy as with the cardinal points.
That will become more feasible if I can find a more efficient way to implement this in a shader. I am thinking about splitting it into 2 shaders if I can. Rather than calculating the 6 (or 20) Charge Points in series (a for loop), I want to be able to calculate them in parallel (which is what shaders do) and then combine them in the next shader. It will use more memory but should run a lot faster. If it is fast enough, then we can think about using more Charge Points for more precision.
But I'm probably just muddying the waters. Don't worry too much about improvements like that. There is plenty of time for that later, once we have a working prototype.
Are all of my ideas difficult? Probably. The ones worth mentioning are. If I thought they were simple, I'd probably just assume that they are obvious to everyone and not go into detail about it. Which is a really bad assumption because others don't always see what I see and vice-versa.
Image Request: Create an image of the receiver particle, take one cardinal point and draw the axes that are used for the linear and tangential component at that point. The axes would be rendered like the axis marker in the above images (the arrows with X, Y and Z labels) but also extended into the negative regions of those dimensions, at least for the tangential components, the linear is not so important unless the negative is considered the repulsion direction for that cardinal point (such as East in my example).
Then create a second image, starting with the above image, and add in an emitter particle and a line from the center of that emitter to the cardinal point, just like you have above.
Then create a third image, starting with the first image above, not the second, add in the emitter from the second image and instead of drawing the line from the center to the cardinal point, draw the charge vector for that line with its base at the cardinal point.
What this shows is how the linear and tangential components are part of the charge vector. You will be able to see how to split that vector along those dimensions because it will show the angles between the charge vector and those axes. You will be able to see how the charge vector points more along one dimension than another, if applicable based on their relative positions.
I think we should diagram all of this algorithm, well, as much as possible, and I might write a paper about it: How to Approximate the Charge Field of a Charged Particle. We can flesh out everything here, which we have done a lot of already, and see if it is worth it or not. Of course, we should really make sure that it works before we go too far down that path.
I have been thinking about the precision of this model and how to improve it. It isn't really the time to be doing that, since we have no idea of how this algorithm will perform, but I thought it worth mentioning that we are not limited to 6 cardinal points. Of course, they won't be cardinal if we have more (some might be, but not all) so we may have to find a new term for them. Charge Points? Whatever, it isn't important right now. I was thinking about using a dodecahedron.
Which is a spherical shape containing 20 vertices. It is easy to add even more vertices to make it even more spherical. However, with 20 vertices, we are already heading into slowness. That is 20 charge calculations per other particle per particle. This would also mean that I can't use my re-orientation trick. That only works for the cardinal points because they can be aligned with the axes. Well, I could re-orient for each Charge Point I guess. We also need to be able to determine the Charge Point that is on the opposite side from each other Charge Point. This is feasible with a dodecahedron, but not as easy as with the cardinal points.
That will become more feasible if I can find a more efficient way to implement this in a shader. I am thinking about splitting it into 2 shaders if I can. Rather than calculating the 6 (or 20) Charge Points in series (a for loop), I want to be able to calculate them in parallel (which is what shaders do) and then combine them in the next shader. It will use more memory but should run a lot faster. If it is fast enough, then we can think about using more Charge Points for more precision.
But I'm probably just muddying the waters. Don't worry too much about improvements like that. There is plenty of time for that later, once we have a working prototype.
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
.
The following example begins with emission direction lines but also includes projecting the charge density vectors received into their perpendicular and tangential axii at each of the cardinal positions.


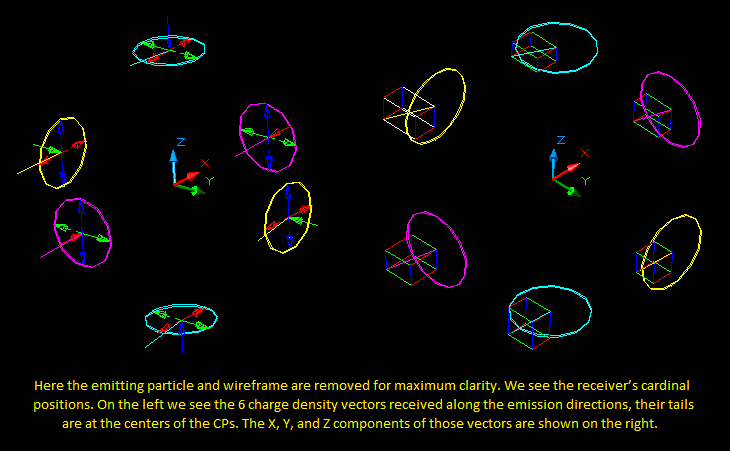

.
The following example begins with emission direction lines but also includes projecting the charge density vectors received into their perpendicular and tangential axii at each of the cardinal positions.




.
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
There's too much going on in those images. Focus on a single cardinal point and don't worry about text. You can put the text into your post to explain them, but there won't be any need to put it in the image. Don't be afraid to zoom in on the cardinal point when showing something that only requires the area around that point to be in view.
The boxes around the charge vectors just hide them. I can't tell if those charge vectors are pointing in the right direction or not.
I'm not sure what those discs are trying to show, but they just get in the way. I assume it is the possible spin component directions. They might be better if they were transparent but I don't think they are needed.
Maybe make the charge vectors use a thicker line to render than the dimension markers on the cardinal points. We want the charge vectors to stand out as they are the important part.
The boxes around the charge vectors just hide them. I can't tell if those charge vectors are pointing in the right direction or not.
I'm not sure what those discs are trying to show, but they just get in the way. I assume it is the possible spin component directions. They might be better if they were transparent but I don't think they are needed.
Maybe make the charge vectors use a thicker line to render than the dimension markers on the cardinal points. We want the charge vectors to stand out as they are the important part.
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
I have just pushed some commits to GIT that have a working algorithm!
Use the test.html file to see it in action. I have created 2 charged particles that sit above and below each other so they are pole to pole. I also changed the charge density array to contain negative coefficients in the polar region (simulating attraction) and got some very interesting results.
The 2 particles are attracted to each other because they are in the polar region of the other particle. They move towards each other until they get deep enough that the charge repulsion from the equatorial region pushes them apart again. They move apart until the repulsion is gone and the attraction brings them back together again. They just bob up and down. It's so simple but it just blows me away! It means the algorithms are working as intended!
Then I took one of the particles and oriented it to emit down into the pole of the other. It pushes the other particle away but the other particles pole attracts it back, so the re-oriented particle chases the other one!
I also did the standard test of 2 particles, equator to equator, and they boringly moved apart.
You can play with it by setting the initial state of the particles. You can even add more if you want. I haven't tested that yet but the principle is the same. Go to line 119 of test.html to the initParticles function. You can see how to set the positions and there is a commented out line that shows how to set the orientation.
Have fun!
Use the test.html file to see it in action. I have created 2 charged particles that sit above and below each other so they are pole to pole. I also changed the charge density array to contain negative coefficients in the polar region (simulating attraction) and got some very interesting results.
The 2 particles are attracted to each other because they are in the polar region of the other particle. They move towards each other until they get deep enough that the charge repulsion from the equatorial region pushes them apart again. They move apart until the repulsion is gone and the attraction brings them back together again. They just bob up and down. It's so simple but it just blows me away! It means the algorithms are working as intended!
Then I took one of the particles and oriented it to emit down into the pole of the other. It pushes the other particle away but the other particles pole attracts it back, so the re-oriented particle chases the other one!
I also did the standard test of 2 particles, equator to equator, and they boringly moved apart.
You can play with it by setting the initial state of the particles. You can even add more if you want. I haven't tested that yet but the principle is the same. Go to line 119 of test.html to the initParticles function. You can see how to set the positions and there is a commented out line that shows how to set the orientation.
Have fun!
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
I just added a third particle (and fixed some bugs) and put them all one above the other. The middle particle gets bounced between the other 2, who are also bouncing up and down. Its a cool little dance that isn't exactly smooth as the middle particle is feeling forces from the other 2.
I then offset the middle particle in the X dimension and was amazed again as all particles pulled each other inwards (the middle particle sliding perfectly along the X axis) and then repulsed each other, causing them all to spin away.
I really wasn't expecting it to work this good without some serious tweaks. I felt the theory was sound, but not so sure that I had it all figured out in the math. I can't stop smiling! I'm really, really impressed with it. That doesn't mean it is perfect. I'm sure there are still problems and improvements to be made. The whole charge density algorithm can be replaced for one thing, but even with this fairly crude approximation it is working beautifully.
I'm sorry I can't show everyone else. You probably think I've finally gone mad, going crazy over some bouncing balls.
I then offset the middle particle in the X dimension and was amazed again as all particles pulled each other inwards (the middle particle sliding perfectly along the X axis) and then repulsed each other, causing them all to spin away.
I really wasn't expecting it to work this good without some serious tweaks. I felt the theory was sound, but not so sure that I had it all figured out in the math. I can't stop smiling! I'm really, really impressed with it. That doesn't mean it is perfect. I'm sure there are still problems and improvements to be made. The whole charge density algorithm can be replaced for one thing, but even with this fairly crude approximation it is working beautifully.
I'm sorry I can't show everyone else. You probably think I've finally gone mad, going crazy over some bouncing balls.
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
After my excitement died down a bit, I set about cleaning up the initialization code so that it was easier to choose between various models for testing. The initParticles function now has a list of other functions (which all have a function name like init*Body*, eg initThreeBody02) that will create a ParticleArray object with various particle configurations. You choose which one you want, uncomment it, comment out any of the others and then refresh the page. I need to setup a mechanism to do that in the app, rather than in the code. At that point I could upload a copy to my site for everyone else to play with.
Page 1 of 15 • 1, 2, 3 ... 8 ... 15 
 Similar topics
Similar topics» Modeling a Charge Particle
» Spinning Particle Language
» Particle Drifts in Space
» The First Ever Photograph of Light as both a Particle and Wave
» Physicists Finally Narrowed Down the Mass of the Tiniest 'Ghost Particle' in the Universe
» Spinning Particle Language
» Particle Drifts in Space
» The First Ever Photograph of Light as both a Particle and Wave
» Physicists Finally Narrowed Down the Mass of the Tiniest 'Ghost Particle' in the Universe
Page 1 of 15
Permissions in this forum:
You cannot reply to topics in this forum