Animate the PI = 4 experiment
+2
Vexman
Cr6
6 posters
Page 1 of 8
Page 1 of 8 • 1, 2, 3, 4, 5, 6, 7, 8 
 Animate the PI = 4 experiment
Animate the PI = 4 experiment
.
Hey Nevyn, I was working on the Virtual Scattering Application, reviewing the spheres’ motion on the Revolving gun tracks when it occurred to me; you could -
Animate the PI = 4 experiment!
The animation might allow the user to slow down the action and take a closer look at the separate motions, identify the curving ball’s orthogonal velocity vectors and compare the two paths.
Of course StevenO’s experimental results will be one documented source that the animation would cite. Miles might even see fit to comment.
I couldn’t wait to share this idea. I haven’t stopped to think about it for a moment, it’s only been in the back of my mind for a few years. It’s easy enough. If you let me help that’d be great; although I believe my slovenly lackadaisical programming habits have stressed your patience to a limit, such that you might appreciate an early break from the Virtual Scattering Application project.
.
Hey Nevyn, I was working on the Virtual Scattering Application, reviewing the spheres’ motion on the Revolving gun tracks when it occurred to me; you could -
Animate the PI = 4 experiment!
The animation might allow the user to slow down the action and take a closer look at the separate motions, identify the curving ball’s orthogonal velocity vectors and compare the two paths.
Of course StevenO’s experimental results will be one documented source that the animation would cite. Miles might even see fit to comment.
I couldn’t wait to share this idea. I haven’t stopped to think about it for a moment, it’s only been in the back of my mind for a few years. It’s easy enough. If you let me help that’d be great; although I believe my slovenly lackadaisical programming habits have stressed your patience to a limit, such that you might appreciate an early break from the Virtual Scattering Application project.
.
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
 Re: Animate the PI = 4 experiment
Re: Animate the PI = 4 experiment
Sorry, Airman, I must have missed this when you posted it.
This might be a good opportunity for you to take the next step and try to analyze the problem yourself. Producing a thorough description of the app and what it will contain. I don't always write this part down, but it is all in my head unless it gets very complicated. However, it really does pay to write it down and have something to refer to. Draw some diagrams, identify the important parts of the system, and find the relationships between them.
One good way to do this is to read the relevant papers and jot down the things that you think are important. Copy/paste paragraphs into a file for reference. Anything you think might be important, even if it doesn't end up being so. Watch the video and describe the setup, the motions, the expectations.
Once you have that, it is a little bit easier to start to model it with programming constructs.
This might be a good opportunity for you to take the next step and try to analyze the problem yourself. Producing a thorough description of the app and what it will contain. I don't always write this part down, but it is all in my head unless it gets very complicated. However, it really does pay to write it down and have something to refer to. Draw some diagrams, identify the important parts of the system, and find the relationships between them.
One good way to do this is to read the relevant papers and jot down the things that you think are important. Copy/paste paragraphs into a file for reference. Anything you think might be important, even if it doesn't end up being so. Watch the video and describe the setup, the motions, the expectations.
Once you have that, it is a little bit easier to start to model it with programming constructs.
 Re: Animate the PI = 4 experiment
Re: Animate the PI = 4 experiment
.
I take it that means you like the idea? If so, please accept my strongest recommendation - change the track type.
I think a PI = 4 animation should link/refer to Miles', A Simple Experiment Proves π = 4
http://milesmathis.com/pi7.pdf , or https://www.nevyns-lab.com/mathis/mirror/milesmathis.com/pi7.pdf
A brief review. Miles has had plenty of practice, and does what I believe is his best job yet, clarifying the PI=4 mainstream misunderstanding, based on history and a geometry that never included a time variable. Sure, PI equals 3.14 for geometry, but when circular motion – including time - is involved, PI = 4.
https://youtu.be/QhuvUSS3KAE
Miles begins the paper by announcing Steven Oostdijk’s success in conducting the PI = 4 experiment, providing the youtube video link included here;
Miles mentions that the experiment was actually first conducted by Jeff Cosman using his children's' wooden toy tracks - deemed too easy to dismiss. StevenO volunteered to do the experiment with clear pvc tubing.
For a PI=4 animation I would strongly suggest we recreate the experiment using an alternative concave track, or dual rails, anything other than clear plastic tubing. I gave up my own personal effort to recreate the PI=4 experiment primarily due to my problems working with PVC tubing. First, it would change length based on temperature time of day. Looking straight down the tubes ends the paths never remained at a constant height, it had dips and heights determined by where the tracks were taped down. Worse, when tubing is used, the circular track cannot smoothly merge with straight tube leading to the circular path since they both cannot occupy the same space at the same time.
With all due respect – understanding the material limitations that StevenO faced, please note that the tubing he used for his shorter track, - show at left in the image below - curve up and over the metal ends of the pvc table, as indicated by the tube’s shadow. I can see the taped down sections have deformed the tube's top surface. Note that the ‘circular track is more oblong or pear shaped and pinched at start/end of the circular tracks end - there's no way for the tubes to come together closely without deforming each other. That may not be an a problem with an animation but intersecting tubes may be too complex. Rails, on the other hand, rather than toy tracks, have switches that join straight and curved sections. A concave track doesn’t have that problem, the two paths can simply merge or diverge like properly intersecting tubes.

I've got plenty for starters, including 3D autocad drawings of StevenO’s smaller track, as well as my PI=4 design. My gantry and release mechanism still brings a lump to my throat. I posted about it here somewhere - almost three years ago. Shortly after beginning I needed some additional length and was happy to find it would fit on my table’s diagonal. Works for me. Even better, after Miles' subsequent Track paper I re-created all of the lines for a standard 400 meter track in R and autocad.
Do you have an industry form used to organize one's thoughts?
.
I take it that means you like the idea? If so, please accept my strongest recommendation - change the track type.
I think a PI = 4 animation should link/refer to Miles', A Simple Experiment Proves π = 4
http://milesmathis.com/pi7.pdf , or https://www.nevyns-lab.com/mathis/mirror/milesmathis.com/pi7.pdf
A brief review. Miles has had plenty of practice, and does what I believe is his best job yet, clarifying the PI=4 mainstream misunderstanding, based on history and a geometry that never included a time variable. Sure, PI equals 3.14 for geometry, but when circular motion – including time - is involved, PI = 4.
https://youtu.be/QhuvUSS3KAE
Miles begins the paper by announcing Steven Oostdijk’s success in conducting the PI = 4 experiment, providing the youtube video link included here;
8:57 in length. 13,619 views. No comments. SUBSCRIBE 100.Extraordinary Experiments
Published on Sep 21, 2016
PI is not what you are used to for things in motion.
Experiment that shows that, while Pi as a distance is 3.14, Pi as a distance/time is 4.
Based on the paper "The extinction of Pi" by Miles Mathis.
Miles mentions that the experiment was actually first conducted by Jeff Cosman using his children's' wooden toy tracks - deemed too easy to dismiss. StevenO volunteered to do the experiment with clear pvc tubing.
For a PI=4 animation I would strongly suggest we recreate the experiment using an alternative concave track, or dual rails, anything other than clear plastic tubing. I gave up my own personal effort to recreate the PI=4 experiment primarily due to my problems working with PVC tubing. First, it would change length based on temperature time of day. Looking straight down the tubes ends the paths never remained at a constant height, it had dips and heights determined by where the tracks were taped down. Worse, when tubing is used, the circular track cannot smoothly merge with straight tube leading to the circular path since they both cannot occupy the same space at the same time.
With all due respect – understanding the material limitations that StevenO faced, please note that the tubing he used for his shorter track, - show at left in the image below - curve up and over the metal ends of the pvc table, as indicated by the tube’s shadow. I can see the taped down sections have deformed the tube's top surface. Note that the ‘circular track is more oblong or pear shaped and pinched at start/end of the circular tracks end - there's no way for the tubes to come together closely without deforming each other. That may not be an a problem with an animation but intersecting tubes may be too complex. Rails, on the other hand, rather than toy tracks, have switches that join straight and curved sections. A concave track doesn’t have that problem, the two paths can simply merge or diverge like properly intersecting tubes.

I've got plenty for starters, including 3D autocad drawings of StevenO’s smaller track, as well as my PI=4 design. My gantry and release mechanism still brings a lump to my throat. I posted about it here somewhere - almost three years ago. Shortly after beginning I needed some additional length and was happy to find it would fit on my table’s diagonal. Works for me. Even better, after Miles' subsequent Track paper I re-created all of the lines for a standard 400 meter track in R and autocad.
Do you have an industry form used to organize one's thoughts?
.
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
 Re: Animate the PI = 4 experiment
Re: Animate the PI = 4 experiment
.
https://www.youtube.com/watch?time_continue=66&v=2-iqu1EOcyo
Minimalist Marble Machine
This youtube link is an example of a two-rail track I had to share.
.
https://www.youtube.com/watch?time_continue=66&v=2-iqu1EOcyo
Minimalist Marble Machine
35,310 views
Tinkerlog
Published on Feb 24, 2015
Made out of brass and african padouk.
More at http://tinkerlog.com/2015/02/24/minim...
This youtube link is an example of a two-rail track I had to share.
.
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
 Re: Animate the PI = 4 experiment
Re: Animate the PI = 4 experiment
.
I considered other changes, but decided against it after having reread most of the thread, Proof that pi=4 https://milesmathis.forumotion.com/t226-proof-that-pi4#1531 including StevenO's ( Steven Oostdijk - soostdijk ) comments we posted here almost three years ago.
Re-reading was a humbling reminder - I certainly need to understand circular motion better! But don't we all? I’m grateful StevenO shared his observations. He also revealed he had checked and found the ball exiting the circular track travels at velocity ratio (PI/4) compared to the straight track (4). He didn’t make those results public since he could not properly explain the changes in momentum. Let people absorb the fact that PI = 4 first.
So, unless there are any objections, along with the track type change I requested, I propose we stick to the same PI = 4 configuration that StevenO used. Say A rendering of flat tabletop model containing two side-by-side tracks, one circular of length 3.14, and the other straight with length of 4. Balls are released at the start of each track simultaneously and can be observed to cross each tracks’ -1 through 4 also simultaneously. Given a continuous loop of marbles, an Orbital camera – as opposed to fixed model views over each mark – should suffice.
.
I considered other changes, but decided against it after having reread most of the thread, Proof that pi=4 https://milesmathis.forumotion.com/t226-proof-that-pi4#1531 including StevenO's ( Steven Oostdijk - soostdijk ) comments we posted here almost three years ago.
Re-reading was a humbling reminder - I certainly need to understand circular motion better! But don't we all? I’m grateful StevenO shared his observations. He also revealed he had checked and found the ball exiting the circular track travels at velocity ratio (PI/4) compared to the straight track (4). He didn’t make those results public since he could not properly explain the changes in momentum. Let people absorb the fact that PI = 4 first.
So, unless there are any objections, along with the track type change I requested, I propose we stick to the same PI = 4 configuration that StevenO used. Say A rendering of flat tabletop model containing two side-by-side tracks, one circular of length 3.14, and the other straight with length of 4. Balls are released at the start of each track simultaneously and can be observed to cross each tracks’ -1 through 4 also simultaneously. Given a continuous loop of marbles, an Orbital camera – as opposed to fixed model views over each mark – should suffice.
.
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
 Re: Animate the PI = 4 experiment
Re: Animate the PI = 4 experiment
.
After his brief introduction to his youtube video, PI is not what you are used to for things in motion. StevenO directs the viewer to Miles’
351. The Extinction of π. http://milesmathis.com/pi2.html Here I show that the true value of π, defined as the ratio of circumference to diameter, is 4. 15pp.
Or available at Nevyn's mirror.
https://www.nevyns-lab.com/mathis/mirror/milesmathis.com/pi2.html
Beyond that, StevenO uses as little math as possible, that seems like the wise thing to do. Here are two examples: Diagrams and descriptions intended to convey the difference between linear and curved motion. Here are the two sets of descriptions.

So I took his advice and re-read The Extinction of PI. That’s always a good thing. Trying to apply to the topic at hand, if it were up to me to describe circular motion, besides immediately redirecting that person to Miles work, I might attempt to draw and describe Miles’s AC = AB-BD+DC vector diagram. Or discuss the so called Hilbert or Manhattan metric. Cycloid math is fine.
With so many interpretations we might provide pertinent diagrams and descriptions on on/off-able internal scene walls?
.
Oh, the math.Airman wrote. “The animation might allow the user to slow down the action and take a closer look at the separate motions, identify the curving ball’s orthogonal velocity vectors and compare the two paths”.
After his brief introduction to his youtube video, PI is not what you are used to for things in motion. StevenO directs the viewer to Miles’
351. The Extinction of π. http://milesmathis.com/pi2.html Here I show that the true value of π, defined as the ratio of circumference to diameter, is 4. 15pp.
Or available at Nevyn's mirror.
https://www.nevyns-lab.com/mathis/mirror/milesmathis.com/pi2.html
Beyond that, StevenO uses as little math as possible, that seems like the wise thing to do. Here are two examples: Diagrams and descriptions intended to convey the difference between linear and curved motion. Here are the two sets of descriptions.
Ok, I think I'm done picking on StevenO. I hope to do at least half as well. Math is a big can of worms. Maybe including vectors tied to the moving spheres as a possible alternative isn’t being very realistic.1. Geometric Pi: integrating two variables, x and y.
Kinematic Pi: integrating three variables, x, y and t (time). Accelerations required for motion in a curve. Velocity moves only in a straight line.
2. The ratio of distance and time on the straight path is a linear function.
The ratio of distance and time on the circular path is a cycloid function. The total length of the cycloid is 4 diameter.

So I took his advice and re-read The Extinction of PI. That’s always a good thing. Trying to apply to the topic at hand, if it were up to me to describe circular motion, besides immediately redirecting that person to Miles work, I might attempt to draw and describe Miles’s AC = AB-BD+DC vector diagram. Or discuss the so called Hilbert or Manhattan metric. Cycloid math is fine.
With so many interpretations we might provide pertinent diagrams and descriptions on on/off-able internal scene walls?
.
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
 Re: Animate the PI = 4 experiment
Re: Animate the PI = 4 experiment
No, I don't know of any templates or forms for building an app outline. Just put it all together in some file, I just use a text file, but you could use Word, Google Docs, anything. The important thing is to find what you need to model. Focusing on the physical setup will provide most of that. Then you just need to work out how to apply the math. The math is the guts of this kind of app. It should be the center piece, even before the 3D scene. You don't even need a scene. Just work it as a number cruncher first and then apply some 3D objects to it. If you focus on the 3D part too much, you may end up tying yourself in knots.
A common way to develop apps is the Model-View-Controller paradigm (MVC). You split the problem down into those 3 things. The Model contains the data and is what gets operated on. The View just provides a visual representation of the Model. The Controller manipulates the Model. This provides a clean separation so you can focus on each one individually. The View knows nothing about the Controller, only the Model. The Controller knows nothing about the View, again, only the Model. The Model knows nothing about anything (it's the Jon Snow of MVC's). Okay, that is a little harsh, it does know about the data and that is the most important part of it all.
You can have many different Views and many different Controllers, but you will only have one Model. Some apps may actually have multiple Models, but each one would have their own Views and Controllers, so can be seen as a separate thing. You won't need multiple Models in this app.
So in this case, the Model may just be a couple of balls and a couple of tracks. I'm not sure how to represent the tracks as it feels like they are just math and not really an entity. It probably comes down to how the balls achieve motion. In reality, we use gravity to provide force and the track to provide a path, but in an app we can just give it a velocity, so we don't need gravity. We do still need some idea of where the balls move. The curved sections effectively add a new velocity at each point of the curve.
So we could represent the track by a series of vectors, each a velocity, that get added to the ball as it passes that point. The first part of the track gives the ball its initial velocity and any other straight sections are zero's. The curved sections contain vectors that give it a kick sideways. They do get tricky though. We can't just associate a track velocity with a position as we don't know if the ball will actually end up on that position at runtime. It could end up part way between positions. So we really need to treat it more mathematically. We need to focus on the fact that we are trying to demonstrate PI, not just running a ball around a track.
So the curved sections of track need to take the exact position of the ball into account and determine the velocity to add, using PI. This may mean that we can just give each track section a type (straight or curved) and let the Controller take care of calculating the velocities at runtime.
What I'm trying to get at is that you can break things down into more manageable pieces. I didn't mean to actually get into implementation details, but I thought an example would probably convey more information than a heap of words. In essence, we need to find a way to express the math in the existing constructs. In this case, the frame based execution is the existing construct and the path of the balls is what we need to fit into it. We need to find a way to calculate the next vector to apply to the ball, given its current position and velocity. The way the track is represented is crucial to that.
I am thinking that the track is a series of segments and each one has a type, starting position and a length (may be a vector to provide direction as well as length). The type just tells us if it is straight or curved. We assume a complete circle for the curved section. Now we have to determine how we use the length of a curved section to calculate the path. This is a little bit more tricky than it looks.
The problem is which PI do we use? If we only have a length, which is really the circumference, then how do we use that to determine the circle? It seems to me that we should use 3.14, what I call PIg for geometric as opposed to PIk for kinematic. Once we use that to get the radius of the circle, we use PIk to calculate the velocity to add to the ball. However, I'm not 100% sure of that and am open to arguments for and against. Of course, we could just skip it and define the curved sections with a radius instead of a length. Although, even doing that, we still need to figure out how long the corresponding straight section must be to match it, so it seems we can't avoid it.
I wonder if SteveO thought about that and calculated his marks appropriately?
A common way to develop apps is the Model-View-Controller paradigm (MVC). You split the problem down into those 3 things. The Model contains the data and is what gets operated on. The View just provides a visual representation of the Model. The Controller manipulates the Model. This provides a clean separation so you can focus on each one individually. The View knows nothing about the Controller, only the Model. The Controller knows nothing about the View, again, only the Model. The Model knows nothing about anything (it's the Jon Snow of MVC's). Okay, that is a little harsh, it does know about the data and that is the most important part of it all.
You can have many different Views and many different Controllers, but you will only have one Model. Some apps may actually have multiple Models, but each one would have their own Views and Controllers, so can be seen as a separate thing. You won't need multiple Models in this app.
So in this case, the Model may just be a couple of balls and a couple of tracks. I'm not sure how to represent the tracks as it feels like they are just math and not really an entity. It probably comes down to how the balls achieve motion. In reality, we use gravity to provide force and the track to provide a path, but in an app we can just give it a velocity, so we don't need gravity. We do still need some idea of where the balls move. The curved sections effectively add a new velocity at each point of the curve.
So we could represent the track by a series of vectors, each a velocity, that get added to the ball as it passes that point. The first part of the track gives the ball its initial velocity and any other straight sections are zero's. The curved sections contain vectors that give it a kick sideways. They do get tricky though. We can't just associate a track velocity with a position as we don't know if the ball will actually end up on that position at runtime. It could end up part way between positions. So we really need to treat it more mathematically. We need to focus on the fact that we are trying to demonstrate PI, not just running a ball around a track.
So the curved sections of track need to take the exact position of the ball into account and determine the velocity to add, using PI. This may mean that we can just give each track section a type (straight or curved) and let the Controller take care of calculating the velocities at runtime.
What I'm trying to get at is that you can break things down into more manageable pieces. I didn't mean to actually get into implementation details, but I thought an example would probably convey more information than a heap of words. In essence, we need to find a way to express the math in the existing constructs. In this case, the frame based execution is the existing construct and the path of the balls is what we need to fit into it. We need to find a way to calculate the next vector to apply to the ball, given its current position and velocity. The way the track is represented is crucial to that.
I am thinking that the track is a series of segments and each one has a type, starting position and a length (may be a vector to provide direction as well as length). The type just tells us if it is straight or curved. We assume a complete circle for the curved section. Now we have to determine how we use the length of a curved section to calculate the path. This is a little bit more tricky than it looks.
The problem is which PI do we use? If we only have a length, which is really the circumference, then how do we use that to determine the circle? It seems to me that we should use 3.14, what I call PIg for geometric as opposed to PIk for kinematic. Once we use that to get the radius of the circle, we use PIk to calculate the velocity to add to the ball. However, I'm not 100% sure of that and am open to arguments for and against. Of course, we could just skip it and define the curved sections with a radius instead of a length. Although, even doing that, we still need to figure out how long the corresponding straight section must be to match it, so it seems we can't avoid it.
I wonder if SteveO thought about that and calculated his marks appropriately?
 Re: Animate the PI = 4 experiment
Re: Animate the PI = 4 experiment
Thanks Nevyn, the Model-View-Controller paradigm (MVC) sounds fine.
I’m fairly certain StevenO based his dimensions on the circle’s diameter. The first measurement shown is the circle with 16 cm diameter. We then see the circumference measurement, 50.5 cm. 50.5/16 is 3.15 which is close to PI, but nowhere near 4… . How does he intend to show PI = 4?
I believe the main point being made is that when the experiment is run, we will see that PI = 4. That is the same as saying that it takes 4X as long to travel along the circle’s curved path as it takes to travel the circle’s straight diameter. 16 cm is the inside diameter to the circular track. Adding the pvc hose about that circle results in a circular track centerline diameter of 17.6 cm. Note that the length between each of the straight path marks (0-4) is equal to a diameter, 4 x 17.6. or 70.4cm.
This is an initial effort to identify the main points or considerations that occurred to me. Feel free to redline as you like.

A. Let S be is the starting point for both tracks. Balls in the S position will remain there until they are somehow set in motion. A mechanism is required - such as a gate - that will release both balls at the same time.
B. The Section labelled B is the acceleration ramp, the track section between S and -1. Since we are animating the PI = 4 experiment - which was conducted under gravity – let’s stick with the gravity assist ramp. We might vary the ball velocities by adjusting the ramp angle. That wouldn’t change the PI = 4 outcome – again, within the physical limits of rolling friction etc. The bottom ends of the ramp should be curved to allow a smooth transition to the following straight sections (-1 to 0).
C. At the -1 marker, the ramp ends. Both balls have been given their track velocities.
D. Section D is intended as a means to determine the time it takes to travel the straight diameter.
E. Marker point zero.
F. The start of the “curved track’s curve.
G. The start of the straight track.
H. The end of the “curved track’s curve.
I. The end of the “curved track’s curve.
It will be observed that the balls on either track will pass Markers 1 2 and 3 almost simultaneously. It should be surprising that when the Pig length is reached the ball in the curved path is not at its end, but is at a little past 3.
J. The end of the straight track. We can see that both balls have reached their ends at the same time.
K. There needs to me a mechanism to remove the balls from the track and reposition them back at the start.
Sorry I don’t quite follow your idea of having sections ‘add’ their velocities to the balls. Sounds like a conveyor system. The vector diagram I included yesterday, and the quote above refers is what Miles suggests is the only sort of valid means of comparing velocities and accelerations. Of course I’d probably use it incorrectly. ArcAC = AD + DC. Can we use those vectors as your segment velocities?
.
Nevyn wrote. The problem is which PI do we use? If we only have a length, which is really the circumference, then how do we use that to determine the circle? It seems to me that we should use 3.14, what I call PIg for geometric as opposed to PIk for kinematic.
I’m fairly certain StevenO based his dimensions on the circle’s diameter. The first measurement shown is the circle with 16 cm diameter. We then see the circumference measurement, 50.5 cm. 50.5/16 is 3.15 which is close to PI, but nowhere near 4… . How does he intend to show PI = 4?
I believe the main point being made is that when the experiment is run, we will see that PI = 4. That is the same as saying that it takes 4X as long to travel along the circle’s curved path as it takes to travel the circle’s straight diameter. 16 cm is the inside diameter to the circular track. Adding the pvc hose about that circle results in a circular track centerline diameter of 17.6 cm. Note that the length between each of the straight path marks (0-4) is equal to a diameter, 4 x 17.6. or 70.4cm.
This is an initial effort to identify the main points or considerations that occurred to me. Feel free to redline as you like.

A. Let S be is the starting point for both tracks. Balls in the S position will remain there until they are somehow set in motion. A mechanism is required - such as a gate - that will release both balls at the same time.
B. The Section labelled B is the acceleration ramp, the track section between S and -1. Since we are animating the PI = 4 experiment - which was conducted under gravity – let’s stick with the gravity assist ramp. We might vary the ball velocities by adjusting the ramp angle. That wouldn’t change the PI = 4 outcome – again, within the physical limits of rolling friction etc. The bottom ends of the ramp should be curved to allow a smooth transition to the following straight sections (-1 to 0).
C. At the -1 marker, the ramp ends. Both balls have been given their track velocities.
D. Section D is intended as a means to determine the time it takes to travel the straight diameter.
E. Marker point zero.
F. The start of the “curved track’s curve.
G. The start of the straight track.
H. The end of the “curved track’s curve.
I. The end of the “curved track’s curve.
It will be observed that the balls on either track will pass Markers 1 2 and 3 almost simultaneously. It should be surprising that when the Pig length is reached the ball in the curved path is not at its end, but is at a little past 3.
J. The end of the straight track. We can see that both balls have reached their ends at the same time.
K. There needs to me a mechanism to remove the balls from the track and reposition them back at the start.
Quoting from, The Extinction of PI. After we have made all these corrections, we are in a position to see that we may assign the acceleration a to the line segment BC. Furthermore, if a = v2/2r, and AB = r, then r = v, and a = r/2. Consulting the diagram above again, that is also 2BC = CO. What this means is that we have a new way to find a centripetal acceleration, currently called gravity. The equation a = r/2 gives us a total acceleration over 1/8th of the orbit, so the total acceleration over the entire orbit is 4r.
Sorry I don’t quite follow your idea of having sections ‘add’ their velocities to the balls. Sounds like a conveyor system. The vector diagram I included yesterday, and the quote above refers is what Miles suggests is the only sort of valid means of comparing velocities and accelerations. Of course I’d probably use it incorrectly. ArcAC = AD + DC. Can we use those vectors as your segment velocities?
.
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
 Re: Animate the PI = 4 experiment
Re: Animate the PI = 4 experiment
Certain sections add velocity, but not all. Only the initial straight segment, which replicates the gravity component of the real experiment, and the curved section add velocity. A curve always adds velocity, hence why it is called an acceleration. It is the addition of 2 velocities. The velocity added by the curved section represents the resistance of the path, imparted onto the ball, causing it to change from its forward direction. Basically, the curve velocity represents the collision with the wall.
Here's my thoughts so far.
When the animation starts, the balls are given an initial push. This is a once off thing. Probably don't need to associate that with the first section of track, it will just be a part of the process, or may even be a property of the balls so that they just start with that velocity. While implementing gravity might be more realistic, it is unnecessary. The only reason for using gravity in reality is that it gives both balls an equal push. We can do that without gravity and it will be so much simpler.
On each frame, the current position of each ball is checked and the appropriate section of track found. If it is a straight section, then continue on without change. If it is a curved section, then add the calculated velocity caused by the curve, using PI=4, to that ball. If it is an end section, then stop the animation, reset to start, whatever it is we want it to do.
The tricky part is when the ball is currently in a straight section but will transition into a curved section during this frame. We will need to handle that in 2 parts so that the curve is applied at the right time. Not a difficult thing to do, it just needs to be remembered and applied. Essentially, we not only need to find the section of track that the ball is currently in, but also the section(s) that it will move into with its current velocity (not the velocity we are about to calculate for that frame).
If you remember back to the Particle Interaction Model app, we had to change the way it calculated each frame such that it ignored real-time and just made changes assuming that 1/60th of a second had passed. We will need to do that again here.
Here's my thoughts so far.
When the animation starts, the balls are given an initial push. This is a once off thing. Probably don't need to associate that with the first section of track, it will just be a part of the process, or may even be a property of the balls so that they just start with that velocity. While implementing gravity might be more realistic, it is unnecessary. The only reason for using gravity in reality is that it gives both balls an equal push. We can do that without gravity and it will be so much simpler.
On each frame, the current position of each ball is checked and the appropriate section of track found. If it is a straight section, then continue on without change. If it is a curved section, then add the calculated velocity caused by the curve, using PI=4, to that ball. If it is an end section, then stop the animation, reset to start, whatever it is we want it to do.
The tricky part is when the ball is currently in a straight section but will transition into a curved section during this frame. We will need to handle that in 2 parts so that the curve is applied at the right time. Not a difficult thing to do, it just needs to be remembered and applied. Essentially, we not only need to find the section of track that the ball is currently in, but also the section(s) that it will move into with its current velocity (not the velocity we are about to calculate for that frame).
If you remember back to the Particle Interaction Model app, we had to change the way it calculated each frame such that it ignored real-time and just made changes assuming that 1/60th of a second had passed. We will need to do that again here.
 Re: Animate the PI = 4 experiment
Re: Animate the PI = 4 experiment
Airman wrote:I’m fairly certain StevenO based his dimensions on the circle’s diameter. The first measurement shown is the circle with 16 cm diameter. We then see the circumference measurement, 50.5 cm. 50.5/16 is 3.15 which is close to PI, but nowhere near 4… . How does he intend to show PI = 4?
The experiment would only show PIk=4 if the circle is calculated using PI=3.14. Setting up the circle is a geometric problem. The ball moving along the circuit is a kinematic problem.
 Re: Animate the PI = 4 experiment
Re: Animate the PI = 4 experiment
.
That reminds me. Rolling. I believe we both want to see the balls rolling – correct?. How difficult would that be? How does the ball roll in the curved track? Does the ball alternately rotate straight and to the side? I don’t think so.
I like your plan for locating each ball then applying the appropriate straight or curved formula. Taking care to check ahead for changes between straight and curved tracks sounds a lot like anticipating collisions.
Since you mentioned it, I’ve tried to see the tracks as necessary entities or not. I’d say they give the viewer something to focus on and consider. A track helps the viewer find and monitor the balls positions. Without tracks two balls flying through space – one straight and one curved - seems like something Microsoft displays during a pause in data exchanges; hourglasses represent ridiculously long periods of time for a computer user. I’d argue to keep the tracks.
Alrighty, we can do without an acceleration ramp. As such, would you agree that this app is now an almost flat – just a track and ball’s height - app. It may be more appropriately rendered in 2D.

The updated model diagram.
A. The negOne marker. Two balls with equal velocities will enter their tracks at the negOne markers simultaneously.
B. For both tracks, the initial straight section B (-1 to 0) is the length of the circle tracks diameter. What is important is that the viewer can see both balls entering their NegOne markers together, then both can be seen reaching their zero markers together, visual proof that the balls in either track have the same initial velocity.
C. Marker point zero.
D. The end of the curved track’s curve. There may need to be a track switch.
E. The start of the curved track’s curve. There may need to be a second track switch.
F. The start of the straight track.
G. Lengths between the straight track markers are equal to one circular track diameter. It will be observed that the balls on either track will pass their 1 2 and 3 markers almost simultaneously. It should be surprising that when the the PIg length is reached in the straight track, the ball in the curved path is not at its end, but is at a bit past 3.
H. The end of the straight track. We can see that both balls have reached their ends at the same time.
I. There needs to me a mechanism to remove the balls from the track and re-position them back at the start (?).
Miles’ arc, velocity and acceleration diagram seems important enough to me to include with the application. I've got to re-read The Extinction of PI paper a few more times.
Sorry, I didn't see your last post Nevyn, I'll get to it, I think I understand the problem. Must go now.
.
Basically, the curve velocity represents the collision with the wall
That reminds me. Rolling. I believe we both want to see the balls rolling – correct?. How difficult would that be? How does the ball roll in the curved track? Does the ball alternately rotate straight and to the side? I don’t think so.
I like your plan for locating each ball then applying the appropriate straight or curved formula. Taking care to check ahead for changes between straight and curved tracks sounds a lot like anticipating collisions.
Since you mentioned it, I’ve tried to see the tracks as necessary entities or not. I’d say they give the viewer something to focus on and consider. A track helps the viewer find and monitor the balls positions. Without tracks two balls flying through space – one straight and one curved - seems like something Microsoft displays during a pause in data exchanges; hourglasses represent ridiculously long periods of time for a computer user. I’d argue to keep the tracks.
Alrighty, we can do without an acceleration ramp. As such, would you agree that this app is now an almost flat – just a track and ball’s height - app. It may be more appropriately rendered in 2D.

The updated model diagram.
A. The negOne marker. Two balls with equal velocities will enter their tracks at the negOne markers simultaneously.
B. For both tracks, the initial straight section B (-1 to 0) is the length of the circle tracks diameter. What is important is that the viewer can see both balls entering their NegOne markers together, then both can be seen reaching their zero markers together, visual proof that the balls in either track have the same initial velocity.
C. Marker point zero.
D. The end of the curved track’s curve. There may need to be a track switch.
E. The start of the curved track’s curve. There may need to be a second track switch.
F. The start of the straight track.
G. Lengths between the straight track markers are equal to one circular track diameter. It will be observed that the balls on either track will pass their 1 2 and 3 markers almost simultaneously. It should be surprising that when the the PIg length is reached in the straight track, the ball in the curved path is not at its end, but is at a bit past 3.
H. The end of the straight track. We can see that both balls have reached their ends at the same time.
I. There needs to me a mechanism to remove the balls from the track and re-position them back at the start (?).
Miles’ arc, velocity and acceleration diagram seems important enough to me to include with the application. I've got to re-read The Extinction of PI paper a few more times.
Sorry, I didn't see your last post Nevyn, I'll get to it, I think I understand the problem. Must go now.
.
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
 Re: Animate the PI = 4 experiment
Re: Animate the PI = 4 experiment
We can show the track, I'm just trying to figure out how it needs to be represented in the code so that the processing is easier. However we represent it, it needs to contain enough information for the View to create a representation of it.
Here's a little task for you that we will need soon enough. Create some function(s) that calculate the lengths of the track segments and their markers. Given a radius for the circle, calculate all of the other parts. The track before the circle is not very important (with regards to its length) but I think we need enough length to show that the balls are moving at the same speed. Maybe half of the length of the track after the circle.
We could do all of this in 2D, but 3D allows the user to move around the apparatus. While the track is basically 2D, we don't need to be limited to that for the user.
Here's a little task for you that we will need soon enough. Create some function(s) that calculate the lengths of the track segments and their markers. Given a radius for the circle, calculate all of the other parts. The track before the circle is not very important (with regards to its length) but I think we need enough length to show that the balls are moving at the same speed. Maybe half of the length of the track after the circle.
We could do all of this in 2D, but 3D allows the user to move around the apparatus. While the track is basically 2D, we don't need to be limited to that for the user.
 Re: Animate the PI = 4 experiment
Re: Animate the PI = 4 experiment
.
Neither the circle nor straight path needs to be calculated. StevenO used his 16cm circle to create the 17.6 cm diameter circular track. He laid the straight track as 4 circular track diameters. StevenO was nice enough to unwind the circular track in order to mark its length against the adjacent four diameter straight length, marking it 3.14 - I daresay - without a calculator. Whether that’s true or not, he didn’t need to calculate using PIg.
Copy the task, generate the track segments and markers as a function of the circle's radius. Will do.
.
Airman. I must respectfully disagree. The experiment shows the motions of two balls, each traveling along either a straight or circular path – at equal velocities - reaching their 1 through 4 marks at the same time. The marks on the straight path coincides with the circular track’s diameter and circumference, demonstrating that PI(kinetic)= circumference/diameter = 4.Nevyn wrote. The experiment would only show PIk=4 if the circle is calculated using PI=3.14.
Neither the circle nor straight path needs to be calculated. StevenO used his 16cm circle to create the 17.6 cm diameter circular track. He laid the straight track as 4 circular track diameters. StevenO was nice enough to unwind the circular track in order to mark its length against the adjacent four diameter straight length, marking it 3.14 - I daresay - without a calculator. Whether that’s true or not, he didn’t need to calculate using PIg.
Airman. Agreed.Nevyn wrote. Setting up the circle is a geometric problem. The ball moving along the circuit is a kinematic problem.
Copy the task, generate the track segments and markers as a function of the circle's radius. Will do.
.
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
 Re: Animate the PI = 4 experiment
Re: Animate the PI = 4 experiment
.

Thanks for the tasking. The cyan image shown is the pvc track layout, which would need 5 parallel lines, the centerline plus inner and outer walls. The following function – I think it’s a function – should produce the same layout but with only three parallel lines, the centerline plus the track outline. I think it's what you requested, I don’t have a handy shell file to test it in and so haven't actually "run" it. Please point out errors.
P.S. Made a few corrections to the code, most important - the function now uses line material instead of mesh.
P.P.S. Haven't run the code but I cleaned up many typos. 14 Sept 0741
.

Thanks for the tasking. The cyan image shown is the pvc track layout, which would need 5 parallel lines, the centerline plus inner and outer walls. The following function – I think it’s a function – should produce the same layout but with only three parallel lines, the centerline plus the track outline. I think it's what you requested, I don’t have a handy shell file to test it in and so haven't actually "run" it. Please point out errors.
- Code:
//
// Draw PI = 4 Track Lines and Circles
//
function drawTracks( r ) {
var geometry = new THREE.BoxBufferGeometry( 200, 200, 200 );
var material = new THREE.LineBasicMaterial( { color: 'black' } );
// var r = 1;
var w = 0.1 * r; // track width
var q = 0.5 * r; // track separation
var cTrackCenter = new THREE.Vector3( 2*r*Math.PI, 2*r*Math.PI, 0 ) ;
// C track curved Outside edge
var geometry = new THREE.CircleBufferGeometry( r+w, 32 );
var circle = new THREE.Mesh( geometry, material );
circle.position.x = cTrackCenter.x;
circle.position.y = cTrackCenter.y;
circle.position.z = cTrackCenter.z;
scene.add( circle );
// C track curved Inside edge
var geometry = new THREE.CircleBufferGeometry( r-w, 32 );
var circle = new THREE.Mesh( geometry, material );
circle.position.x = cTrackCenter.x;
circle.position.y = cTrackCenter.y;
circle.position.z = cTrackCenter.z;
scene.add( circle );
// C track curved Centerline
var geometry = new THREE.CircleBufferGeometry(r, 32 );
var circle = new THREE.Mesh( geometry, material );
circle.position.x = cTrackCenter.x;
circle.position.y = cTrackCenter.y;
circle.position.z = cTrackCenter.z;
scene.add( circle );
// C track straight section outline - and the C track Zero mark
var geometry = new THREE.Geometry();
geometry.vertices.push new THREE.Vector3( 0, r+w/2, 0 ) ;
geometry.vertices.push new THREE.Vector3( 2r, r+w/2, 0 ) ;
geometry.vertices.push new THREE.Vector3( 2r, r-w/2, 0 ) ;
geometry.vertices.push new THREE.Vector3( 0, r-w/2, 0 ) ;
geometry.vertices.push new THREE.Vector3( 0, r+w/2, 0) ;
var line = new THREE.Line( geometry, material );
scene.add( line );
// C track straight section centerline
var geometry = new THREE.Geometry();
geometry.vertices.push new THREE.Vector3( 0, r, 0 ) ;
geometry.vertices.push new THREE.Vector3( 2r, r, 0 ) ;
var line = new THREE.Line( geometry, material );
scene.add( line );
// C track One Marker
var geometry = new THREE.Geometry();
geometry.vertices.push new THREE.Vector3( 3r-w/2, 2r, 0 ) ;
geometry.vertices.push new THREE.Vector3( 3r-w/2, 2r, 0 ) ;
var line = new THREE.Line( geometry, material );
scene.add( line );
// C track Two Marker
var geometry = new THREE.Geometry();
geometry.vertices.push new THREE.Vector3( 2r, 3r+w/2, 0 ) ;
geometry.vertices.push new THREE.Vector3( 2r, 3r-w/2, 0 ) ;
var line = new THREE.Line( geometry, material );
scene.add( line );
// C track Three Marker
var geometry = new THREE.Geometry();
geometry.vertices.push new THREE.Vector3( r-w/2, 2r, 0 ) ;
geometry.vertices.push new THREE.Vector3( r+w/2, 2r, 0 ) ;
var line = new THREE.Line( geometry, material );
scene.add( line );
// S track centerline
var geometry = new THREE.Geometry();
geometry.vertices.push new THREE.Vector3( 0, r-q, 0 ) ;
geometry.vertices.push new THREE.Vector3( 10r, r-q, 0 ) ;
var line = new THREE.Line( geometry, material );
scene.add( line );
// S track outline
var geometry = new THREE.Geometry();
geometry.vertices.push new THREE.Vector3( 0, r-q+w/2, 0 ) ;
geometry.vertices.push new THREE.Vector3( 10r, r-q+w/2, 0 ) ;
geometry.vertices.push new THREE.Vector3( 10r, r-q-w/2, 0 ) ;
geometry.vertices.push new THREE.Vector3( 0, r-q-w/2, 0 ) ;
geometry.vertices.push new THREE.Vector3( 0, r-q+w/2, 0 ) ;
var line = new THREE.Line( geometry, material );
scene.add( line );
// S track NegOne marker // Made during S track outline
// var geometry = new THREE.Geometry();
// geometry.vertices.push(new THREE.Vector3( 0, r-q+w/2, 0 );
// geometry.vertices.push(new THREE.Vector3( 0, r-q-w/2, 0 );
// var line = new THREE.Line( geometry, material );
// scene.add( line );
// S track Zero marker
var geometry = new THREE.Geometry();
geometry.vertices.push new THREE.Vector3( 2r, r-q+w/2, 0 ) ;
geometry.vertices.push new THREE.Vector3( 2r, r-q-w/2, 0 ) ;
var line = new THREE.Line( geometry, material );
// S track One marker
var geometry = new THREE.Geometry();
geometry.vertices.push new THREE.Vector3( 4r, r-q+w/2, 0 );
geometry.vertices.push new THREE.Vector3( 4r, r-q-w/2, 0 );
var line = new THREE.Line( geometry, material );
scene.add( line );
// S track Two marker
var geometry = new THREE.Geometry();
geometry.vertices.push new THREE.Vector3( 6r, r-q+w/2, 0 );
geometry.vertices.push new THREE.Vector3( 6r, r-q-w/2, 0 );
var line = new THREE.Line( geometry, material );
scene.add( line );
// S track Three marker
var geometry = new THREE.Geometry();
geometry.vertices.push(new THREE.Vector3( 8r, r-q+w/2, 0 ) ;
geometry.vertices.push(new THREE.Vector3( 8r, r-q-w/2, 0 ) ;
var line = new THREE.Line( geometry, material );
scene.add( line );
// S track PI marker
var geometry = new THREE.Geometry();
geometry.vertices.push new THREE.Vector3( 8r + (Math.PI - 3)*2, r-q+w/2, 0) ;
geometry.vertices.push new THREE.Vector3( 8r + (Math.PI - 3)*2, r-q-w/2, 0) ;
var line = new THREE.Line( geometry, material );
scene.add( line );
// S track Four marker // Made during S track outline
// var geometry = new THREE.Geometry();
// geometry.vertices.push new THREE.Vector3( 10r, r-q+w/2, 0 );
// geometry.vertices.push new THREE.Vector3( 10r, r-q-w/2, 0 );
// var line = new THREE.Line( geometry, material );
// scene.add( line );
P.S. Made a few corrections to the code, most important - the function now uses line material instead of mesh.
P.P.S. Haven't run the code but I cleaned up many typos. 14 Sept 0741
.
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
 Re: Animate the PI = 4 experiment
Re: Animate the PI = 4 experiment
.

Much better. I ran the code, made many corrections and observed that the following creates the 'correct' track layout shown above.

Much better. I ran the code, made many corrections and observed that the following creates the 'correct' track layout shown above.
- Code:
function init() {
camera = new THREE.PerspectiveCamera( 70, window.innerWidth / window.innerHeight, 1, 1000 );
camera.position.x = 5;
camera.position.y = 1;
camera.position.z = 5;
scene = new THREE.Scene();
var material = new THREE.LineBasicMaterial( { color: 'yellow' } );
var MAT_LINE_CP = new THREE.LineBasicMaterial( { color: 0x00cc00, linewidth: 0.25 } );
var r = 1;
var w = 0.1 * r; // track width
var q = 0.5 * r; // track separation
var cTrackCenter = new THREE.Vector3( 2*r, 2*r, 0 ) ;
// C track curved Inside edge
for(th=1;th<=360;th+=1)
{
configRadius = r - w/2;
var radians1 = (Math.PI/180) * th;
var radians2 = (Math.PI/180) * (th + 1);
if (th === 359) { radians2 = (Math.PI/180) }
var XYPlaneLine = new THREE.Geometry();
XYPlaneLine.vertices.push( //viewing x and y.
new THREE.Vector3( configRadius * Math.cos(radians1) + cTrackCenter.x, configRadius*Math.sin(radians1)+ cTrackCenter.y, 0 ),
new THREE.Vector3( configRadius * Math.cos(radians2) + cTrackCenter.x, configRadius*Math.sin(radians2) + cTrackCenter.y, 0 ));
var XYLine = new THREE.Line( XYPlaneLine, MAT_LINE_CP);
scene.add(XYLine);
};
// C track curved centerline
for(th=1;th<=360;th+=1)
{
configRadius = r;
var radians1 = (Math.PI/180) * th;
var radians2 = (Math.PI/180) * (th + 1);
if (th === 359) { radians2 = (Math.PI/180) }
var XYPlaneLine = new THREE.Geometry();
XYPlaneLine.vertices.push( //viewing x and y.
new THREE.Vector3( configRadius * Math.cos(radians1) + cTrackCenter.x, configRadius*Math.sin(radians1) + cTrackCenter.y, 0 ),
new THREE.Vector3( configRadius * Math.cos(radians2) + cTrackCenter.x, configRadius*Math.sin(radians2) + cTrackCenter.y, 0 ));
var XYLine = new THREE.Line( XYPlaneLine, MAT_LINE_CP);
scene.add(XYLine);
};
// C track curved outside edge
for(th=1;th<=360;th+=1)
{
configRadius = r + w/2;
var radians1 = (Math.PI/180) * th;
var radians2 = (Math.PI/180) * (th + 1);
if (th === 359) { radians2 = (Math.PI/180) }
var XYPlaneLine = new THREE.Geometry();
XYPlaneLine.vertices.push( //viewing x and y.
new THREE.Vector3( configRadius * Math.cos(radians1) + cTrackCenter.x, configRadius*Math.sin(radians1) + cTrackCenter.y, 0 ),
new THREE.Vector3( configRadius * Math.cos(radians2) + cTrackCenter.x, configRadius*Math.sin(radians2) + cTrackCenter.y, 0 ));
var XYLine = new THREE.Line( XYPlaneLine, MAT_LINE_CP);
scene.add(XYLine);
};
// C track straight section outline - and the C track Zero mark
var geometry = new THREE.Geometry( 1, 1, 1 );
geometry.vertices.push(new THREE.Vector3( 0, r+w/2, 0 ) );
geometry.vertices.push(new THREE.Vector3( 2*r, r+w/2, 0 ) );
geometry.vertices.push(new THREE.Vector3( 2*r, r-w/2, 0 ) );
geometry.vertices.push(new THREE.Vector3( 0, r-w/2, 0 ) );
geometry.vertices.push(new THREE.Vector3( 0, r+w/2, 0 ) );
var line = new THREE.Line( geometry, MAT_LINE_CP );
scene.add( line );
// C track straight section centerline
var geometry = new THREE.Geometry( 1, 1, 1 );
geometry.vertices.push(new THREE.Vector3( 0, r, 0 ) );
geometry.vertices.push(new THREE.Vector3( 2*r, r, 0 ) );
var line = new THREE.Line( geometry, MAT_LINE_CP );
scene.add( line );
// C track One Marker
var geometry = new THREE.Geometry( 1, 1, 1 );
geometry.vertices.push(new THREE.Vector3( 3*r-w/2, 2*r, 0 ) );
geometry.vertices.push(new THREE.Vector3( 3*r+w/2, 2*r, 0 ) );
var line = new THREE.Line( geometry, material );
scene.add( line );
// C track Two Marker
var geometry = new THREE.Geometry( 1, 1, 1 );
geometry.vertices.push(new THREE.Vector3( 2*r, 3*r+w/2, 0 ) );
geometry.vertices.push(new THREE.Vector3( 2*r, 3*r-w/2, 0 ) );
var line = new THREE.Line( geometry, material );
scene.add( line );
// C track Three Marker
var geometry = new THREE.Geometry( 1, 1, 1 );
geometry.vertices.push(new THREE.Vector3( r-w/2, 2*r, 0 ) );
geometry.vertices.push(new THREE.Vector3( r+w/2, 2*r, 0 ) );
var line = new THREE.Line( geometry, material );
scene.add( line );
// S track centerline
var geometry = new THREE.Geometry( 1, 1, 1 );
geometry.vertices.push(new THREE.Vector3( 0, r-q, 0 ) );
geometry.vertices.push(new THREE.Vector3( 10*r, r-q, 0 ) );
var line = new THREE.Line( geometry, MAT_LINE_CP );
scene.add( line );
// S track outline
var geometry = new THREE.Geometry( 1, 1, 1 );
geometry.vertices.push(new THREE.Vector3( 0, r-q+w/2, 0 ) );
geometry.vertices.push(new THREE.Vector3( 10*r, r-q+w/2, 0 ) );
geometry.vertices.push(new THREE.Vector3( 10*r, r-q-w/2, 0 ) );
geometry.vertices.push(new THREE.Vector3( 0, r-q-w/2, 0 ) );
geometry.vertices.push(new THREE.Vector3( 0, r-q+w/2, 0 ) );
var line = new THREE.Line( geometry, MAT_LINE_CP );
scene.add( line );
// S track Zero marker
var geometry = new THREE.Geometry( 1, 1, 1 );
geometry.vertices.push(new THREE.Vector3( 2*r, r-q+w/2, 0 ) );
geometry.vertices.push(new THREE.Vector3( 2*r, r-q-w/2, 0 ) );
var line = new THREE.Line( geometry, material );
scene.add( line );
// S track One marker
var geometry = new THREE.Geometry( 1, 1, 1 );
geometry.vertices.push(new THREE.Vector3( 4*r, r-q+w/2, 0 ) );
geometry.vertices.push(new THREE.Vector3( 4*r, r-q-w/2, 0 ) );
var line = new THREE.Line( geometry, material );
scene.add( line );
// S track Two marker
var geometry = new THREE.Geometry( 1, 1, 1 );
geometry.vertices.push(new THREE.Vector3( 6*r, r-q+w/2, 0 ) );
geometry.vertices.push(new THREE.Vector3( 6*r, r-q-w/2, 0 ) );
var line = new THREE.Line( geometry, material );
scene.add( line );
// S track Three marker
var geometry = new THREE.Geometry( 1, 1, 1 );
geometry.vertices.push(new THREE.Vector3( 8*r, r-q+w/2, 0 ) );
geometry.vertices.push(new THREE.Vector3( 8*r, r-q-w/2, 0 ) );
var line = new THREE.Line( geometry, material );
scene.add( line );
// S track PI marker
var geometry = new THREE.Geometry( 1, 1, 1 );
geometry.vertices.push(new THREE.Vector3( 8*r + (Math.PI - 3)*2, r-q+w/2, 0) );
geometry.vertices.push(new THREE.Vector3( 8*r + (Math.PI - 3)*2, r-q-w/2, 0) );
var line = new THREE.Line( geometry, material );
scene.add( line );
renderer = new THREE.WebGLRenderer();
renderer.setPixelRatio( window.devicePixelRatio );
renderer.setSize( window.innerWidth, window.innerHeight );
document.body.appendChild( renderer.domElement );
window.addEventListener( 'resize', onWindowResize, false );
}
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
 Re: Animate the PI = 4 experiment
Re: Animate the PI = 4 experiment
.
Additional code changes, including several loops to shorten it. The image is slightly cleaner - too little to post it again - distances are green and markers are yellow. r is changed to 10, confirming the output view remains the same - the camera position is also a function of r.
I'll call it final for the time being, subject of course to your approval/changes/recommendations. Personally, I prefer including a full diameter distance in front of the circular track but I'd have absolutely no problem changing it.
P.S. Maybe I misunderstood the tasking? You asked for me to calculate lengths and I plotted the tracks. I'll add centerline distance calculations next. Should take a few minutes, I'll include it in my next post.
.
Additional code changes, including several loops to shorten it. The image is slightly cleaner - too little to post it again - distances are green and markers are yellow. r is changed to 10, confirming the output view remains the same - the camera position is also a function of r.
I'll call it final for the time being, subject of course to your approval/changes/recommendations. Personally, I prefer including a full diameter distance in front of the circular track but I'd have absolutely no problem changing it.
- Code:
function init() {
var r = 10; // Confirming that when r is changed the output view remains the same.
camera = new THREE.PerspectiveCamera( 70, window.innerWidth / window.innerHeight, 1, 1000 );
camera.position.set( 5*r, r, 5*r );
scene = new THREE.Scene();
var material = new THREE.LineBasicMaterial( { color: 'yellow' } ); // markers
var MAT_LINE_CP = new THREE.LineBasicMaterial( { color: 0x00cc00, linewidth: 0.25 } ); // distances
var w = 0.1 * r; // track width
var q = 0.5 * r; // track separation
var cTrackCenter = new THREE.Vector3( 2*r, 2*r, 0 ) ;
// C track circle curve distances: Inside, Centerline, Outside
for(th=1;th<=360;th+=1) {
var radians1 = (Math.PI/180) * th;
var radians2 = (Math.PI/180) * (th + 1);
if (th === 359) { radians2 = (Math.PI/180) }
for ( i = -1; i < 2; i++ ) {
configRadius = r + i*w/2;
var XYPlaneLine = new THREE.Geometry();
XYPlaneLine.vertices.push( //viewing x and y.
new THREE.Vector3( configRadius * Math.cos(radians1) + cTrackCenter.x, configRadius*Math.sin(radians1) + cTrackCenter.y, 0 ),
new THREE.Vector3( configRadius * Math.cos(radians2) + cTrackCenter.x, configRadius*Math.sin(radians2) + cTrackCenter.y, 0 ));
var XYLine = new THREE.Line( XYPlaneLine, MAT_LINE_CP);
scene.add(XYLine);
};
};
// S track markers
var geometry = new THREE.Geometry( 1, 1, 1 );
geometry.vertices.push(new THREE.Vector3( 8*r + r*(Math.PI - 3)*2, r-q+w/2, 0) );
geometry.vertices.push(new THREE.Vector3( 8*r + r*(Math.PI - 3)*2, r-q-w/2, 0) );
var line = new THREE.Line( geometry, material );
scene.add( line ); // PI marker
for ( j = 0; j < 6; j++ ) {
var geometry = new THREE.Geometry( 1, 1, 1 );
geometry.vertices.push(new THREE.Vector3( 2*r*j, r-q+w/2, 0 ) );
geometry.vertices.push(new THREE.Vector3( 2*r*j, r-q-w/2, 0 ) );
var line = new THREE.Line( geometry, material );
scene.add( line ); // Section markers
};
// C track straight section markers
for ( m = 0; m < 2; m++ ) {
var geometry = new THREE.Geometry( 1, 1, 1 );
geometry.vertices.push(new THREE.Vector3( 2*r*m, r+w/2, 0 ) );
geometry.vertices.push(new THREE.Vector3( 2*r*m, r-w/2, 0 ) );
var line = new THREE.Line( geometry, material );
scene.add( line );
};
for ( k = -1; k < 2; k++ ) {
// S track lengths: top edge, centerline and bottom edge
var geometry = new THREE.Geometry( 1, 1, 1 );
geometry.vertices.push(new THREE.Vector3( 0, r-q+k*w/2, 0 ) );
geometry.vertices.push(new THREE.Vector3( 10*r, r-q+k*w/2, 0 ) );
var line = new THREE.Line( geometry, MAT_LINE_CP );
scene.add( line );
// C track lengths: top edge, centerline and bottom edge
var geometry = new THREE.Geometry( 1, 1, 1 );
geometry.vertices.push(new THREE.Vector3( 0, r+k*w/2, 0 ) );
geometry.vertices.push(new THREE.Vector3( 2*r, r+k*w/2, 0 ) );
var line = new THREE.Line( geometry, MAT_LINE_CP );
scene.add( line );
};
// C track markers
var geometry = new THREE.Geometry( 1, 1, 1 );
geometry.vertices.push(new THREE.Vector3( 3*r-w/2, 2*r, 0 ) );
geometry.vertices.push(new THREE.Vector3( 3*r+w/2, 2*r, 0 ) );
var line = new THREE.Line( geometry, material );
scene.add( line ); // C track One Marker
var geometry = new THREE.Geometry( 1, 1, 1 );
geometry.vertices.push(new THREE.Vector3( 2*r, 3*r+w/2, 0 ) );
geometry.vertices.push(new THREE.Vector3( 2*r, 3*r-w/2, 0 ) );
var line = new THREE.Line( geometry, material );
scene.add( line ); // C track Two Marker
var geometry = new THREE.Geometry( 1, 1, 1 );
geometry.vertices.push(new THREE.Vector3( r-w/2, 2*r, 0 ) );
geometry.vertices.push(new THREE.Vector3( r+w/2, 2*r, 0 ) );
var line = new THREE.Line( geometry, material );
scene.add( line ); // C track Three Marker
renderer = new THREE.WebGLRenderer();
renderer.setPixelRatio( window.devicePixelRatio );
renderer.setSize( window.innerWidth, window.innerHeight );
document.body.appendChild( renderer.domElement );
window.addEventListener( 'resize', onWindowResize, false );
};
P.S. Maybe I misunderstood the tasking? You asked for me to calculate lengths and I plotted the tracks. I'll add centerline distance calculations next. Should take a few minutes, I'll include it in my next post.
.
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
 Re: Animate the PI = 4 experiment
Re: Animate the PI = 4 experiment
Great Layout LTAM!
Just a quick question on this...do you think the Manhattan Metric/distance works at the atomic level or photon level with the rolling ball?
https://en.wikipedia.org/wiki/Taxicab_geometry
Just a quick question on this...do you think the Manhattan Metric/distance works at the atomic level or photon level with the rolling ball?
https://en.wikipedia.org/wiki/Taxicab_geometry
 Re: Animate the PI = 4 experiment
Re: Animate the PI = 4 experiment
.
1. Omit the final r, changing to: PI(k) = Circumference/Diameter = 8r/2r = 4
2. Under that line add a new line: The circle distance traveled = 8r.
The first is a whiteout change, and the second would make it more explicit that the circumference traveled around the circular curve is 8r.
Miles identified the kinematics. StevenO came up with the PI = 4 diagram. Nevyn suggested it be scaled to r. Except for my mistakes I can’t claim much credit. In any case, I like it. Seeing the un-fixed variable r causes my mind to wander the scales trying to fix it.
At that smallest scale, I believe spin stacking occurs because of circular motion bucking against the light speed limit. I know that Nevyn has studied this subject - Angular velocity - The spin/circular motions of stacked-spin photons. Please see
Spin Velocity by Steven Smith.
https://www.nevyns-lab.com/mathis/papers/spin-velocity.html
I see Nevyn’s request in light of that paper – which, come to think of it, I should re-read.
I'm sure I wasn't the only one happy to read the raft of new Mile’s papers/updates over the weekend.
One typo (?), from
Faraday and the Arago Effect
.
Thanks for the feedback Cr6. I've lost my objectivity. Fresh eyes, first thing I see looking at it are errors. My next change will be:Great Layout LTAM!
1. Omit the final r, changing to: PI(k) = Circumference/Diameter = 8r/2r = 4
2. Under that line add a new line: The circle distance traveled = 8r.
The first is a whiteout change, and the second would make it more explicit that the circumference traveled around the circular curve is 8r.
Miles identified the kinematics. StevenO came up with the PI = 4 diagram. Nevyn suggested it be scaled to r. Except for my mistakes I can’t claim much credit. In any case, I like it. Seeing the un-fixed variable r causes my mind to wander the scales trying to fix it.
I believe so, absolutely. That’s the point, circular motion applies at any scale. The only limit I see is the scale of the field of motion, the photon field. The photon has a radius and travels at light speed, there is no ‘circular motion’ smaller than a photon.Just a quick question on this...do you think the Manhattan Metric/distance works at the atomic level or photon level with the rolling ball?
At that smallest scale, I believe spin stacking occurs because of circular motion bucking against the light speed limit. I know that Nevyn has studied this subject - Angular velocity - The spin/circular motions of stacked-spin photons. Please see
Spin Velocity by Steven Smith.
https://www.nevyns-lab.com/mathis/papers/spin-velocity.html
I see Nevyn’s request in light of that paper – which, come to think of it, I should re-read.
I'm sure I wasn't the only one happy to read the raft of new Mile’s papers/updates over the weekend.
One typo (?), from
Faraday and the Arago Effect
Isn't the Photon radius around 10E-27m?We can forgive Arago and Faraday for misunderstanding this, since although the charge field is extremely powerful, it is also extremely tenuous in a way, being made up of particles with radii on the scale of 10-37 m.
.
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
 Re: Animate the PI = 4 experiment
Re: Animate the PI = 4 experiment
Airman, I did only expect you to calculate the track lengths, not actually render them, but it is fine to do so and a good way to check that it is working. However, you will need to separate those out. What we need is a middle-man. Something that holds the data without actually doing anything with it. We need that middle-man, the Model, to fit the needs of the View and Controller. Essentially, we need the Model to support the application. That is, we need to use the data in the Model to determine things about the system.
So I suggest you re-write this into 2 or 3 separate functions. The first (and maybe second) will just calculate the track lengths, and the other will use that to create the track objects for rendering.
The middle-man, or Model, will just be an array at the moment. We can formalize it later. Each item in the array will be an object that has 2 properties: type; and length. So the results of the first function will be an array that looks like this:
I replaced length with radius in the curved segment. We may actually need the length as well so feel free to add it in, but keep the radius. We need to be explicit here though. We need to know what that length means. Is it using PIg or PIk? I can find arguments for either, but I think it probably should be PIk.
We actually need 2 tracks, so you could implement them in 2 different functions. You could also wrap the above array in another array that contains both tracks, but I think the nesting is getting a little too troublesome if you do that. It is probably better to keep them separated.
The other function will take that array and create the 3D objects to represent it. This should make that code cleaner since it doesn't need to be wrapped up with the length calculations. Note that this single function will be able to create 3D objects for both segments arrays. We do not need 2 view functions.
So you might end up with something like this:
So I suggest you re-write this into 2 or 3 separate functions. The first (and maybe second) will just calculate the track lengths, and the other will use that to create the track objects for rendering.
The middle-man, or Model, will just be an array at the moment. We can formalize it later. Each item in the array will be an object that has 2 properties: type; and length. So the results of the first function will be an array that looks like this:
- Code:
var segments = [
{ type="straight", length: 10 },
{ type="curve", radius: 3 },
{ type="straight", length: 40 },
];
I replaced length with radius in the curved segment. We may actually need the length as well so feel free to add it in, but keep the radius. We need to be explicit here though. We need to know what that length means. Is it using PIg or PIk? I can find arguments for either, but I think it probably should be PIk.
We actually need 2 tracks, so you could implement them in 2 different functions. You could also wrap the above array in another array that contains both tracks, but I think the nesting is getting a little too troublesome if you do that. It is probably better to keep them separated.
The other function will take that array and create the 3D objects to represent it. This should make that code cleaner since it doesn't need to be wrapped up with the length calculations. Note that this single function will be able to create 3D objects for both segments arrays. We do not need 2 view functions.
So you might end up with something like this:
- Code:
function createStraightTrack( radius )
{
...
}
function createCurvedTrack( radius )
{
...
}
function create3DTrack( segments )
{
...
}
 Re: Animate the PI = 4 experiment
Re: Animate the PI = 4 experiment
Cr6 wrote:Just a quick question on this...do you think the Manhattan Metric/distance works at the atomic level or photon level with the rolling ball?
This is a good question, and one I thought was a simple answer until I gave it a bit more thought.
My first answer was going to be that the object is irrelevant. Only the situation matters. Is it a geometric situation, or is it a kinematic one? Is motion involved? Then it is kinematic.
However, as I put on my philosophers hat, I realise that you could mean: is it the ball that experiences the difference, or is it the atoms, or even photons, that make up the ball that experience it?
My answer remains the same, though. It is the situation that matters. It is the ball that experiences this particular difference. The atoms, or more precisely the photons, do experience their own PIk moments, but they have nothing to do with this one. They are separate problems.
 Re: Animate the PI = 4 experiment
Re: Animate the PI = 4 experiment
.
Copy Nevyn, I'll post my final changes before I read and attempt to follow your instructions.

Latest changes:
1. (0,0) is moved to the center of the circular track in both the code and diagram, making it clear the track radius is r, the PI(g) marker is at the 2PI(g)r and the straight track length is 8r.
2. Added distance w between the two tracks, preventing the two tracks from overlapping.
Copy Nevyn, I'll post my final changes before I read and attempt to follow your instructions.

Latest changes:
1. (0,0) is moved to the center of the circular track in both the code and diagram, making it clear the track radius is r, the PI(g) marker is at the 2PI(g)r and the straight track length is 8r.
2. Added distance w between the two tracks, preventing the two tracks from overlapping.
- Code:
function init() {
var r = 1;
camera = new THREE.PerspectiveCamera( 70, window.innerWidth / window.innerHeight, 1, 1000 );
camera.position.set( 3*r, -r, 5*r );
scene = new THREE.Scene();
var material = new THREE.LineBasicMaterial( { color: 'yellow' } ); // markers
var MAT_LINE_CP = new THREE.LineBasicMaterial( { color: 0x00cc00, linewidth: 0.25 } ); // distances
var w = 0.1 * r; // track width
var q = .05; // track separation
var cTrackCenter = new THREE.Vector3( 0, 0, 0 ) ;
// C track circle curve distances: Inside, Centerline, Outside edge
for(th=1;th<=360;th+=1) {
var radians1 = (Math.PI/180) * th;
var radians2 = (Math.PI/180) * (th + 1);
if (th === 359) { radians2 = (Math.PI/180) }
for ( i = -1; i < 2; i++ ) {
configRadius = r + i*w/2;
var XYPlaneLine = new THREE.Geometry();
XYPlaneLine.vertices.push( //viewing x and y.
new THREE.Vector3( configRadius * Math.cos(radians1) + cTrackCenter.x, configRadius*Math.sin(radians1) + cTrackCenter.y, 0 ),
new THREE.Vector3( configRadius * Math.cos(radians2) + cTrackCenter.x, configRadius*Math.sin(radians2) + cTrackCenter.y, 0 ));
var XYLine = new THREE.Line( XYPlaneLine, MAT_LINE_CP);
scene.add(XYLine);
};
};
// S track markers
var geometry = new THREE.Geometry( 1, 1, 1 );
geometry.vertices.push(new THREE.Vector3( 2*r*Math.PI, -r-q-w/2, 0 ) );
geometry.vertices.push(new THREE.Vector3( 2*r*Math.PI, -r-q-1.5*w, 0 ) );
var line = new THREE.Line( geometry, material );
scene.add( line ); // PI marker
for ( j = 0; j < 6; j++ ) {
var geometry = new THREE.Geometry( 1, 1, 1 );
geometry.vertices.push(new THREE.Vector3( -2*r+2*r*j, -r-q-w/2, 0 ) );
geometry.vertices.push(new THREE.Vector3( -2*r+2*r*j, -r-q-1.5*w, 0 ) );
var line = new THREE.Line( geometry, material );
scene.add( line ); // Section markers
}
// C track straight section markers
for ( m = 0; m < 2; m++ ) {
var geometry = new THREE.Geometry( 1, 1, 1 );
geometry.vertices.push(new THREE.Vector3( -2*r+2*r*m, -r+w/2, 0 ) );
geometry.vertices.push(new THREE.Vector3( -2*r+2*r*m, -r-w/2, 0 ) );
var line = new THREE.Line( geometry, material );
scene.add( line );
}
for ( k = -1; k < 2; k++ ) {
// S track lengths: top edge, centerline and bottom edge
var geometry = new THREE.Geometry( 1, 1, 1 );
geometry.vertices.push(new THREE.Vector3( -2*r, -r-w-q+k*w/2, 0 ) );
geometry.vertices.push(new THREE.Vector3( 8*r, -r-w-q+k*w/2, 0 ) );
var line = new THREE.Line( geometry, MAT_LINE_CP );
scene.add( line );
// C track lengths: top edge, centerline and bottom edge
var geometry = new THREE.Geometry( 1, 1, 1 );
geometry.vertices.push(new THREE.Vector3( -2*r, -r+k*w/2, 0 ) );
geometry.vertices.push(new THREE.Vector3( 0, -r+k*w/2, 0 ) );
var line = new THREE.Line( geometry, MAT_LINE_CP );
scene.add( line );
}
// C track markers
var geometry = new THREE.Geometry( 1, 1, 1 );
geometry.vertices.push(new THREE.Vector3( r-w/2, 0, 0 ) );
geometry.vertices.push(new THREE.Vector3( r+w/2, 0, 0 ) );
var line = new THREE.Line( geometry, material );
scene.add( line ); // C track One Marker
var geometry = new THREE.Geometry( 1, 1, 1 );
geometry.vertices.push(new THREE.Vector3( 0, r+w/2, 0 ) );
geometry.vertices.push(new THREE.Vector3( 0, r-w/2, 0 ) );
var line = new THREE.Line( geometry, material );
scene.add( line ); // C track Two Marker
var geometry = new THREE.Geometry( 1, 1, 1 );
geometry.vertices.push(new THREE.Vector3( -r-w/2, 0, 0 ) );
geometry.vertices.push(new THREE.Vector3( -r+w/2, 0, 0 ) );
var line = new THREE.Line( geometry, material );
scene.add( line ); // C track Three Marker
renderer = new THREE.WebGLRenderer();
renderer.setPixelRatio( window.devicePixelRatio );
renderer.setSize( window.innerWidth, window.innerHeight );
document.body.appendChild( renderer.domElement );
window.addEventListener( 'resize', onWindowResize, false );
}
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
 Re: Animate the PI = 4 experiment
Re: Animate the PI = 4 experiment
.
If I follow you instructions correctly, these 6 arrays contain all the track model data. Would the work? I included a naming convention to make drawing arcs and line segments easy. Feel free to straighten or curve as necessary.
PI = 4 Track Layout coordinates, segments and distance markers - the model data.
There are two track types (C)urved and (S)traight, and three data arrays per track, six total :cCoorinates, cSegments, cMarkers, sCoorinates, sSegments, sMarkers
Coordinates. cCoordinates and sCoordinates contain all C or S track coordinates as a function of r.
Segments. Lists all the track's forward Line segments. The track total length is dived into 5 sections for the curved track,(1 straight and 4 curved) and 6 sections for the straight track; the PI(g) marker is treated as a short section of the S track length. The segments are named by their coordinate named endpoints and type. In effect, the c or s Segments array provides the plotting instructions for the long parallel (or concentric) track length lines.
Markers. These are the distance markers on the two track, orthogonal to the forward direction. As with the segment arrays, the marker array names include the two track width coordinate edge points.
If I follow you instructions correctly, these 6 arrays contain all the track model data. Would the work? I included a naming convention to make drawing arcs and line segments easy. Feel free to straighten or curve as necessary.
PI = 4 Track Layout coordinates, segments and distance markers - the model data.
There are two track types (C)urved and (S)traight, and three data arrays per track, six total :cCoorinates, cSegments, cMarkers, sCoorinates, sSegments, sMarkers
Coordinates. cCoordinates and sCoordinates contain all C or S track coordinates as a function of r.
Segments. Lists all the track's forward Line segments. The track total length is dived into 5 sections for the curved track,(1 straight and 4 curved) and 6 sections for the straight track; the PI(g) marker is treated as a short section of the S track length. The segments are named by their coordinate named endpoints and type. In effect, the c or s Segments array provides the plotting instructions for the long parallel (or concentric) track length lines.
Markers. These are the distance markers on the two track, orthogonal to the forward direction. As with the segment arrays, the marker array names include the two track width coordinate edge points.
- Code:
// C track coordinates: // For curved C track the suffix: a is the inside curve,
var cCoorinates = [
{ name="c1a", coords=( -2*r, -r+w/2, 0 )},
{ name="c1b", coords=( -2*r, -r, 0 )},
{ name="c1c", coords=( -2*r, -r-w/2, 0 )},
{ name="c2a", coords=( 0, -r+w/2, 0 )},
{ name="c2b", coords=( 0, -r, 0 )},
{ name="c2c", coords=( 0, -r-w/2, 0 )},
{ name="c3a", coords=( r-w/2, 0, 0)},
{ name="c3b", coords=( r, 0, 0 )},
{ name="c3c", coords=( r+w/2, 0, 0 )},
{ name="c4a", coords=( 0, -r+w/2, 0)},
{ name="c4b", coords=( 0, -r, 0 )},
{ name="c4c", coords=( 0, -r-w/2, 0 )},
{ name="c5a", coords=( -r, -r+w/2, 0},
{ name="c5b", coords=( -r, -r, 0 )},
{ name="c5c", coords=( -r, -r-w/2, 0 )}
];
// C track segments
// coordinate endpoints name and type (S(traight) or C(urved)) suffix.
// C track PI(g) Inside, Centerline and Outside curve lengths
var cSegments = [
{ name="c1aC2aS", type="straight", length: 2*r },
{ name="c2aC3aC", type="curve", length: 2*Math.PI*(r-w/2)/4, radius: r-w/2 },
{ name="c3aC4aC", type="curve", length: 2*Math.PI*(r-w/2)/4, radius: r-w/2 },
{ name="c4aC5aC", type="curve", length: 2*Math.PI*(r-w/2)/4, radius: r-w/2 },
{ name="c5aC2aC", type="curve", length: 2*Math.PI*(r-w/2)/4, radius: r-w/2 },
{ name="c1bC2bS", type="straight", length: 2*r },
{ name="c2bC3bC", type="curve", length: 2*Math.PI*r/4, radius: r },
{ name="c3bC4bC", type="curve", length: 2*Math.PI*r/4 , radius: r },
{ name="c4bC5bC", type="curve", length: 2*Math.PI*r/4, radius: r },
{ name="c5bC2bC", type="curve", length: 2*Math.PI*r/4, radius: r },
{ name="c1cC2cS", type="straight", length: 2*r },
{ name="c2cC3cC", type="curve", length: 2*Math.PI*(r+w/2)/4, radius: r+w/2 },
{ name="c3cC4cC", type="curve", length: 2*Math.PI*(r+w/2)/4, radius: r+w/2 },
{ name="c4cC5cC", type="curve", length: 2*Math.PI*(r+w/2)/4, radius: r+w/2 },
{ name="c5cC2cC", type="curve", length: 2*Math.PI*(r+w/2)/4, radius: r+w/2 }
];
// C track Markers //coordinate endpoints name
var cMarkers = [
{ name="c1aC1c", type="straight", length: w },
{ name="c2aC2c", type="straight", length: w },
{ name="c3aC3c", type="straight", length: w },
{ name="c4aC4c", type="straight", length: w },
{ name="c5aC5c", type="straight", length: w }
];
// S track coordinates // For straight S track the suffix: a is the top track edge - closest to the
// circular track. b is the Centerline, and c is the bottom track edge, furthest from the circular track.
var sCoorinates = [
{ name="s1a", coords=( -2*r, -r-q-w/2, 0 )},
{ name="s1b", coords=( -2*r, -r-q-w/2, 0 )},
{ name="s1c", coords=( -2*r, -r-q-3*w/2, 0 )},
{ name="s2a", coords=( 0, -r-q-w/2, 0 )},
{ name="s2b", coords=( 0, -r-q-w, 0)},
{ name="s2c", coords=( 0, -r-q-3*w/2, 0 )},
{ name="s3a", coords=( 2*r, -r-q-w/2, 0 )},
{ name="s3b", coords=( 2*r, -r-q-w, 0 )},
{ name="s3c", coords=( 2*r, -r-q-3*w/2, 0 )},
{ name="s4a", coords=( 4*r, -r-q-w/2, 0 )},
{ name="s4b", coords=( 4*r, -r-q-w, 0 )},
{ name="s4c", coords=( 4*r, -r-q-3*w/2, 0 )},
{ name="s5a", coords=( 6*r, -r-q-w/2, 0 )},
{ name="s5b", coords=( 6*r, -r-q-w, 0 )},
{ name="s5c", coords=( 6*r, -r-q-3*w/2, 0 )},
{ name="s6a", coords=( 2*Math.PI*r, -r-q-w/2, 0 )},
{ name="s6b", coords=( 2*Math.PI*r, -r-q-w, 0 )},
{ name="s6c", coords=( 2*Math.PI*r, -r-q-3*w/2, 0 )},
{ name="s7a", coords=( 8*r, -r-q-w/2, 0 )},
{ name="s7b", coords=( 8*r, -r-q-w, 0 )},
{ name="s7c", coords=( 8*r, -r-q-3*w/2, 0 )}
];
// S track segment, all lines parallel to the track
var sSegments = [
{ name="s1aS2aS", type="straight", length: 2*r },
{ name="s2aS3aS", type="straight", length: 2*r },
{ name="s3aS4a", type="straight", length: 2*r },
{ name="s4aS5aS", type="straight", length: 2*r },
{ name="s5aS6aS", type="straight", length: Math.PI*2*r-6*r },
{ name="s6aS7aS", type="straight", length: 2*r-Math.PI*2*r },
{ name="s1bS2bS", type="straight", length: 2*r },
{ name="s2bS3bS", type="straight", length: 2*r },
{ name="s3bS4b", type="straight", length: 2*r },
{ name="s4bS5bS", type="straight", length: 2*r },
{ name="s5bS6bS", type="straight", length: Math.PI*2*r-6*r },
{ name="s6bS7bS", type="straight", length: 2*r-Math.PI*2*r },
{ name="s1cS2cS", type="straight", length: 2*r },
{ name="s2cS3cS", type="straight", length: 2*r },
{ name="s3cS4c", type="straight", length: 2*r },
{ name="s4cS5cS", type="straight", length: 2*r },
{ name="s5cS6cS", type="straight", length: Math.PI*2*r-6*r },
{ name="s6cS7cS", type="straight", length: 2*r-Math.PI*2*r }
];
// S track Markers, coordinate endpoints name, width lines ortho (side-to-side) to the track's forward direction.
var sMarkers = [
{ name="s1aS1c", type="straight", length: w },
{ name="s2aS2c", type="straight", length: w },
{ name="s3aS3c", type="straight", length: w },
{ name="s4aS4c", type="straight", length: w },
{ name="s5aS5c", type="straight", length: w },
{ name="s6aS6c", type="straight", length: w },
{ name="s7aS7c", type="straight", length: w }
];
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
 Re: Animate the PI = 4 experiment
Re: Animate the PI = 4 experiment
Too much information. You're thinking about the View, while trying to define the Model. Separating them isn't exactly easy, although it does get easier the more you do it. What you need to be thinking is "What is the minimal amount of data that the Model must contain for the View(s) and Controller(s) to function?". The focus must be on the minimal.
You have data for 3 lines per track, but that is a View issue, not a Model one. The track should be a single line that the ball will follow. Probably a center line which the center of the ball will follow. The View, when it sets up the rendering objects, takes that center line and creates the others. Although, I would prefer a tube that is transparent, if we can accomplish that and it looks good. Same for the markers, that is purely a View consideration. The coordinates can also be calculated from the track lengths.
Basically, everything should start in the View or Controller, depending on what you are working on, and be moved to the Model when it is necessary to do so. Some things naturally fit in the Model, even if they are used by the View or Controller, but you get a feel for that with experience.
I know I am asking a lot, but I don't expect you to get it all right on your first try. It is very difficult to separate things like I am asking, especially when you don't have a good idea of what the separate pieces are doing in a specific problem. So let's have a look at that.
While I have described the general idea of MVC, what we need is a specific idea. We need to identify what each piece needs to know and what it wants to do with it.
The Controller is what we really want out of this. This is what will do all of the work, so we should focus on meeting its needs. So what does it need? Well, let's define what it needs to do in order to see what we can give it to do that task.
The Controller is what will move the ball. It will need to interpret the track in order to determine where the ball is on that track. It will need to determine where the ball must move to next. So it is important that the Model accommodate that need. More important than the View. The Controller will be doing most of the work while the system is running.
The View only needs to create the 3D scene and keep it up-to-date with the Model. The View should end up being heavy on initialization, but light on runtime processing. The tracks should be created during init and forgotten about by the View. They are static, although we could do things like highlight the current segment, if we want to (once everything is working). The runtime requirements for the View are just see where the ball currently is and update the 3D scene.
Given that outline, we can see that the View mostly just sets things up and the Controller does most of the work. We need the Controller to be more efficient than the View since it will be working every frame. The View also works every frame, but only updates rather than raw processing. The heavy lifting is done by the Controller.
So the Model should not contain data that the Controller does not need. It is fine for the Model to have data that only the View would need, but it must be justified. Basically, if the View can work it out for itself, then it should. On the other hand, we want to minimise the work that the Controller must perform, so we can adjust the Model to accommodate it.
Note that these last few paragraphs refer to this particular problem. In another app, doing some other job, it might be the View that we want to make efficient and the Controller is not as important. Well, the Controller is usually always important, but sometimes the View can be just as important or even more so. So please don't take this in a general way. Each problem presents its own wants and needs.
How does all of that effect what you have already created? Well, there are too many track segments in the Model. How does the Controller determine which ones it should care about? It doesn't want to know about those inside and outside lines. It only wants to care about the line that the ball must follow. So it should not need to figure that out while it is processing.
We want a simple array where each item is connected to the last. In previous posts I have kept that pretty simple. However, we may end up making it more complex such as storing the start and end coordinate of each track segment because that might make it faster to process. But I don't want that yet. Let's build up what we need, rather than building more than we want.
What you have done is good and still useful. It just needs to be separated and, at least some parts, simplified.
You have data for 3 lines per track, but that is a View issue, not a Model one. The track should be a single line that the ball will follow. Probably a center line which the center of the ball will follow. The View, when it sets up the rendering objects, takes that center line and creates the others. Although, I would prefer a tube that is transparent, if we can accomplish that and it looks good. Same for the markers, that is purely a View consideration. The coordinates can also be calculated from the track lengths.
Basically, everything should start in the View or Controller, depending on what you are working on, and be moved to the Model when it is necessary to do so. Some things naturally fit in the Model, even if they are used by the View or Controller, but you get a feel for that with experience.
I know I am asking a lot, but I don't expect you to get it all right on your first try. It is very difficult to separate things like I am asking, especially when you don't have a good idea of what the separate pieces are doing in a specific problem. So let's have a look at that.
While I have described the general idea of MVC, what we need is a specific idea. We need to identify what each piece needs to know and what it wants to do with it.
The Controller is what we really want out of this. This is what will do all of the work, so we should focus on meeting its needs. So what does it need? Well, let's define what it needs to do in order to see what we can give it to do that task.
The Controller is what will move the ball. It will need to interpret the track in order to determine where the ball is on that track. It will need to determine where the ball must move to next. So it is important that the Model accommodate that need. More important than the View. The Controller will be doing most of the work while the system is running.
The View only needs to create the 3D scene and keep it up-to-date with the Model. The View should end up being heavy on initialization, but light on runtime processing. The tracks should be created during init and forgotten about by the View. They are static, although we could do things like highlight the current segment, if we want to (once everything is working). The runtime requirements for the View are just see where the ball currently is and update the 3D scene.
Given that outline, we can see that the View mostly just sets things up and the Controller does most of the work. We need the Controller to be more efficient than the View since it will be working every frame. The View also works every frame, but only updates rather than raw processing. The heavy lifting is done by the Controller.
So the Model should not contain data that the Controller does not need. It is fine for the Model to have data that only the View would need, but it must be justified. Basically, if the View can work it out for itself, then it should. On the other hand, we want to minimise the work that the Controller must perform, so we can adjust the Model to accommodate it.
Note that these last few paragraphs refer to this particular problem. In another app, doing some other job, it might be the View that we want to make efficient and the Controller is not as important. Well, the Controller is usually always important, but sometimes the View can be just as important or even more so. So please don't take this in a general way. Each problem presents its own wants and needs.
How does all of that effect what you have already created? Well, there are too many track segments in the Model. How does the Controller determine which ones it should care about? It doesn't want to know about those inside and outside lines. It only wants to care about the line that the ball must follow. So it should not need to figure that out while it is processing.
We want a simple array where each item is connected to the last. In previous posts I have kept that pretty simple. However, we may end up making it more complex such as storing the start and end coordinate of each track segment because that might make it faster to process. But I don't want that yet. Let's build up what we need, rather than building more than we want.
What you have done is good and still useful. It just needs to be separated and, at least some parts, simplified.
 Re: Animate the PI = 4 experiment
Re: Animate the PI = 4 experiment
.
PI = 4 Experiment. The Balls’ Curved and Straight paths.
Thanks for the descriptions and guidance - so much clearer than my usual typo type thinking, I believe I understand the gist of it. In this application, the most important details are the balls' paths. The following code contains the two track forward center lines. s6b - the PI(g) distance marker is consigned to the View.
// I realize these arrays are 'in the form', notional for the time being for easy understanding. In order to function properly they need to be reduced
// slightly too, such as.
var sSegments = [
[ "s1bS2bS", "straight", 2*r ],
[ "s2bS3bS", "straight", 2*r ],
[ "s3bS4bS", "straight", 2*r ],
[ "s4bS5bS", "straight", 2*r ],
[ "s5bS7bS", "straight", 2*r ],
];
// Which could be further reduced to
var sSegments = [
[ "s1bS7bS", "straight", 10*r ],
];
// But I don't believe 4 line sections are burdening the Controller. The circular track is broken into four arcs, so let S be 5 line segments(?).
I guess the Ball comes next.
P.S. I had to add a couple of S segment suffixes.
.
PI = 4 Experiment. The Balls’ Curved and Straight paths.
Thanks for the descriptions and guidance - so much clearer than my usual typo type thinking, I believe I understand the gist of it. In this application, the most important details are the balls' paths. The following code contains the two track forward center lines. s6b - the PI(g) distance marker is consigned to the View.
- Code:
///////////////////////////////////////////
// PI = 4 Experiment. The Balls’ Curved and Straight paths.
// C track coordinates:
var cCoordinates = [
{ name="c1b", coords=( -2*r, -r, 0 )},
{ name="c2b", coords=( 0, -r, 0 )},
{ name="c3b", coords=( r, 0, 0 )},
{ name="c4b", coords=( 0, r, 0 )},
{ name="c5b", coords=( -r, 0, 0 )},
];
// C track single line segment and 4 arc segments
// coordinate endpoints name and type (S(traight) or C(urved)) suffix.
// C track center line PI(g) length
var cSegments = [
{ name="c1bC2bS", type="straight", length: 2*r },
{ name="c2bC3bC", type="curve", length: 2*Math.PI*r/4, radius: r },
{ name="c3bC4bC", type="curve", length: 2*Math.PI*r/4 , radius: r },
{ name="c4bC5bC", type="curve", length: 2*Math.PI*r/4, radius: r },
{ name="c5bC2bC", type="curve", length: 2*Math.PI*r/4, radius: r },
];
// S track center line coordinates. // s6b - the PI(g) distance marker will be part of the View.
var sCoordinates = [
{ name="s1b", coords=( -2*r, -r-q-w, 0 )},
{ name="s2b", coords=( 0, -r-q-w, 0)},
{ name="s3b", coords=( 2*r, -r-q-w, 0 )},
{ name="s4b", coords=( 4*r, -r-q-w, 0 )},
{ name="s5b", coords=( 6*r, -r-q-w, 0 )},
{ name="s7b", coords=( 8*r, -r-q-w, 0 )},
];
// S track segments, all lines parallel to the track
var sSegments = [
{ name="s1bS2bS", type="straight", length: 2*r },
{ name="s2bS3bS", type="straight", length: 2*r },
{ name="s3bS4bS", type="straight", length: 2*r },
{ name="s4bS5bS", type="straight", length: 2*r },
{ name="s5bS7bS", type="straight", length: 2*r },
];
// I realize these arrays are 'in the form', notional for the time being for easy understanding. In order to function properly they need to be reduced
// slightly too, such as.
var sSegments = [
[ "s1bS2bS", "straight", 2*r ],
[ "s2bS3bS", "straight", 2*r ],
[ "s3bS4bS", "straight", 2*r ],
[ "s4bS5bS", "straight", 2*r ],
[ "s5bS7bS", "straight", 2*r ],
];
// Which could be further reduced to
var sSegments = [
[ "s1bS7bS", "straight", 10*r ],
];
// But I don't believe 4 line sections are burdening the Controller. The circular track is broken into four arcs, so let S be 5 line segments(?).
I guess the Ball comes next.
P.S. I had to add a couple of S segment suffixes.
.
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
 Re: Animate the PI = 4 experiment
Re: Animate the PI = 4 experiment
.

NOT a draft final - Testing only.
I added two balls of radius w/2 to the track starting positions (in the init function). The animate function I include below directs them through their tracks. The two ball cross their marks close to the same time. The image shows the straight ball is slightly behind the curved. They cross their final 4r markers and are back at and past their starting positions without a pause.
This is neither a draft final nor desired product. There is no keyframing; no time checking; they are on an infinite loop, they soon drift apart. I had to try, and was happy to find I could add the linear and rotation animations without too much difficulty.

NOT a draft final - Testing only.
I added two balls of radius w/2 to the track starting positions (in the init function). The animate function I include below directs them through their tracks. The two ball cross their marks close to the same time. The image shows the straight ball is slightly behind the curved. They cross their final 4r markers and are back at and past their starting positions without a pause.
This is neither a draft final nor desired product. There is no keyframing; no time checking; they are on an infinite loop, they soon drift apart. I had to try, and was happy to find I could add the linear and rotation animations without too much difficulty.
- Code:
function animate() {
requestAnimationFrame( animate );
sphereC.position.x += 0.32;
distL += 0.25;
if ( (sphereC.position.x > 0) && ( sphereC.position.y = -r )){
inLoop = true;
};
if ( inLoop ) {
inLCounter += 1;
currentAngle += 0.004; //
rotation = currentAngle * Math.PI;
sphereC.position.y = -r*Math.cos(rotation);
sphereC.position.x = r*Math.sin(rotation);
};
if ( (sphereC.position.x > 0) && ( inLCounter > 500 )) {
sphereC.position.set( -2*r, -r, 0 );
inLoop = false ;
inLCounter = 0 ;
};
sphereS.position.x += 0.32;
if ( sphereS.position.x > 8*r ){
sphereS.position.set( -2*r, -r-q-w, 0 );
};
renderer.render( scene, camera );
}
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
 Re: Animate the PI = 4 experiment
Re: Animate the PI = 4 experiment
.
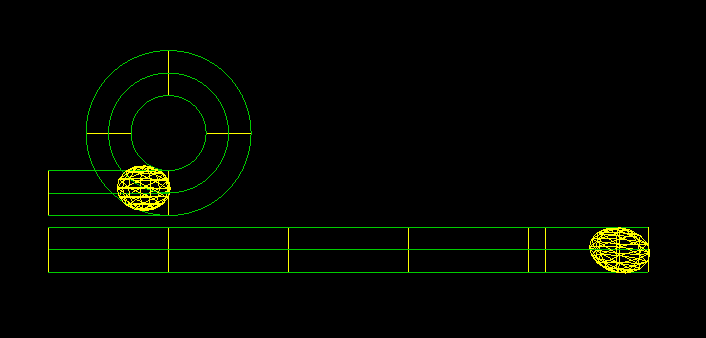
Incremental improvements are in order.
I’m building on yesterday’s results, including rationalizations. For example, all the animation function does is to guide the balls through their tracks; I believe that meets your criteria for 'the Controller'. Fine tuning the animation function seems like a good way to advance my more modest effort. I made the spheres large and wireframe as a necessary pre-requisite to view the attempts of my next intended animation - rolling. Oops, the radius was 20, now it’s back to one. I used the continuous loop, trial and effort, and binary number divisions to come up with roughly equal distances, angular and linear.
var angInc = what I add to the currentAngle the angular position of the ball on the circular track, the angle increment = 0.006;
var forInc = the forward straight increment, x + = 0.0240384618125; // a tiny bit fast
I need a reality check. How are those numbers related? Given the angular addition of 0.006, how can I calculate the corresponding straight segment increment? That’s where I am at the moment.
Feel free to direct me otherwise.
.

Incremental improvements are in order.
I’m building on yesterday’s results, including rationalizations. For example, all the animation function does is to guide the balls through their tracks; I believe that meets your criteria for 'the Controller'. Fine tuning the animation function seems like a good way to advance my more modest effort. I made the spheres large and wireframe as a necessary pre-requisite to view the attempts of my next intended animation - rolling. Oops, the radius was 20, now it’s back to one. I used the continuous loop, trial and effort, and binary number divisions to come up with roughly equal distances, angular and linear.
var angInc = what I add to the currentAngle the angular position of the ball on the circular track, the angle increment = 0.006;
var forInc = the forward straight increment, x + = 0.0240384618125; // a tiny bit fast
I need a reality check. How are those numbers related? Given the angular addition of 0.006, how can I calculate the corresponding straight segment increment? That’s where I am at the moment.
Feel free to direct me otherwise.
.
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
 Re: Animate the PI = 4 experiment
Re: Animate the PI = 4 experiment
If that angle represents the roll of the ball caused by its own motion, then the straight line increment represents the circumference of the ball, so they are related by PI. Which is backed by their mathematical relationship: 0.0240384618125 / 0.006 = 4.0064103020833.
However, that is the wrong PI to use, and that is why it is a bit fast. This calculation should use 3.14 because it is a geometrical calculation. I can't fault you for using PI=4 since you were looking at a ball in motion. I explicitly stated above that if motion is involved then use 4, but I should have been a lot clearer.
When something is in motion and that motion is along a circumference, then you use PI=4 when making calculations about the motion of it.
In this case though, we want to find the straight line distance covered during the same time that the ball has rolled a given angle. Which is just another way of asking for the equivallent straight line distance of the circumference over that angle.
Maybe another way to state the difference in PI's is that PI=3.14 is used for distances, but PI=4 is used for velocities.
So if you are using an equation containing PI and that equation also contains velocities, then it probably needs PI=4. This gets very tricky when an equation contains both distances and velocities, and even more so if you break the velocities down into distances so they are hidden. If there are multiple PI's, then they may actually be different versions of PI, so you may need 3.14 and 4 in the same equation. This is why it is so critical that the math is backed by good theory. Only the theory can tell us where each part comes into the equation and how to ensure that each part is treated correctly.
Here's another way to look at it. PI=3.14 is trying to approximate the circumference. It doesn't care how that circumference came to be, it just wants to know the real length of it. PI=4 is trying to approximate motion along the circumference. It does care about how that motion came to be, because it wants to know the real forces required to move along it.
However, that is the wrong PI to use, and that is why it is a bit fast. This calculation should use 3.14 because it is a geometrical calculation. I can't fault you for using PI=4 since you were looking at a ball in motion. I explicitly stated above that if motion is involved then use 4, but I should have been a lot clearer.
When something is in motion and that motion is along a circumference, then you use PI=4 when making calculations about the motion of it.
In this case though, we want to find the straight line distance covered during the same time that the ball has rolled a given angle. Which is just another way of asking for the equivallent straight line distance of the circumference over that angle.
Maybe another way to state the difference in PI's is that PI=3.14 is used for distances, but PI=4 is used for velocities.
So if you are using an equation containing PI and that equation also contains velocities, then it probably needs PI=4. This gets very tricky when an equation contains both distances and velocities, and even more so if you break the velocities down into distances so they are hidden. If there are multiple PI's, then they may actually be different versions of PI, so you may need 3.14 and 4 in the same equation. This is why it is so critical that the math is backed by good theory. Only the theory can tell us where each part comes into the equation and how to ensure that each part is treated correctly.
Here's another way to look at it. PI=3.14 is trying to approximate the circumference. It doesn't care how that circumference came to be, it just wants to know the real length of it. PI=4 is trying to approximate motion along the circumference. It does care about how that motion came to be, because it wants to know the real forces required to move along it.
 Re: Animate the PI = 4 experiment
Re: Animate the PI = 4 experiment
Hi guys, long time no see. I hope you're well and fine 
Just a few hopefully constructive remarks where I find your wording confusing, following what Miles wrote about differing between a length and a distance:
"A length is a given parameter that does not include motion or time. It is geometric only. But a distance is a length traveled in some real time, so it requires motion. A length is not kinematic, while a distance is. The circumference 2πr is a length. The circumference 8r is a distance."
(http://milesmathis.com/are.html)
On the other hand, velocity is length covered by a moving object over time. This is just to say that distance and velocity both already imply motion / kinematic situation, so Pi=4 would be used to calculate their traveled distance in both cases.
"A static circle and a circle drawn by motion are not the same. The number π works only on the given static circle, in which there is no motion, no time, and no drawing. Any real-world circle drawn in time by a real object cannot be described with π." (http://milesmathis.com/pi2.html
In my own interpretation of all this:

-> a straight line/track is simply the length of circumference of the circle described by the other track; expressed in r(adius). So it implies a static measurement, which should be done with Pi=3,14 when setting up the experiment. In other words, the length of curved path (when straightened out) is measured 21% longer than the length of straight path.
When motion is involved, the length becomes a distance. But there is a big difference between the two paths in the above experiment: one path also involves changing the moving ball's position on both y-axis and x-axis, while the other one is only about the ball's position change along its x-axis. So any distance and/or velocity along the curved path should be calculated using Pi=4 when looking at the moving ball. Such calculation then corresponds to the visual effect of apparent "slowdown" of the ball following the curved path (as noticed in SteveO's YT video) : as the ball moves on both x- and y-axis at the same delta t(ime) while inside the curve, it appears to our eyes as it slowed down, which the math correctly shows as true if we apply Pi=4 for the curved section's calculations of ball's linear velocity. But the slow down is only an illusion: if we calculate delta d(istance) for both x- and y-axis over delta t, and sum them up, we get the same delta d of the other ball moving along the straight path in delta t.
I think this means that the velocity of the ball is accelerated while inside the curve? Which then leads to angular velocity and momentum?
I'm absolutely clueless how to include this properly into the Airman's code...
Just a few hopefully constructive remarks where I find your wording confusing, following what Miles wrote about differing between a length and a distance:
"A length is a given parameter that does not include motion or time. It is geometric only. But a distance is a length traveled in some real time, so it requires motion. A length is not kinematic, while a distance is. The circumference 2πr is a length. The circumference 8r is a distance."
(http://milesmathis.com/are.html)
On the other hand, velocity is length covered by a moving object over time. This is just to say that distance and velocity both already imply motion / kinematic situation, so Pi=4 would be used to calculate their traveled distance in both cases.
"A static circle and a circle drawn by motion are not the same. The number π works only on the given static circle, in which there is no motion, no time, and no drawing. Any real-world circle drawn in time by a real object cannot be described with π." (http://milesmathis.com/pi2.html
In my own interpretation of all this:

-> a straight line/track is simply the length of circumference of the circle described by the other track; expressed in r(adius). So it implies a static measurement, which should be done with Pi=3,14 when setting up the experiment. In other words, the length of curved path (when straightened out) is measured 21% longer than the length of straight path.
When motion is involved, the length becomes a distance. But there is a big difference between the two paths in the above experiment: one path also involves changing the moving ball's position on both y-axis and x-axis, while the other one is only about the ball's position change along its x-axis. So any distance and/or velocity along the curved path should be calculated using Pi=4 when looking at the moving ball. Such calculation then corresponds to the visual effect of apparent "slowdown" of the ball following the curved path (as noticed in SteveO's YT video) : as the ball moves on both x- and y-axis at the same delta t(ime) while inside the curve, it appears to our eyes as it slowed down, which the math correctly shows as true if we apply Pi=4 for the curved section's calculations of ball's linear velocity. But the slow down is only an illusion: if we calculate delta d(istance) for both x- and y-axis over delta t, and sum them up, we get the same delta d of the other ball moving along the straight path in delta t.
I think this means that the velocity of the ball is accelerated while inside the curve? Which then leads to angular velocity and momentum?
I'm absolutely clueless how to include this properly into the Airman's code...
Vexman- Posts : 73
Join date : 2019-02-25
 Re: Animate the PI = 4 experiment
Re: Animate the PI = 4 experiment
.
Hi Vexman. Good to hear from you. Every year or so I keep coming back to PI=4, each time I’ve read Miles’ papers again and think I know the subject, needless to say, I still have plenty to learn.
I corrected a big error in my current angle calculation I’m sure you noticed. I made another ‘correction’, my initial choice of 0.006 as an incremental angle was arbitrary and poor. The total number of increments was between 333 and 334 which made no sense, This time I tried dividing the circle – 2PI rads by 400 (= 0.0157rad) and straight distance 8, by 400 (0.02) .
But that didn’t work. Believe it or not, the PI=4 layout is a lot like an old oscilloscope output display problem. I can synchronize two moving blips along the two tracks by controlling the values of two controls: angle increment and forward increment. Actually I keep var angInc constant and vary var forInc until I arrive at simultaneous tracks, I then look at the values.
var angInc = 0.015707963267949; // 2 PI rad/400
var forInc = 0.0200675; // 0.02 is too slow.
I wish I could explain why I deviate so far from 0.02. I very much enjoy working on such efforts and feel that the only way I can contribute is through dedication and perseverance.
For the time being Nevyn, I can only imagine rolling on the straight track.
.
- Code:
function animate() {
requestAnimationFrame( animate );
var velocity = 1;
var angInc = velocity * 0.015707963267949; // PI rad/200
var forInc = velocity * 0.0200675; //= 0.02; slow // 0.020125; fast
sphereC.position.x += forInc;
if ( (sphereC.position.x > 0) && ( sphereC.position.y = -r )){
inLoop = true;
};
if ( inLoop ) {
inLCounter += 1;
currentAngle += angInc;
sphereC.position.y = -r*Math.cos(currentAngle);
sphereC.position.x = r*Math.sin(currentAngle);
};
if ( (sphereC.position.x > 0) && ( inLCounter > 300 )) {
sphereC.position.set( -2*r, -r, 0 );
console.log( 'inLCounter = '+ inLCounter +'.'); // inLCounter for the loop equals. = 400
inLoop = false ;
inLCounter = 0 ;
};
sphereS.position.x += forInc;
//sphereS.position.x += 0.02403847; // commentary above
if ( sphereS.position.x > 8*r ){
sphereS.position.set( -2*r, -r-q-w, 0 );
};
renderer.render( scene, camera );
}
Hi Vexman. Good to hear from you. Every year or so I keep coming back to PI=4, each time I’ve read Miles’ papers again and think I know the subject, needless to say, I still have plenty to learn.
I corrected a big error in my current angle calculation I’m sure you noticed. I made another ‘correction’, my initial choice of 0.006 as an incremental angle was arbitrary and poor. The total number of increments was between 333 and 334 which made no sense, This time I tried dividing the circle – 2PI rads by 400 (= 0.0157rad) and straight distance 8, by 400 (0.02) .
But that didn’t work. Believe it or not, the PI=4 layout is a lot like an old oscilloscope output display problem. I can synchronize two moving blips along the two tracks by controlling the values of two controls: angle increment and forward increment. Actually I keep var angInc constant and vary var forInc until I arrive at simultaneous tracks, I then look at the values.
var angInc = 0.015707963267949; // 2 PI rad/400
var forInc = 0.0200675; // 0.02 is too slow.
I wish I could explain why I deviate so far from 0.02. I very much enjoy working on such efforts and feel that the only way I can contribute is through dedication and perseverance.
For the time being Nevyn, I can only imagine rolling on the straight track.
.
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
 Re: Animate the PI = 4 experiment
Re: Animate the PI = 4 experiment
Thanks, Vexman, calling it length instead of distance is a bit clearer. I was struggling to get the right words down and even started to get myself confused on exactly where we should be using PI=4 in this setup. In a loose kind of way, I've been assuming that PI=4 is about energy, where-as PI=3.14 is about length.
Airman, one thing to realise about the roll of the ball is that it rolls around the bottom/outer line and not the center line. So make sure that you are using the right radius to calculate that circumference. I haven't checked that, just thought I'd mention it in case. If that is part of the problem, then don't add that outside track to the data, just calculate the difference between the center track and the outside track by using the radius of the ball.
Another thing to mention is that the way you are creating the current code is leading to an animation rather than a simulation. But don't worry about that right now. We will just create another Controller to implement this with physics rather than animation. That's one of the great things about using the MVC architecture.
Airman, one thing to realise about the roll of the ball is that it rolls around the bottom/outer line and not the center line. So make sure that you are using the right radius to calculate that circumference. I haven't checked that, just thought I'd mention it in case. If that is part of the problem, then don't add that outside track to the data, just calculate the difference between the center track and the outside track by using the radius of the ball.
Another thing to mention is that the way you are creating the current code is leading to an animation rather than a simulation. But don't worry about that right now. We will just create another Controller to implement this with physics rather than animation. That's one of the great things about using the MVC architecture.
 Re: Animate the PI = 4 experiment
Re: Animate the PI = 4 experiment
The rolling of the ball should not be a big problem. It should be quite static. You should be able to just give it a rotation and let it go. If the velocity is constant, ignoring curvature, then the roll should be constant too. They are inextricably linked.
 Re: Animate the PI = 4 experiment
Re: Animate the PI = 4 experiment
For the record, I made an error in approximation of ratio in my previous post when looking at motion vs static picture. The correct ratio is Pi(static) / 4= 0,78539816339744830961566084581988 -> it is 21,460183660255169038433915418012 % difference
Airman : "var angInc = 0.015707963267949; // 2 PI rad/400
var forInc = 0.0200675; // 0.02 is too slow. "
The ratio between Pi (static) and Pi (kinetic) should always be constant; 0,78539816339744830961566084581988. in your case I calculated 0,7827563606801545 as the ratio, which is slightly below the actual value. But the focus should be at another issue, in my opinion.
Airman: "This time I tried dividing the circle – 2PI rads by 400 (= 0.0157rad) and straight distance 8, by 400 (0.02) . But that didn’t work."
I think the issue is about the wrong aspect you were looking at. You took static circle's circumference = length and divided it by 400, while looking at the ball in motion. Here it should be PIk applied. In my opinion, the angle increment is 2*Pik / 400 = 0,02 rad within the circle.
Applying the same approach for the straight path, we are looking at 314,15926535897932384626433832795 incremental steps. Expressed in rad, It should be calculated as 2*PIs/314,159265... = 0,02.
In essence, incremental steps expressed in rad should be identical in both cases summing up to 360°. By the end of the event, the ball going through the curved path traveled cca 21,5 % more length in the same amount of time.
Airman : "var angInc = 0.015707963267949; // 2 PI rad/400
var forInc = 0.0200675; // 0.02 is too slow. "
The ratio between Pi (static) and Pi (kinetic) should always be constant; 0,78539816339744830961566084581988. in your case I calculated 0,7827563606801545 as the ratio, which is slightly below the actual value. But the focus should be at another issue, in my opinion.
Airman: "This time I tried dividing the circle – 2PI rads by 400 (= 0.0157rad) and straight distance 8, by 400 (0.02) . But that didn’t work."
I think the issue is about the wrong aspect you were looking at. You took static circle's circumference = length and divided it by 400, while looking at the ball in motion. Here it should be PIk applied. In my opinion, the angle increment is 2*Pik / 400 = 0,02 rad within the circle.
Applying the same approach for the straight path, we are looking at 314,15926535897932384626433832795 incremental steps. Expressed in rad, It should be calculated as 2*PIs/314,159265... = 0,02.
In essence, incremental steps expressed in rad should be identical in both cases summing up to 360°. By the end of the event, the ball going through the curved path traveled cca 21,5 % more length in the same amount of time.
Vexman- Posts : 73
Join date : 2019-02-25
 Re: Animate the PI = 4 experiment
Re: Animate the PI = 4 experiment
.
var angInc = 0.015707963267949; // 2*PI rad/400
var forInc = 0.02008032128500; // 0.02 is too slow.
Absolutely, I agree, the forward increment should be 0.02. I’ve made a coding error somewhere that causes the 0.0000675 difference. I’m not suggesting otherwise.
So in addition to the latest forInc I changed 3 equality checks from strictly greater than (>) to greater than or equal (>=).
if ( (sphereC.position.x > 0) …
to
if ( (sphereC.position.x >= 0) …
No effect.

Showing centers of balls on the centerlines of the tracks.
sphereC.position.set( -2*r, -r, 0 );
sphereS.position.set( -2*r, -r-q-w, 0 );
Both spheres advance thru their straightaways strictly along +x - the forward straight increment
sphereC.position.x += forInc;
sphereS.position.x += forInc;
Once in the loop, sphereC advances around the circular track according to its current angle at radius r.
currentAngle += angInc;
sphereC.position.y = -r*Math.cos(currentAngle);
sphereC.position.x = r*Math.sin(currentAngle);
I don't believe an outside radius nor poor choice of PI is my problem. I believe you identified it when you indicated the need for proper boundary transition detection and response - like proper collision handling. In my case, I’m guessing the ball must initially overshoot the initial circular track section beginning at 6 o’clock. Other than taking the time to chase the problem further - I'll go ahead and try to properly identify the circular track boundary’s exact position. Beginning with determining whether the ball is within a forInc distance from the straight/circular boundary at (0,-r,0).
.
Airman. Here're the latest angleIncrement and forwarIncrement values.Vexman wrote. The ratio between Pi (static) and Pi (kinetic) should always be constant.
var angInc = 0.015707963267949; // 2*PI rad/400
var forInc = 0.02008032128500; // 0.02 is too slow.
Absolutely, I agree, the forward increment should be 0.02. I’ve made a coding error somewhere that causes the 0.0000675 difference. I’m not suggesting otherwise.
So in addition to the latest forInc I changed 3 equality checks from strictly greater than (>) to greater than or equal (>=).
if ( (sphereC.position.x > 0) …
to
if ( (sphereC.position.x >= 0) …
No effect.

Showing centers of balls on the centerlines of the tracks.
Airman. I believe the animate function only uses the track centerlines. The balls’ centers are always advanced or re-positioned onto the track centerlines. Here are the initial set commands:Nevyn wrote. Airman, one thing to realise about the roll of the ball is that it rolls around the bottom/outer line and not the center line. So make sure that you are using the right radius to calculate that circumference. I haven't checked that, just thought I'd mention it in case. If that is part of the problem, then don't add that outside track to the data, just calculate the difference between the center track and the outside track by using the radius of the ball.
sphereC.position.set( -2*r, -r, 0 );
sphereS.position.set( -2*r, -r-q-w, 0 );
Both spheres advance thru their straightaways strictly along +x - the forward straight increment
sphereC.position.x += forInc;
sphereS.position.x += forInc;
Once in the loop, sphereC advances around the circular track according to its current angle at radius r.
currentAngle += angInc;
sphereC.position.y = -r*Math.cos(currentAngle);
sphereC.position.x = r*Math.sin(currentAngle);
I don't believe an outside radius nor poor choice of PI is my problem. I believe you identified it when you indicated the need for proper boundary transition detection and response - like proper collision handling. In my case, I’m guessing the ball must initially overshoot the initial circular track section beginning at 6 o’clock. Other than taking the time to chase the problem further - I'll go ahead and try to properly identify the circular track boundary’s exact position. Beginning with determining whether the ball is within a forInc distance from the straight/circular boundary at (0,-r,0).
Airman. Yes. You succinctly described it before I could put it into words. I’m doing what StevenO did in his PI = 4 experiment, marking the equal velocity/distance sections of the circular track and straight tracks – showing both balls crossing their corresponding marks at the same time. The only difference is, in my math I’m subdividing the tracks into 400 sections instead of 4. In doing so I avoid using PI(g) or PI(k). If I’m mistaken please show me where the animate function uses PI. Calculating sphereC’s track positions with sin and cos and currentAngle is a lot simpler than working with forward vectors and distance calculations, although I would enjoy them more. Solving the problem in this manner – both balls crossing their 400 corresponding track markers at the same time in no way diminishes the kinematics of it.Vexman wrote. In essence, incremental steps expressed in rad should be identical in both cases summing up to 360°.
.
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
 Re: Animate the PI = 4 experiment
Re: Animate the PI = 4 experiment
Airman wrote:I’m subdividing the tracks into 400 sections instead of 4. In doing so I avoid using PI(g) or PI(k). If I’m mistaken please show me where the animate function uses PI.
I'm not familiar with program coding, but as much as I could understand from the code you wrote:
currentAngle += angInc
sphereC.position.y = -r*Math.cos(currentAngle);
sphereC.position.x = r*Math.sin(currentAngle);
...where:
var angInc = velocity * 0.015707963267949; // PI rad/200
var forInc = 0.02008032128500; // 0.02 is too slow.
The way I understand it, you have var angInc set as "velocity * (fixed value of) 0,0157...rad "; the fixed value was calculated by using PI rad / 200. This is where PI(g) was used to set the fix value. When you're calculating SphereC's position using sin or cos and currentAngle, you're indirectly calculating its position using PI(g).
Airman wrote:Both spheres advance thru their straightaways strictly along +x - the forward straight increment
sphereC.position.x += forInc;
sphereS.position.x += forInc;
In my opinion, the straight path should have the increment of 2PI(g)/400 = 0,015707963267949. When you parse the straight track by 400 incremental steps, the ball on the straight path would travel over 2Pi(g)r length, which is what we can observe.
Airman wrote:Once in the loop, sphereC advances around the circular track according to its current angle at radius r.
currentAngle += angInc;
sphereC.position.y = -r*Math.cos(currentAngle);
sphereC.position.x = r*Math.sin(currentAngle);
You're calculating y-axis position of SphereC by using PI(g) for radial increment and this is where I think you should be using PI(k) instead. That would set increment at 0,02 rad. In same delta t, the ball going through the curved path travels over 8r length and the ball going over the straight path travels 2Pi(g)r -> ratio Pi(g)/PI(k) is satisfied -> and that corresponds to ratio forInc / angInc . If the code follows such math, I think it should work.
Vexman- Posts : 73
Join date : 2019-02-25
 Re: Animate the PI = 4 experiment
Re: Animate the PI = 4 experiment
Airman, I forgot to mention, I don't think you've made a coding error that causes the difference. When calculating forInc, I think you should try not to round the fixed value at 15th decimal, which then changes the Pig/PIk ratio. I'd suggest you should try and use 100th decimal (or even bigger). It would help maintain the ratio more-or-less constant, considering there are 400 calculations during a single track run.
Vexman- Posts : 73
Join date : 2019-02-25
 Re: Animate the PI = 4 experiment
Re: Animate the PI = 4 experiment
You can't use 100 decimal places using standard numerical representations in programming languages. There are ways to use an arbitrary number of decimal places, but they would not be used in this type of situation (for efficiency concerns).
If this problem is related to the change from straight section to curved section, then you need to setup the animation so that the transition point is always on a frame change. Alternatively, you have to determine where the change is and calculate both the straight section and the curve for that particular frame (doing the same when it exits the curve too). The latter is more resilient and can handle arbitrarily sized sections, while the former requires that the sections be of certain sizes to accommodate the distance moved each frame which may get tricky because the number of divisions may not work for the curve as it does for the straight.
I recommend calculating both sections in the same frame because that is going to be required when this is done using physics rather than animation. Maybe a better way to say that last part is to be using dynamic calculations rather than pre-calculated data. In essence, they both use physics, but dynamic calculations only take the current position and velocities into account to calculate the changes to the next frame. Where-as an animation just breaks it down into small sections and treats them individually. The difference is kind of like 'the ball is moving' as opposed to 'the ball is being moved'. They may end up looking the same, but dynamic calculations are so much more robust.
For example, the Particle Interaction Model uses dynamic calculations which allows it to handle any situation. We can place protons and neutrons in any configuration and the system still works. Imagine trying to pre-calculate all of those scenarios. A nightmare.
I didn't want to stop your progress, as it is still beneficial to work it out as you are. Once you have a good understanding of the problem, it should make it easier to see how to make it dynamic.
If this problem is related to the change from straight section to curved section, then you need to setup the animation so that the transition point is always on a frame change. Alternatively, you have to determine where the change is and calculate both the straight section and the curve for that particular frame (doing the same when it exits the curve too). The latter is more resilient and can handle arbitrarily sized sections, while the former requires that the sections be of certain sizes to accommodate the distance moved each frame which may get tricky because the number of divisions may not work for the curve as it does for the straight.
I recommend calculating both sections in the same frame because that is going to be required when this is done using physics rather than animation. Maybe a better way to say that last part is to be using dynamic calculations rather than pre-calculated data. In essence, they both use physics, but dynamic calculations only take the current position and velocities into account to calculate the changes to the next frame. Where-as an animation just breaks it down into small sections and treats them individually. The difference is kind of like 'the ball is moving' as opposed to 'the ball is being moved'. They may end up looking the same, but dynamic calculations are so much more robust.
For example, the Particle Interaction Model uses dynamic calculations which allows it to handle any situation. We can place protons and neutrons in any configuration and the system still works. Imagine trying to pre-calculate all of those scenarios. A nightmare.
I didn't want to stop your progress, as it is still beneficial to work it out as you are. Once you have a good understanding of the problem, it should make it easier to see how to make it dynamic.
 Re: Animate the PI = 4 experiment
Re: Animate the PI = 4 experiment
.
Vexman, defining; var angInc = 2*Math.PI/400; // Worked perfectly!
Nevyn, please note I also went ahead and included a circle track boundary detector loop to calculate and include the overShoot just before it happens. I think that does the same as key framing but I haven't really look at your last post.
Status. It appears I can resume forward progress. To be perfectly clear, as our reader can tell, I’m learning as I go along. My console revealed variables at inexplicable counts, and so I had to change them as well but have yet to check.
I still need to ponder your last post, both of you. Thanks for restoring my humility.
.
- Code:
function animate() {
requestAnimationFrame( animate );
var velocity = 1;
var angInc = 2*Math.PI/400;
var forInc = 8/400;
clicks += 1;
if (( sphereC.position.x + forInc >= 0 ) && ( sphereC.position.y = -r ) && ( inLoop = false )) {
overShot = sphereC.position.x + forInc - 0;
var fRatio = overShot/forInc;
currentAngle = -angInc + fRatio*angInc;
};
sphereC.position.x += forInc;
if ((sphereC.position.x >= 0) && ( sphereC.position.y = -r )){
inLoop = true;
};
if ( inLoop ) {
currentAngle += angInc;
sphereC.position.y = -r*Math.cos(currentAngle);
sphereC.position.x = r*Math.sin(currentAngle);
};
if ( (sphereC.position.x >= 0) && ( clicks > 500 )) {
sphereC.position.set( -2*r, -r, 0 );
currentAngle = 0;
inLoop = false ;
clicks = 0 ;
};
sphereS.position.x += forInc;
if ( sphereS.position.x >= 8*r ){
sphereS.position.set( -2*r, -r-q-w, 0 );
};
renderer.render( scene, camera );
}
Vexman, defining; var angInc = 2*Math.PI/400; // Worked perfectly!
Nevyn, please note I also went ahead and included a circle track boundary detector loop to calculate and include the overShoot just before it happens. I think that does the same as key framing but I haven't really look at your last post.
Status. It appears I can resume forward progress. To be perfectly clear, as our reader can tell, I’m learning as I go along. My console revealed variables at inexplicable counts, and so I had to change them as well but have yet to check.
I still need to ponder your last post, both of you. Thanks for restoring my humility.
.
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
 Re: Animate the PI = 4 experiment
Re: Animate the PI = 4 experiment
Nevyn, thank you for correcting me, I learned a new thing.
Airman, I don't want to be pain in the arse, but I think you have forInc and angInc reversed. In my opinion, angInc should be 8/400, and forInc should be 2*Math.Pi/400. Meaning, the ball going through the curve travels 8r and ball over straight path travels 2*Math.Pi*r .
Airman, I don't want to be pain in the arse, but I think you have forInc and angInc reversed. In my opinion, angInc should be 8/400, and forInc should be 2*Math.Pi/400. Meaning, the ball going through the curve travels 8r and ball over straight path travels 2*Math.Pi*r .
Vexman- Posts : 73
Join date : 2019-02-25
 Re: Animate the PI = 4 experiment
Re: Animate the PI = 4 experiment
Something I don't like about that code is that velocity is defined but never used, and time is never mentioned at all. These should be the front-and-center variables, along with distance. Everything should be revolving around them.
I recommend you start another function, maybe call it animateDynamic or something to that effect, that can be used in place of the current animate function. You can swap them as you need while you develop each one. This version will strictly use velocity. Here is the outline of the algorithm:
3) and 4) can actually be combined into the for loop declaration, but it might get tricky, so keep them separate until you can see how that might be done. It basically comes down to while I have time left, give me another section.
4.1) and 4.2) are where you need to handle the difference between a straight and a curve.
I think this algorithm will end up much cleaner
I recommend you start another function, maybe call it animateDynamic or something to that effect, that can be used in place of the current animate function. You can swap them as you need while you develop each one. This version will strictly use velocity. Here is the outline of the algorithm:
- Code:
1) Get current position of ball
2) Calculate next position just using straight line velocity, we only care about length here, not actual position
3) Use current position and next position to determine which track sections we need to handle,
this is why I wanted the length of each section to be in the data
4) For each section, in the order the ball will traverse them:
4.1) Calculate the end position on this section,
the end position is based on the time left for this frame,
or the end of the section, which ever is closer
4.2) Calculate the time it takes to move between the current and end positions
4.3) Move ball to end position
4.4) Subtract time for that change from total time of this frame change (the total time per frame should be a fixed value, not real time)
3) and 4) can actually be combined into the for loop declaration, but it might get tricky, so keep them separate until you can see how that might be done. It basically comes down to while I have time left, give me another section.
4.1) and 4.2) are where you need to handle the difference between a straight and a curve.
I think this algorithm will end up much cleaner
 Re: Animate the PI = 4 experiment
Re: Animate the PI = 4 experiment
.
Good progress today. I made several changes - all that's left are the rolling animations for the ball in the curved track. I look forward to completing this version and moving to the more dynamic code. Correct, I didn't use velocity, I hadn't gotten to it yet, today I did.
1. Verified synchronized tracks. I created a console variable, difClick to verify the two tracks were synchronized – starting and stopping at the same times. The 2 code lines will be left in place but commented out.
2. Track velocity. increments = 400 was just for starters. Since the two tracks are synchronized, increments can now function as an inverse velocity control. Choosing 1000 increments, the two balls take about twenty seconds to complete their tracks. The balls complete 250 increments in about 5 seconds.
3. Moved all the var declarations out of the animate function to the top of the script.

A close up of the circle track's 6 0'clock position.
P.S. Added the animate function and corrected a typo or two. Except for the curved track rolling animation it's close to being rough final complete - well, except for the continuous loop, and a few other things. I'll consider your suggestions and go with your directions.
P.P.S. Make that the whole script. I eliminated a few lines I added while looking at switching forInc and angInc earlier.
.
Good progress today. I made several changes - all that's left are the rolling animations for the ball in the curved track. I look forward to completing this version and moving to the more dynamic code. Correct, I didn't use velocity, I hadn't gotten to it yet, today I did.
1. Verified synchronized tracks. I created a console variable, difClick to verify the two tracks were synchronized – starting and stopping at the same times. The 2 code lines will be left in place but commented out.
2. Track velocity. increments = 400 was just for starters. Since the two tracks are synchronized, increments can now function as an inverse velocity control. Choosing 1000 increments, the two balls take about twenty seconds to complete their tracks. The balls complete 250 increments in about 5 seconds.
3. Moved all the var declarations out of the animate function to the top of the script.
- Code:
<script>
var camera, scene, renderer;
var mesh, sphereC, sphereS;
var r = 1; // Track radius
var cTrackCenter = new THREE.Vector3( 0, 0, 0 ) ;
var q = .2; // track separation
var w = 0.75 * r; // track width
var bRadius = w / 2 ;
var bCircum = 2 * Math.PI * bRadius;
var increments = 250;
// Inverse velocity. The greater the number of increments the slower the ball's velocity along the track.
var forInc = 8/increments;
//var forInc = 2*Math.PI*r/increments;
var angInc = 2*Math.PI*r/increments;
//var angInc = 8/increments;
var ang2rot = 10*r/bCircum; // the number of rolling rotations
var ang2Inc = 2*ang2rot/increments; // the rolling ball is rolling
//var cSphereAxis;
var curTrackAngle = 0;
var curBallAngle = 0;
var inLoop = false;
var overShot, fRatio;
var cClicks = 0;
var sClicks = 0;
init();
animate();
function init() {
camera = new THREE.PerspectiveCamera( 70, window.innerWidth / window.innerHeight, 1, 1000 );
camera.position.set( 3*r, 0, 5*r ); // ( 3*r, -r, 5*r );
scene = new THREE.Scene();
// Set the background color // default black
// scene.background = new THREE.Color('#0000FF'); // #009900 pool table green // #0000FF nice high contrast blue //
var sphereMat = new THREE.MeshBasicMaterial( { wireframe: true, color: 'yellow' } );
var material = new THREE.LineBasicMaterial( { color: 'yellow' } ); // markers
var MAT_LINE_CP = new THREE.LineBasicMaterial( { color: 0x00cc00, linewidth: 0.25 } ); // distances
// 3 concentric curved paths
for(th=1;th<=360;th+=1) {
var radians1 = (Math.PI/180) * th;
var radians2 = (Math.PI/180) * (th + 1);
if (th === 359) { radians2 = (Math.PI/180) }
for ( i = -1; i < 2; i++ ) {
configRadius = r + i*w/2;
var XYPlaneLine = new THREE.Geometry();
XYPlaneLine.vertices.push( //viewing x and y.
new THREE.Vector3( configRadius * Math.cos(radians1) + cTrackCenter.x, configRadius*Math.sin(radians1) + cTrackCenter.y, 0 ),
new THREE.Vector3( configRadius * Math.cos(radians2) + cTrackCenter.x, configRadius*Math.sin(radians2) + cTrackCenter.y, 0 ));
var XYLine = new THREE.Line( XYPlaneLine, MAT_LINE_CP);
scene.add(XYLine);
};
};
// S track markers
var geometry = new THREE.Geometry( 1, 1, 1 );
geometry.vertices.push(new THREE.Vector3( 2*r*Math.PI, -r-q-w/2, 0 ) );
geometry.vertices.push(new THREE.Vector3( 2*r*Math.PI, -r-q-1.5*w, 0 ) );
var line = new THREE.Line( geometry, material );
scene.add( line ); // PI marker
for ( j = 0; j < 6; j++ ) {
var geometry = new THREE.Geometry( 1, 1, 1 );
geometry.vertices.push(new THREE.Vector3( -2*r+2*r*j, -r-q-w/2, 0 ) );
geometry.vertices.push(new THREE.Vector3( -2*r+2*r*j, -r-q-1.5*w, 0 ) );
var line = new THREE.Line( geometry, material );
scene.add( line ); // Section markers
}
// C track straight section markers
for ( m = 0; m < 2; m++ ) {
var geometry = new THREE.Geometry( 1, 1, 1 );
geometry.vertices.push(new THREE.Vector3( -2*r+2*r*m, -r+w/2, 0 ) );
geometry.vertices.push(new THREE.Vector3( -2*r+2*r*m, -r-w/2, 0 ) );
var line = new THREE.Line( geometry, material );
scene.add( line );
}
for ( k = -1; k < 2; k++ ) {
// S track lengths: top edge, centerline and bottom edge
var geometry = new THREE.Geometry( 1, 1, 1 );
geometry.vertices.push(new THREE.Vector3( -2*r, -r-w-q+k*w/2, 0 ) );
geometry.vertices.push(new THREE.Vector3( 8*r, -r-w-q+k*w/2, 0 ) );
var line = new THREE.Line( geometry, MAT_LINE_CP );
scene.add( line );
// C track lengths: top edge, centerline and bottom edge
var geometry = new THREE.Geometry( 1, 1, 1 );
geometry.vertices.push(new THREE.Vector3( -2*r, -r+k*w/2, 0 ) );
geometry.vertices.push(new THREE.Vector3( 0, -r+k*w/2, 0 ) );
var line = new THREE.Line( geometry, MAT_LINE_CP );
scene.add( line );
}
// C track markers
var geometry = new THREE.Geometry( 1, 1, 1 );
geometry.vertices.push(new THREE.Vector3( r-w/2, 0, 0 ) );
geometry.vertices.push(new THREE.Vector3( r+w/2, 0, 0 ) );
var line = new THREE.Line( geometry, material );
scene.add( line ); // C track One Marker
var geometry = new THREE.Geometry( 1, 1, 1 );
geometry.vertices.push(new THREE.Vector3( 0, r+w/2, 0 ) );
geometry.vertices.push(new THREE.Vector3( 0, r-w/2, 0 ) );
var line = new THREE.Line( geometry, material );
scene.add( line ); // C track Two Marker
var geometry = new THREE.Geometry( 1, 1, 1 );
geometry.vertices.push(new THREE.Vector3( -r-w/2, 0, 0 ) );
geometry.vertices.push(new THREE.Vector3( -r+w/2, 0, 0 ) );
var line = new THREE.Line( geometry, material );
scene.add( line ); // C track Three Marker
// Balls
var sphereGeom = new THREE.SphereGeometry( bRadius, 8, 8 );
sphereC = new THREE.Mesh( sphereGeom, sphereMat );
sphereC.position.set( -2*r, -r, 0 );
sphereS = new THREE.Mesh( sphereGeom, sphereMat );
sphereS.position.set( -2*r, -r-q-w, 0 );
var ballOne = new THREE.Object3D();
ballOne.add(sphereC);
var ballTwo = new THREE.Object3D();
ballTwo.add(sphereS);
scene.add( ballOne, ballTwo );
// scene.rotation.x += -Math.PI/6;
scene.rotation.x += -Math.PI/6;
renderer = new THREE.WebGLRenderer();
renderer.setPixelRatio( window.devicePixelRatio );
renderer.setSize( window.innerWidth, window.innerHeight );
document.body.appendChild( renderer.domElement );
window.addEventListener( 'resize', onWindowResize, false );
}
function onWindowResize() {
camera.aspect = window.innerWidth / window.innerHeight;
camera.updateProjectionMatrix();
renderer.setSize( window.innerWidth, window.innerHeight );
}
function animate() {
requestAnimationFrame( animate );
cClicks += 1;
sClicks += 1;
if (( sphereC.position.x + forInc >= 0 ) && ( sphereC.position.y = -r ) && ( inLoop = false )) {
overShot = sphereC.position.x + forInc - 0;
fRatio = overShot/forInc;
curTrackAngle = -angInc + fRatio*angInc;
};
sphereC.rotation.y += ang2Inc;
sphereC.position.x += forInc;
if ((sphereC.position.x >= 0) && ( sphereC.position.y = -r )){
inLoop = true;
};
if ( inLoop ) {
curTrackAngle += angInc;
sphereC.position.y = -r*Math.cos(curTrackAngle);
sphereC.position.x = r*Math.sin(curTrackAngle);
};
if ( (sphereC.position.x >= 0) && ( cClicks > increments*1.25 )) {
sphereC.position.set( -2*r, -r, 0 );
curTrackAngle = 0;
inLoop = false ;
cClicks = 0 ;
};
sphereS.rotation.y += ang2Inc;
sphereS.position.x += forInc;
if (( sphereS.position.x >= 8*r ) && ( sClicks > increments*1.25 )){
sphereS.position.set( -2*r, -r-q-w, 0 );
curBallAngle = 0;
sClicks = 0;
};
//var difClick = cClicks - sClicks; // consistently zero.
//console.log( 'difClick = ' + difClick );
renderer.render( scene, camera );
}
</script>

A close up of the circle track's 6 0'clock position.
Airman. No problem, except I don’t exactly see what you’re saying. My success using the increment variable as an inverse velocity would seem to me to strongly suggest there’s no problem with the code. I tried switching the two variables, which increased the speed through the curve but slowed the speed through the straight, as would be expected. The above diagram shows a length where both distances overlap, just to the left of the magenta vertical line going through (0, -r, 0 ), confirming the incorrect linear distance comparison, 4PI(g)/400/8/400 = PI(g)/4.Vexman wrote. Airman, I don't want to be pain in the arse, but I think you have forInc and angInc reversed. In my opinion, angInc should be 8/400, and forInc should be 2*Math.Pi/400. Meaning, the ball going through the curve travels 8r and ball over straight path travels 2*Math.Pi*r .
P.S. Added the animate function and corrected a typo or two. Except for the curved track rolling animation it's close to being rough final complete - well, except for the continuous loop, and a few other things. I'll consider your suggestions and go with your directions.
P.P.S. Make that the whole script. I eliminated a few lines I added while looking at switching forInc and angInc earlier.
.
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
 Re: Animate the PI = 4 experiment
Re: Animate the PI = 4 experiment
(scratching my head)....Uhmm...well, I may have misread or misunderstood what you wrote in an earlier version. Thanks for your patience and motivation, though, when dealing with my comments.Airman wrote:Airman. No problem, except I don’t exactly see what you’re saying. My success using the increment variable as an inverse velocity would seem to me to strongly suggest there’s no problem with the code. I tried switching the two variables, which increased the speed through the curve but slowed the speed through the straight, as would be expected. The above diagram shows a length where both distances overlap, just to the left of the magenta vertical line going through (0, -r, 0 ), confirming the incorrect linear distance comparison, 4PI(g)/400/8/400 = PI(g)/4.
With the new code version, I'm completely lost and not versed enough to locate supporting math.
When mentioning speed - the speed through the curve should be increased in comparison to the speed through the straight, as the curve is cca 21,5% longer in distance (same delta t). Speed change / increase within the curve is an expected outcome, no? Meaning, if the two balls were at the same length from the starting point when one ball is crossing the beginning of curved section, by the end of the curve, one ball covered more length in same amount of time. So its velocity had to change in comparison to the other ball. Pi(k) is saying exactly that.
Regarding 4PI(g)/400/8/400 : why is there 4Pi(g) rad / 400 suddenly involved? I can't seem to understand where number 4 came from. 2Pig rad / 400 is the length of the straightened out circumference section. 8 rad / 400 is the length of curved section. PI(g)/4 = 2Pi(g)rad/400/8 rad / 400 is true. I fail to find (and understand) what math supports your claim angInc = 4Pi(g) rad / 400 ...
About the diagram: was it drawn before or after you switched the variables? Because the text in the diagram says forInc=8/400, which is not correct in my opinion. Forward increment is along x-axis only, with 2Pi(g) rad /400 increments. Angular increment is along x- and y-axis, with 8 rad /400 increments.
Vexman- Posts : 73
Join date : 2019-02-25
 Re: Animate the PI = 4 experiment
Re: Animate the PI = 4 experiment
Some of your if statements are failing because you have used the assignment operator (=) instead of the comparison operator (==).
e.g.
The first condition, ( sphereC.position.x + forInc >= 0 ), is fine and works as expected.
The second condition, ( sphereC.position.y = -r ), is actually assigning -r to sphereC.position.y. It is not comparing those values. Once it is assigned, the condition succeeds (evaluates to true) because sphereC.position.y has a value, not because it equals -r (even though it always will because we just assigned that value to it, it is not doing a comparison at all).
The third condition, ( inLoop = false ), does the same thing and sets the value of inLoop to false, which is then evaluated as false, and so the whole if statement fails and execution will never go in there.
Same with this block, except this one fails true, so it will always execute this code if the first condition is satisfied and will ignore the second:
sphereC.position.y = -r assigns -r to sphereC.position.y again. You must use double equals for comparison. Try to think of the comparison as 2 words like 'equal to', instead of just 'equals' which links to the 2 equal signs in the comparison operator, '=='. Think of the first = as 'equal' and the second = as 'to' and it will be easier to remember, or find some other way to remember it that works for you.
e.g.
- Code:
if (( sphereC.position.x + forInc >= 0 ) && ( sphereC.position.y = -r ) && ( inLoop = false )) {
overShot = sphereC.position.x + forInc - 0;
fRatio = overShot/forInc;
curTrackAngle = -angInc + fRatio*angInc;
};
The first condition, ( sphereC.position.x + forInc >= 0 ), is fine and works as expected.
The second condition, ( sphereC.position.y = -r ), is actually assigning -r to sphereC.position.y. It is not comparing those values. Once it is assigned, the condition succeeds (evaluates to true) because sphereC.position.y has a value, not because it equals -r (even though it always will because we just assigned that value to it, it is not doing a comparison at all).
The third condition, ( inLoop = false ), does the same thing and sets the value of inLoop to false, which is then evaluated as false, and so the whole if statement fails and execution will never go in there.
Same with this block, except this one fails true, so it will always execute this code if the first condition is satisfied and will ignore the second:
- Code:
if ((sphereC.position.x >= 0) && ( sphereC.position.y = -r )){
inLoop = true;
};
sphereC.position.y = -r assigns -r to sphereC.position.y again. You must use double equals for comparison. Try to think of the comparison as 2 words like 'equal to', instead of just 'equals' which links to the 2 equal signs in the comparison operator, '=='. Think of the first = as 'equal' and the second = as 'to' and it will be easier to remember, or find some other way to remember it that works for you.
 Re: Animate the PI = 4 experiment
Re: Animate the PI = 4 experiment
.

I've made corrections and am happy with this diagram. It agrees with what I coded and aids in the discussion. I even quoted your 21% measured value observation.
I like working with others and generally don't fault errors. It's all about Teamwork, commitment and getting things done. Thanks for cooperating. I’m always keen to create a new diagram. As usual, I make plenty of mistakes, thanks for pointing them out. Proof that by working as a team I can achieve more with others than I can on my own.
Starting with a circular path with radius r. The length of the straight path must then be 8r. Divide both tracks into 400 increments and view the circular track’s 6 o’clock position as shown.
Do we still have a disagreement? Are there any changes you'd like to suggest?
Thanks for the corrections Nevyn. I didn't make many errors. Sure, I've considered the difference between equal and equal to before, but had no idea that by using equal I was assigning values within the if statements. I do get embarrassed at times. Thanks again for working with me and for your patience.
.

I've made corrections and am happy with this diagram. It agrees with what I coded and aids in the discussion. I even quoted your 21% measured value observation.
I like working with others and generally don't fault errors. It's all about Teamwork, commitment and getting things done. Thanks for cooperating. I’m always keen to create a new diagram. As usual, I make plenty of mistakes, thanks for pointing them out. Proof that by working as a team I can achieve more with others than I can on my own.
Starting with a circular path with radius r. The length of the straight path must then be 8r. Divide both tracks into 400 increments and view the circular track’s 6 o’clock position as shown.
Do we still have a disagreement? Are there any changes you'd like to suggest?
Thanks for the corrections Nevyn. I didn't make many errors. Sure, I've considered the difference between equal and equal to before, but had no idea that by using equal I was assigning values within the if statements. I do get embarrassed at times. Thanks again for working with me and for your patience.
.
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
 Re: Animate the PI = 4 experiment
Re: Animate the PI = 4 experiment
Don't be embarrassed about that. Very easy, and very common, mistake to make. If, as a learning programmer, you don't make that mistake, then you probably aren't writing enough code.
It is important to realise that a statement in a programming language is a self-contained entity. It does not care where it is in the code. It does not get interpreted differently just because it is the condition in an if statement. This sort of stuff becomes more apparent when you write your own language. You start to see the language in its building blocks. I'll see if I can explain it.
At the most basic level, an if statement looks like this:
if statement then statement else statement
So it is really a construct that contains 3 statements (and one of them is optional). However, not all of those statements are treated equally. The first statement is called the condition and is expected to evaluate to a boolean value. Some languages absolutely require that and others will attempt to force it into one. Javascript is the type to force it, which means it will not generate an error unless it can't find a way to make it into a boolean (spoiler, it always can).
Now, you might be a little confused by the fact that the then and else statements are a single statement and not multiple. I'm sure you have written them with multiple statements, but that isn't strictly correct. It might look like multiple statements, but it is actually a single block statement, that then contains multiple statements.
In javascript, a block is encapsulated by { and }, and may contain any number of statements inside of it.
Generally, in Javascript and some other languages, a statement is terminated by a semi-colon, ;. However, some languages don't always require it if they can determine that it is the end of statement without it. I prefer to put them in regardless.
It is important to realise that a statement in a programming language is a self-contained entity. It does not care where it is in the code. It does not get interpreted differently just because it is the condition in an if statement. This sort of stuff becomes more apparent when you write your own language. You start to see the language in its building blocks. I'll see if I can explain it.
At the most basic level, an if statement looks like this:
if statement then statement else statement
So it is really a construct that contains 3 statements (and one of them is optional). However, not all of those statements are treated equally. The first statement is called the condition and is expected to evaluate to a boolean value. Some languages absolutely require that and others will attempt to force it into one. Javascript is the type to force it, which means it will not generate an error unless it can't find a way to make it into a boolean (spoiler, it always can).
Now, you might be a little confused by the fact that the then and else statements are a single statement and not multiple. I'm sure you have written them with multiple statements, but that isn't strictly correct. It might look like multiple statements, but it is actually a single block statement, that then contains multiple statements.
In javascript, a block is encapsulated by { and }, and may contain any number of statements inside of it.
Generally, in Javascript and some other languages, a statement is terminated by a semi-colon, ;. However, some languages don't always require it if they can determine that it is the end of statement without it. I prefer to put them in regardless.
 Re: Animate the PI = 4 experiment
Re: Animate the PI = 4 experiment
OK, I've made a silly error and would like to apologize for the possible confusion it may caused. Hope you won't hold it against me. I've somehow overlooked the way you visualized the whole concept and have made wrong conclusions about a few things. It made me blush when I finally comprehended my mistake.
a) the length of the straight track from the start to the finish line is, of course, 8r . How else could it demonstrate that both straight and curved paths are of equallengths distances? But it didn't occur to me earlier that crossing the finish line means both balls have moved over the same 8r distance.
b) Of course, the section increment of straight track, forInc, is equal to 8/400 rad; angInc is equal to 2Pi(g)/400. My understanding of it was reversed.
c) If straight path = 8r, then I think my statement (which you quoted) is partially correct or plain wrong. The length of curved path is not measured 21,5% longer than the length of straight path; 8r=8r . Much more precise would be to say that the length of curved path is measured 21,5% longer than that, which is descirbed by the length of curve's circumference (2PIr).
a) the length of the straight track from the start to the finish line is, of course, 8r . How else could it demonstrate that both straight and curved paths are of equal
b) Of course, the section increment of straight track, forInc, is equal to 8/400 rad; angInc is equal to 2Pi(g)/400. My understanding of it was reversed.
c) If straight path = 8r, then I think my statement (which you quoted) is partially correct or plain wrong. The length of curved path is not measured 21,5% longer than the length of straight path; 8r=8r . Much more precise would be to say that the length of curved path is measured 21,5% longer than that, which is descirbed by the length of curve's circumference (2PIr).
Last edited by Vexman on Thu Sep 26, 2019 12:22 pm; edited 1 time in total (Reason for editing : strike-through text)
Vexman- Posts : 73
Join date : 2019-02-25
 Re: Animate the PI = 4 experiment
Re: Animate the PI = 4 experiment
.

Thanks Vexman. Here’s the latest iteration - the best yet - close up of the curved track start/finish line. I find this all very satisfying work, Please don’t hesitate to comment, add to or point out any error – etc.
I see Nevyn has replied to your other post - good - I have little to no confidence in answering 'atmospheric atomic charge flow' questions. I'll try to follow if you lead.

PI=4 Experiment. Bottom edge view, the tracks form the center horizontal green line parallel to the x-axis. The image shows two series of images, each about 2.5 seconds apart. increments = 6000 and it takes a minute to reach this position and another minute to complete the tracks.
The straight path sphere is ‘rolling’ along in the x direction - just before, during, and after its spin axis aligns with the camera’s x position at 3*r. The camera is pointed in the positive y direction. The small sphere to the left is the ball moving along the curved track. SphereGeometry( bRadius, 16, 3 ) makes the sphere appear as a rolling – 32 triangular sided cylinder capped with 16 sided cones each one third the total diameter on the spin axis – a very short pencil with two long sharp ends – the closest will point directly at the viewer. Intended to emphasize and allow a close review of the sphere’s rolling rate.
Straight rolling. I reported that I’d coded the animation for the ball rolling along the straight track, but the rotation rate wasn’t correct. I think I corrected it and the fix deserves some discussion.
These are the pertinent variables and their values.
// Inverse velocity. The greater the number of increments the slower the ball's velocity along the track.
The main change is the addition of var kMult = (4/Math.PI); The constant that allows us to account for the increased length of the curve due to curved motion. Note the ball radius, and circumference, bRadius, bCircum. Also ang2rot, the total number of rolling rotations for the total straight track, and ang2Inc is the straight ball’s rolling increment.
To make a long story short, it’s a cycloid. We all know a good roll when we see it. I tried dividing the total length of the straight path by the ball’s geometric circumference and could not achieve a realistic roll - the top row of images. The tangent where the surface should reach zero velocity contact would instead glide forward over the track's imagined surface. When I introduced the kinematic multiplier, kMult = 4/PI(g), I saw proper rolling; the bottom row of three images.
Another example. Stuff like this is part of the reward of making this project effort in the first place. I suppose It would take program modifications (hint, hint) to study it further.
.

Thanks Vexman. Here’s the latest iteration - the best yet - close up of the curved track start/finish line. I find this all very satisfying work, Please don’t hesitate to comment, add to or point out any error – etc.
I see Nevyn has replied to your other post - good - I have little to no confidence in answering 'atmospheric atomic charge flow' questions. I'll try to follow if you lead.

PI=4 Experiment. Bottom edge view, the tracks form the center horizontal green line parallel to the x-axis. The image shows two series of images, each about 2.5 seconds apart. increments = 6000 and it takes a minute to reach this position and another minute to complete the tracks.
The straight path sphere is ‘rolling’ along in the x direction - just before, during, and after its spin axis aligns with the camera’s x position at 3*r. The camera is pointed in the positive y direction. The small sphere to the left is the ball moving along the curved track. SphereGeometry( bRadius, 16, 3 ) makes the sphere appear as a rolling – 32 triangular sided cylinder capped with 16 sided cones each one third the total diameter on the spin axis – a very short pencil with two long sharp ends – the closest will point directly at the viewer. Intended to emphasize and allow a close review of the sphere’s rolling rate.
Straight rolling. I reported that I’d coded the animation for the ball rolling along the straight track, but the rotation rate wasn’t correct. I think I corrected it and the fix deserves some discussion.
These are the pertinent variables and their values.
// Inverse velocity. The greater the number of increments the slower the ball's velocity along the track.
- Code:
// Inverse velocity. The greater the number of increments the slower the ball's velocity along the track.
var increments = 6000; // Just over two minutes to complete the courses.
var forInc = 8/increments;
var angInc = 2*Math.PI*r/increments;
var kMult = (4/Math.PI);
//var kMult = 1;
var bRadius = w;
var bCircum = 2 * Math.PI * bRadius; // * kMult;
var ang2rot = 10*r/bCircum; // 8*r*kMult/bCircum; //the number of rolling rotations for the total
var ang2Inc = 4 * ang2rot * kMult/ increments; // the straight ball is rolling
The main change is the addition of var kMult = (4/Math.PI); The constant that allows us to account for the increased length of the curve due to curved motion. Note the ball radius, and circumference, bRadius, bCircum. Also ang2rot, the total number of rolling rotations for the total straight track, and ang2Inc is the straight ball’s rolling increment.
To make a long story short, it’s a cycloid. We all know a good roll when we see it. I tried dividing the total length of the straight path by the ball’s geometric circumference and could not achieve a realistic roll - the top row of images. The tangent where the surface should reach zero velocity contact would instead glide forward over the track's imagined surface. When I introduced the kinematic multiplier, kMult = 4/PI(g), I saw proper rolling; the bottom row of three images.
Another example. Stuff like this is part of the reward of making this project effort in the first place. I suppose It would take program modifications (hint, hint) to study it further.
.
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
 Re: Animate the PI = 4 experiment
Re: Animate the PI = 4 experiment
.

The balls are centered their own radii above the track. increments = n = 1000. Each track is divided into n incremental markers – grey lines orthogonal to the rolling direction, making it easy to confirm good rolling action when treating the ball’s straight rolling distance as a cycloid.
I'm considering changing those orthogonal lines into orthogonal circles which the ball will pass through - giving a tube-like appearance. I'll see how it looks and share it if it works.
Made the following changes to the tracks:
In the init function. I added straight and curved track increment markers – code below. I also cleaned up the comments, line and curve section titles.

The balls are centered their own radii above the track. increments = n = 1000. Each track is divided into n incremental markers – grey lines orthogonal to the rolling direction, making it easy to confirm good rolling action when treating the ball’s straight rolling distance as a cycloid.
I'm considering changing those orthogonal lines into orthogonal circles which the ball will pass through - giving a tube-like appearance. I'll see how it looks and share it if it works.
Made the following changes to the tracks:
In the init function. I added straight and curved track increment markers – code below. I also cleaned up the comments, line and curve section titles.
- Code:
// S track Increment markers increments
for ( n = 0; n < increments; n++ ) {
var geometry = new THREE.Geometry( 1, 1, 1 );
geometry.vertices.push(new THREE.Vector3( -2*r+n*10/increments, -r-q-w/2, 0 ) );
geometry.vertices.push(new THREE.Vector3( -2*r+n*10/increments, -r-q-1.5*w, 0 ) );
var line = new THREE.Line( geometry, material2 );
scene.add( line );
};
// C track Increment markers
for( ang=0; ang<=increments; ang+=1 ) {
var cDist = 2*Math.PI/increments * ang;
var geometry = new THREE.Geometry( 1, 1, 1 );
geometry.vertices.push(new THREE.Vector3(iRadius*Math.cos(cDist)+cTrackCenter.x, iRadius*Math.sin(cDist)+ cTrackCenter.y, 0));
geometry.vertices.push(new THREE.Vector3(oRadius*Math.cos(cDist)+cTrackCenter.x, oRadius*Math.sin(cDist)+ cTrackCenter.y, 0));
var line = new THREE.Line(geometry, material2 );
scene.add( line );
};
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
 Re: Animate the PI = 4 experiment
Re: Animate the PI = 4 experiment
.
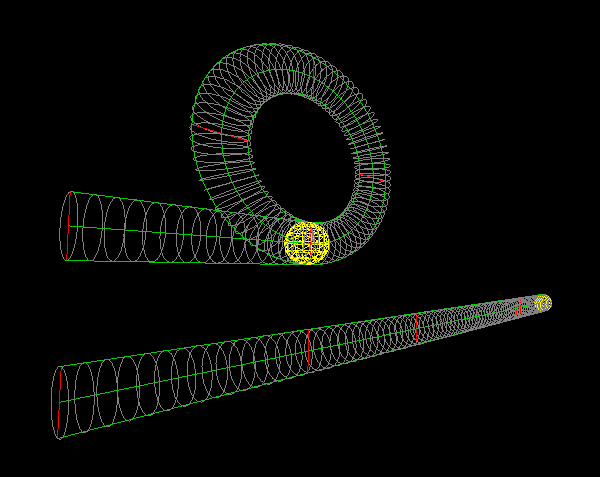
Tubular tracks. Each track shows 100 circles or hoops the balls must travel through. Please excuse the field of view distortion.
I must admit, they look better than I expected. I don't know if you wanted tube geometry or not. Flaming hoops might make a decent animation. Working out the details of arranging the hoops about the circular track provided some clues that might prove helpful in solving that last curved ball’s animation.
.

Tubular tracks. Each track shows 100 circles or hoops the balls must travel through. Please excuse the field of view distortion.
I must admit, they look better than I expected. I don't know if you wanted tube geometry or not. Flaming hoops might make a decent animation. Working out the details of arranging the hoops about the circular track provided some clues that might prove helpful in solving that last curved ball’s animation.
.
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
 Re: Animate the PI = 4 experiment
Re: Animate the PI = 4 experiment
This really looks impressive, Airman.
Will you consider making such animation accessible at some website, open for general public? It would make an excellent accessory when discussing Pi(k) with people having different opinion about what's going on inside the curve when motion is involved.
Will you consider making such animation accessible at some website, open for general public? It would make an excellent accessory when discussing Pi(k) with people having different opinion about what's going on inside the curve when motion is involved.
Vexman- Posts : 73
Join date : 2019-02-25
Page 1 of 8 • 1, 2, 3, 4, 5, 6, 7, 8 
 Similar topics
Similar topics» PI NINE - Pi experiment with two edge track
» How about an Experiment to Simulate Attraction?
» The Event Horizon Telescope experiment
» Photonics experiment resolves quantum paradox
» Revisiting the Pound-Rebka experiment in light of Miles' new Gravity Paper and the Charge Field
» How about an Experiment to Simulate Attraction?
» The Event Horizon Telescope experiment
» Photonics experiment resolves quantum paradox
» Revisiting the Pound-Rebka experiment in light of Miles' new Gravity Paper and the Charge Field
Page 1 of 8
Permissions in this forum:
You cannot reply to topics in this forum