Animate the PI = 4 experiment

I think this might be overkill. Too much information hides the stuff you really want to get to. I had a quick go at making lots of markers with short distances between them, but it just becomes a mess. They won't line up with what you want anyway. You could calculate it to do what you want, but then it isn't really testing anything because it would be using the same assumptions on both sides. You'll just have to rely on the math.

I don't think showing the cycloid nature is something that this app needs to do. Besides, a PI=3.14 curve will still show the same motion, but with a smaller distance between points.

Creating a line to represent the cycloid is easy enough. I'll have a go at that when I get the chance. I should be able to add it to a Ball through the modifier property, so nothing else needs to change.

So the cycloids turned out better than I thought.



A bit of a shame they are visible from the side.

thank you for this work. I look forward to trying to read it all and even to understand it.

The physics of the StevenO [or is it SteveO] is a favorite. trying to debunk it was not possible for me. It appears to prove something. What or how it proves it I  cannot yet say. the problem proposed by MM is involved and I cannot decide what I can say about his work either. love it!

I am a builder, and I dream of setting up the same experiment. I want to try to set up other physical experiments, this I would do to penetrate deeper into what is happening, and how best to describe what is happening mathematically. The goal would be contributing something towards what has already been done.

The original discussion in "recent papers" I read carefully. but cannot comment.

I am an outsider to programming, i will try not to clutter up your conversation further!


thanks again

.

Perfect Nevyn, the cycloids work much better than track markers. Being separate from the markers, yet identifying the same locations makes cycloids a fine addition/alternative.

//////\\\\\\//////\\\\\\//////\\\\\\

Welcome 3rd doorman, thanks for the positive feedback, I’m glad Nevyn gets to hear it from someone beside me for once.

StevenO is, of course, Steven Oostdijk; no disrespect intended, I started calling him StevenO because of a dread fear of mis-spelling his name. I think Nevyn may have refereed to him as SteveO. If you like, as a registered member you may try sending a message to soostdijk himself.

Feel free to question, comment, contribute or ask for help. Like anything else, it gets easier with practice. If your comment doesn’t seem to fit any topic, start a new one. If you’re trying to further your understanding of Miles’ work, forcing yourself to communicate with others on the subject definitely helps, not to mention the feedback you receive.
.

I've done a massive code restructure. The JS file with all of the classes was getting too large to work in effectively. So I've pulled out each area into its own file. I haven't merged it onto the master branch yet, so have a look at the source-code-restructure branch to see what I have done. When you are happy with it, I'll merge it in.

.

Thanks for the warning, I noticed you made many changes today, including the few most recent "massive ones" at the top. I’m ready.
.

Ok, that's merged in now.

Everything looks good to me.

.

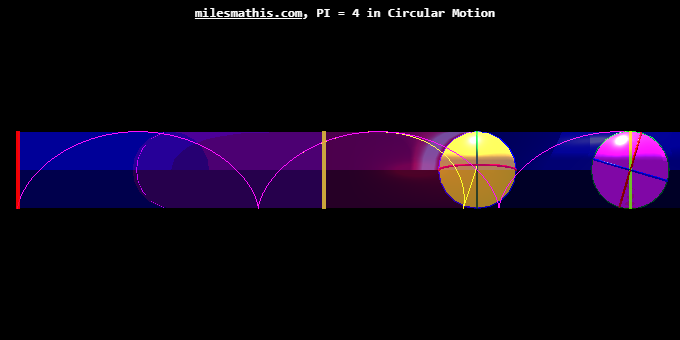
Debuting a new geometric pi, piG straight track. Like the piG curved track, the piG straight track demonstrates the mainstream expected, physics violating motion based on the assumption that the distances traveled by the balls are equal to the geometric pi lengths. The false notional piG tracks (green and LtBlue balls) are compared and contrasted with the actual results demonstrated by the PI = 4 experiment (yellow and magenta balls) which show that given curved motion, kinematic pi, piK = 4. Above, the piG balls have completed their runs at 2*radius + 2*(3.14..), the piK balls will soon complete their runs at 2*radius + 8*radius.


Here’s the same distances traveled from a different angle and including the balls’ cycloids.

Your changes have transformed the code faster than I can follow. There’s one item left on our functional wish list - advance by a single frame. This may be done by repeated spacebar presses or some other unique keyboard character, not including the arrow key which is used by the orbital camera.
.

Done, with a few more goodies for you.

But I wouldn't be so quick to judge the PI=4 as a absolute winner. Look closely at the straight kinematic track without markers showing and you will see that the bounce points (of the cycloid tracker) is smoothed out on the bottom. This is not good, although we don't expect PI=4 to work for straight sections since they are not curved. The cycloid tracker on the kinematic curve itself looks fine.

I still don't like the way the kinematic curve track slows down for the curve and speeds back up for the straight. The geometric curve gives a smoother motion around the full track.

As far as rolling goes, neither of them look right on a straight. It seems to me, just eye-balling it, that the ideal roll is somewhere between 3.14 and 4. How does that work? I don't know, just saying as I see it.

.

A side view showing the green piG and magenta piK straight balls. The green ball is stopped while the magenta continues to roll forward, toward the right. The image includes the cycloids previously traced by the green ball’s red marker at just past 9 o’clock, and the magenta red marker at just after 10 o’clock. The straight track’s 6*radius and 2*(3.14…)*radius markers are barely visible. The tight v of the green cycloid agrees with the expected cycloid curve shape. The magenta cycloid’s surface contact point is spread out in what appears to be a curtate cycloid, the line that would be expected to be traced out by a point just inside the piK ball’s surface contact point, slightly closer to the ball's center. We know that both ball radii are the same, the slightly ‘higher’ appearing magenta line is due to a slightly different angle. If the point creating the curve were slightly outside the ball’s surface the resulting cycloid would include loops and be called a prolate cycloid. Does the spread out curtate cycloid form here indicate a little bit of piK forward gliding?  

Thank you Sir, goodies galore, including a half dozen or so new key command options, such as the speed up and slow down velocity + - keys. Indicating each new keyboard equivalent on the datGUI panel is a nice touch.

Maybe we can include 4 toggle switches corresponding to the 4 track array to allow someone to omit tracks, as I did with these two images, in order to better compare just straight to straight or curved to curved.

I noticed the cycloids. After fervently requesting a means whereby anyone may confirm, to their complete and utter satisfaction, good ball rolling, how could I expect that we might be unsatisfied? On the other hand, I’m not at all disappointed. The joy of effort and discovery should include surprises.
 
Here’s a top view of the curved piG and piK tracks. Why the cusps? I would expect the cycloid curve would always remain aligned with the curved track center-line.

.

My understanding is that the piK rolling on a straight section is rolling too slowly, so it drags out the cusp and it loses its point. In the curve, however, it regains that point, indicating that the curve brings it all into line so that things work correctly. It may be that the ball should be using piG rolling in straight sections, and piK rolling in curved sections on any kinematic track.

I'll see what I can do about changing tracks. It will shake things up a bit.

The point of the cusp will align with the center-line of the track, and so will the top of the cycloid curve. However, all other points will be off that center-line. The only part of the ball that is always on the center-line is the center of the ball. We are measuring a point on the surface, so it only coincides with the center at the top and bottom of its rotation. At all other times it is along the tangent from the center of the ball.

.

This composite image is intended to show the piK curved track’s yellow cycloid from 2 different directions. At the bottom, the ball’s initial straight section is at the left where the ball approached the viewer before turning onto the curved track toward the right. The ball is shown halfway through the the circular track’s final quarter in order to better display the cycloid transition from the straight to the circular track.

Unable to omit all but the piK track without error (and resulting in a prettier picture if you ask me), the upper image superimposes both piK and piG circular tracks. Both balls are in their end positions, the ltBlue piG ball is behind the yellow piK ball. The yellow and ltBlue cycloids are easy to distinguish. As the yellow cycloid trail shows, the piK ball began at the right side, traveling left before entering the curve, turning to approach the viewer.  

Nevyn wrote. The point of the cusp will align with the center-line of the track, and so will the top of the cycloid curve. However, all other points will be off that center-line.

Airman. Thanks, I see it now.

Nevyn wrote. My understanding is that the piK rolling on a straight section is rolling too slowly, so it drags out the cusp and it loses its point. In the curve, however, it regains that point, indicating that the curve brings it all into line so that things work correctly. It may be that the ball should be using piG rolling in straight sections, and piK rolling in curved sections on any kinematic track.

Airman. I disagree. Slow rolling on the straight track is incorrect; any point on or in the ball ‘rolls’ at exactly the same rate - none roll faster or slower. The PI = 4 app allows us to change velocities, at any velocity the curved motion distance traveled remains the same. The difference between any point on or below the rolling surface is the distance that that point travels through space. For example, the curve described by center of the rolling ball about the circular track is the shortest cycloid, a perfect circle. The curtate cycloid is shorter than the ideal cycloid. The idea of replacing the straight piK roll with the piG one is clearly wrong, they differ as per the ratio 4:3.14…  Would it be a big deal to add a little radius ball’s red marker to demonstrate?    
.

I've made tracks selectable, so you can turn them on and off. Required some refactoring of the code, but I got there in the end.

We don't need a red dot on the ball, since the lines that go around the ball already do that job. Just pick the one that starts at the bottom of the ball (I think it is the red line) and keep an eye on it.

I think you might be getting caught up in the idea that the smoother kinematic roll cusp is being caused by the point of measurement on the ball. Yes, you could cause it by doing that, but that is not what is happening in this app. The measurement point is at the ball's radius, so it is on the surface, not above or below it. So it is not the measurement point that is the problem. The only other thing is the roll itself. If the roll does not match the position changes, then the cusp is going to be smoothed out when the roll is slow, or sharpened up when the roll is fast.

We have a misunderstanding. What I’m suggesting is to extend the ball’s red marker slightly beyond the ball’s surface in order to observe the resulting cycloid.

If the point on the piK ball’s surface causes a curtate cycloid, what would be the result if we extend the the ball’s red marker slightly beyond the ball’s surface, will it go prolate or not? If so, if the cycloid begins looping instead of forming the "ideal" cycloid shape it may be the case that the ideal cycloid shape is not generated by the piK ball.      
.

I don't see what doing that tells us. We know that it will change the shape of the cusp, but we need to figure out why this app is causing that problem, not find other ways to do it. Basically, is this a programming problem, or is it a physics problem? I am leaning towards a physics problem, because there are other issues with the piK ball. The motions just aren't fluid. It slows down in the curves, which isn't so bad, but it speeds back up in a subsequent straight, which is a real problem. While the piG ball maintains a constant speed around the track and its rolling action produces the correct cycloid, even in a straight.

I'm not sold on the PI=4 idea. I am using this app to test some of it, but it isn't swaying me at the moment. So either the concept is wrong, or we have done something wrong, but I can't see what that is. It may be that pi=4 doesn't apply to rolling, because it is not something moving in a curve, but a curve in motion. That is, the balls surface is not causing the motion. It isn't like a spaceship moving in a circle where it has to apply force to cause the curve (which is what causes the difference between 3.14 and 4, as far as I can tell).

.

Nevyn wrote. I am leaning towards a physics problem, because there are other issues with the piK ball. The motions just aren't fluid. It slows down in the curves, which isn't so bad, but it speeds back up in a subsequent straight, which is a real problem.

Airman. With respect to the piK ball speeding up as it reenters a straight track, it doesn't. StevenO shared that as well as other additional information with us.

https://milesmathis.forumotion.com/t226p25-proof-that-pi4#1745

soostdijk wrote. Question: is the ball really slower? That is what most people cannot get their head around (including me   ). You mention a new "metric", but that is a bit too mainstream for me. People have been confused into thinking that there are three orthogonal axes with an arbitrary origin spanning space, but distance and time are both derived from motion, so we first have to understand motion better.

Think we have to start there by updating our understanding on momentum. The momentum of the ball seems to change instantly and is conserved around the circular motion. That is both curious.

I have also done the experiment with the 180 degree circle setup and then the exit velocity of the circular ball is 3.14/4 of the entry velocity, so the "b" momentum as you call it is then lost. It is logical as the tube cannot deliver a pushing force, only a restrictive force, but as long as we cannot show without doubt what happens with the momentum of the ball at entry and exit I will not post it. Let people absorb this experiment first.

.

I have added a multiplier property to the BallTracker class that is used on the radius to set the measurement point. A value of 1 will use the radius, as-is. A value of 1.5 would make the measurement 1 1/2 times as long as the radius. A value of 0.5, half as long. Setting it to 4/3.14 makes the kinematic track cycloid look correct on a straight section, but then the curves gets messed up.

You see, that's the problem. In the real world, the ball will be slowed down by the curve because it provides resistance. However, we do not have any resistance in our app, the ball maintains a constant velocity. But the ball still appears to slow down in the kinematic curves. Since it didn't actually lose any velocity, when it gets to a straight section again, it appears to speed up. So we get the slowing instantly, maintain that slower speed through the curve, and then get back to normal speed instantly. Under StevenO's experiment, that slowing in the curve would be gradual, happening at all points on the curve, and it would be lost after the curve.

So it may be that StevenO's experiment doesn't actually prove PI=4. It shows that the difference between PI=4 and PI=3.14 will be lost. In my example of a spaceship doing circles, the ship has to provide that turning force, which effectively adds in what StevenO's experiment loses. The ship needs to use PI=4 worth of energy. So when something is causing motion, such as a spaceship, then PI=4, but when something is just in motion, such as our ball, PI=3.14. In an orbit, gravity provides the difference between PI=4 and PI=3.14.

.

Nevyn wrote. I have added a multiplier property to the BallTracker class that is used on the radius to set the measurement point. A value of 1 will use the radius, as-is. A value of 1.5 would make the measurement 1 1/2 times as long as the radius. A value of 0.5, half as long. Setting it to 4/3.14 makes the kinematic track cycloid look correct on a straight section, but then the curves gets messed up.

Airman. Yep. Thanks for the additional information. The (4/3.14...) extended maker locations result in an ideal cycloid for the piK straight track and prolate cycloids for the rest.

Wondering about what it means.

//////\\\\\////\\\//\/\\///\\\\/////\\\\\\

P.S. First off, finding and correcting errors is always a good thing.

StevenO’s experiment didn’t reveal ball rotations, so we had to make that stuff up. Since both the piK straight and circular tracks were the same overall distance, 2*radius and 8*radius; I assumed that the number of rotations made by the two balls would be the same. This latest cycloid evidence shows that assumption was wrong. The two piK balls do not roll in synch.

The piK straight ball should roll the same number of times as is currently demonstrated by the piG straight ball. Over the 10*radius straight track I believe the piK ball will roll 5*(4/3.14…) = 6.366 rolls. Or 10/(3.14159*2*0.25) = 10/1.5708 = 6.366 rolls.

I believe the piK curved track rolling rate is correct, rolling 4 times over the course of the circular track and 2/1.5708 = 1.27 times in the initial 2*radius straight for a total number of 5.27 rotations.

With that correction we should be OK. Do you see any other necessary changes?  
.

The balls roll in sync, you can see that in your image above. The yellow and magenta balls both have their blue line at the top. The problem seems to be that the applied velocity is too fast for the roll. Alternatively, the roll is too slow for the velocity. They just don't match, but then the curve makes them match. It just seems to me that a kinematic roll doesn't work on a straight.

The kinematic and geometric straight tracks should not have the same number of rotations. For that, they would need to use the same rolling characteristic.

I have implemented a mixed roll type that uses kinematic rolling through the curves and geometric rolling in the straights.



It brings everything into line.

.

Given the piK circular track change from 5 to 5.27 ball rotations over both the short straight and circular track sections, here’s an updated remake of the pik circular track cycloids from the same two different directions I posted on 5 April.


Here are the final positions and cycloids for both the piK and piG circular tracks. Currently, both display mirror 5.27 rotation cycloid paths, the only difference between the two is the total time of travel. The yelow piK ball completes its trip in 10 seconds, while the ltBlue piG takes about 8.3 seconds, (2+2*(3.14…))/10 = 8.28 seconds.
Note the balls’ green/red intersection surface point being used to generate the cycloids, pointed roughly toward the cycloid trail starting points at the bottom of the two tracks’ red starting marker.


Here, a bit closer, the motion is paused as the yellow piK ball crosses its piG marker, the ltBlue piG ball has completed its trip.
.

.

The kinematic straight needs to be eliminated.

Nevyn wrote. The kinematic and geometric straight tracks should not have the same number of rotations. For that, they would need to use the same rolling characteristic.

I have implemented a mixed roll type that uses kinematic rolling through the curves and geometric rolling in the straights.

Airman. I absolutely agree with using “kinematic rolling in curves and geometric rolling in the straights”. According to that definition, the kinematic straight track isn’t valid, we need to use a geometric straight 10*radius long.
.

.

Here we see the PI = 4 Experiment’s two tracks, with geometric straight and kinematic curved ball motion and cycloids. The ball radius is equal to the track radius/4. The yellow ball will roll 5.27 z-rotations and the magenta ball will roll a total of 6.366 z-rotations. The motion is paused a little bit past both tracks’ pi markers. The yellow ball’s cycloid is at a zenith, 4.5 z-rotations from its starting point. The magenta ball needs to roll about 45 degrees further in order to reach its next zenith at 5.5 z-rotations from the straight track’s starting spot.


Here’s the same scene from the other side.

Nevyn, I Hope you aren’t being overcome by real world problems. Or bothered that I didn’t wait for your reply before proceeding to the next step, a major milestone, what I believe is our first accurate’ ball motion depiction of the PI = 4 Experiment.

Changing the code in order to show “kinematic rolling in curves and geometric rolling in the straights” is easy enough thank you; the ‘Kinematic straight’ ball: roll: modifier is changed from kinematic to geometric. Then I de-selected the piG straight and curved tracks from the dat GUI.

/////\\\\\/////\\\\\/////\\\\\/////

Now let’s imagine being able to vary both the track and ball radius, and provide straight and curved wave numbers (z-rotations) as a ratio. Will it agree with Miles’ Angular Velocity and Angular Momentum paper http://milesmathis.com/angle.html ?

ω = √[2r√v2 + r2) - 2r2]
r = √[ω4/(4v2 - 4ω2)]      

Thanks Chromium6. Your posting Re: https://milesmathis.forumotion.com/t119-john-gabriel-another-strict-finitist-like-mathis#6097 recommending Miles paper seemed like a good idea to me. I believe that if I was smarter I could demonstrate the validity of those two equations using this app. I'm sure I just need to give it more thought.
.

.

Last time I posted two images in which the ball radius equaled 0.25 times the track radius. Here’s a composite of four different outputs obtained by reducing the ball radius in 0.05*trkRadius increments starting from 0.2*tR to 0.05*tR as per the following chart.

The constant ratio zC/zS shouldn't have surprised me.
.

.

Angular velocity as a function of the PI = 4 track radius.

I’ve re-read and mulled over Miles’ Angular Velocity and Angular Momentum paper http://milesmathis.com/angle.html

It’s a great paper. Miles explains how to understand and calculate an orbital body’s angular velocity (ω) and tangential velocity (v) as functions of the orbital radius (r) (in meters). Angular velocity (ω) properly accounts for curved motion ‘acceleration’ and replaces the historically incorrect orbital velocity.
 
ω = √[2r√v2 + r2) - 2r2]
r = √[ω4/(4v2 - 4ω2)]
   
In my previous post, I showed a composite image of decreasing ball radii, and excel chart giving the corresponging z-rolling values. The track radius and ball velocity remained 1. Since then, using excel, for trkRadius = 1, and v=1, then ω = 0.91018 *, the chart’s central value.

This time I had hoped to show different results when the track radius and or ball velocity is varied. The PI = 4 app allows one to change the ball’s (tangential) velocity, v, and there’s nothing preventing me from varying the track radius, but the PI = 4 app does not calculate ω.

I suppose it could, but altering the PI = 4 app to try and turn it into an illustrated angular velocity calculator would be a complete deviation from Steven Oostijk’s PI = 4 experiment. That not right. Besides, Nevyn has already created a perfectly good angular velocity calculator.

https://www.nevyns-lab.com/mathis/math/graph.php?type=angular_velocity

So while I wasn’t smart enough to show how the PI = 4 app could be used to validate Miles’ angular and tangential velocity equations, having made an effort, I understand them better.

I'm not seeing how to make any additional improvements on the PI = 4 app.

* as verified on Nevyn’s angular velocity calculator.
.

That brings up and interesting point. This app essentially converts a curve into a straight by calculating its circumference (in one of two ways), and then just applies the velocity as if it was a straight. Which is the intention of the experiment, so nothing is wrong, but it does make me wonder how things would differ if we used other equations. Miles angular equations are really only good for very small things. With large things, the differences disappear (because the curves become more straight as compared to smaller things). So the radius of the curves matter. What I probably should say is that Miles' angular equations like very small radii with very large tangential velocities. That is where they shine.

.

The current suite of tracks consists of the kinematic curve (yellow ball), the geometric straight (magenta ball), and the physics violating (travels too fast by 4/3.14…) – geometric curve (ltBlue ball). In both images, the motion is paused when the geometric z-roll equals 1.5.

I like the cycloids. They literally add motion information to an otherwise static image of balls at various rotations and positions. The only “downside”, as you pointed out, the cycloids cannot be viewed from above, as in the PI = 4 App’s opening image. They need to be viewed from the side.

I haven’t messed with the code for days. I feel like the app is awaiting your final judgement. Is it still your intention to use it to illustrate Miles’ PI=4 papers?

Nevyn wrote. That brings up and interesting point. This app essentially converts a curve into a straight by calculating its circumference (in one of two ways), and then just applies the velocity as if it was a straight. Which is the intention of the experiment, so nothing is wrong, but it does make me wonder how things would differ if we used other equations. Miles angular equations are really only good for very small things. With large things, the differences disappear (because the curves become more straight as compared to smaller things). So the radius of the curves matter. What I probably should say is that Miles' angular equations like very small radii with very large tangential velocities. That is where they shine.

Airman. I think I agree, that is if when calculating the circumference “in one of two ways” you mean we can use either pi=3.14 or pi=4? What other equations do you mean?

With respect to Angular velocity, it’s easy to see, the smaller the orbital radius the better. I assume that below the electron scale the tangential velocity is likely a constant light speed.

Beyond the PI=4 app. Can you think of any follow-on apps that could build on it? Do you see any feasibility in my suggestion of creating tracks from a charged particle's (the sun) +/- 30 degrees, northern and southern charge field emission toroids?  
.

I was thinking about doing the velocity calculations in a more circular way, but after some thought, we already are. I was just trying to figure out if we could make use of Miles' velocity formula.

Yeah, the app is getting close to final. I think we need a final form. That is, we need to determine what lights are to be used, what options are we going to keep, can we use options at all? I am tempted to try to get them working for this app. Some of those are useful and I don't really want to lose them.

You could also play with the look of things. Can you make better tubes? Maybe we could add some textures to the balls, and even the tracks (if you do want to use textures, I will need to set that up since they need to come from my website, which already has plenty to use but I will need to get the code working correctly). How about the markers, can you think of another way to make them look?

We could try some flat tracks instead of tubes. Might work okay. Don't get too tied up in making it work exactly like the real experiment. We can make some changes as long as it doesn't impact the concepts it is meant to show.

I can't think of anything to build on top of this code base.

I don't understand how tracks are useful for charged particle (or planet or star) emission. What are your thoughts?

.

Viewed from the side, the kinematic curve and geometric straight balls are at their 2*radius markers.

Tracker was too similar to Track, and not descriptive enough, so I took the liberty of replacing tracker with cycloid throughout the code. I hope I didn't cause any knock on problems I might have missed.  


Working under the maxim, it’s no good making a chart unless you keep it updated, here’s the latest updated class heirarchy diagram. The BallCycloid class actually includes several additional properties left out to in order to keep this diagram simple.

Nevyn wrote. You could also play with the look of things. Can you make better tubes? Maybe we could add some textures to the balls, and even the tracks (if you do want to use textures, I will need to set that up since they need to come from my website, which already has plenty to use but I will need to get the code working correctly). How about the markers, can you think of another way to make them look?

Airman. I’d be happy to try. Yes, I recall when I down loaded the latest threejs update I was unable to ‘import’ textures from a separate file across my own directory. I believe I would need to set up some local or proxy server. Please be so kind as to set up some arrangement that would allow me to use textures.
 

Nevyn wrote. We could try some flat tracks instead of tubes. Might work okay. Don't get too tied up in making it work exactly like the real experiment. We can make some changes as long as it doesn't impact the concepts it is meant to show.

Airman. Agreed. It would be good to have different type tracks. There are many possibilities, a flat track may not be so easy as it sounds. Rails could be an alternative. Why not empty space as well?  
.

Tracker was perfectly descriptive, and cycloid is not. That class does not generate a cycloid. It tracks the position of something, hence why I called it a tracker. As it is tracking a position on the surface of a ball, it can generate a cycloid, but that is a consequence of what it is tracking, not what it does. If we switched the ball to something else, say a car, then it would not generate a cycloid anymore.

A better approach would be to make Tracker abstract, and then extend it with a BallTracker, which knows that it is tracking a point on the surface of a ball. I didn't do it that way because we don't really have any other tracker types to use.

.

Nevyn wrote. Tracker was perfectly descriptive, and cycloid is not.

Airman. Oops, thanks, another fine dose of humility. Even better, I spent several hours trying to make all the changes necessary to get back to Trackers without success. At least I’ve given the code plenty of review.

I know I should not try to recreate each and every typographical change, that just increases the likelihood of introducing new errors. I should instead undo my Git commits. Since I still don’t have enough experience or confidence undoing prior commits. I must again ask for directions. Here’s your instructions from 11 March, note that I changed them slightly to agree with the prior Commit I’d like to roll back to.

Nevyn wrote. Make sure you are on the master branch. Right-click that 'Moving circular section' 'The current default. The kinematic  ... ' commit and choose 'Reset current branch to this commit'. Then choose a Hard Reset.

Airman. Should I follow those same instructions?
.

Yeah, that is what you need to do.

You need to get use to letting Source Tree doing things for you. It saves a hell of a lot of time, and introduces some interesting things at the same time. Being able to switch between branches is one simple, but effective tool. Knowing you can completely change the code base, but be able to get back to where you were is a true gift from the programming gods.

It probably isn't a good idea to test things on a working project like this, but you can setup your own little repository and just play with things until you feel comfortable. The effort is worth it. At least it is for someone who writes code as much as I do.

.

Sorry, this isn't cooperating. I'm in the middle of my fifth try. The image shows the 'Hard Reset' result. Looking at the console source files I see the code has reverted as I would like. At this point, while on the blue highlighted Master, 'The current default ... ', when I Pull the 4, I end up right back at the top Commit 'Remove outdated js files' again.

I thought the Pull after the hard reset would discard the top 4 commits, but they haven't gone anywhere.
.

Do the reset, but don't pull the 4 commits from the server. You have to force push your local master to the server instead (overriding what it on the server). Which, now that I think about it, you may not have the privilege to do.

Hang on...

... Okay, that's fixed. You should be able to fetch and pull the new changes and be back to that commit.

Three more tries, no change from the previous results. After the hard reset, when I Fetch and Pull the 4 from the blue highlighted line 'The current default. ... ', the master label moves right back to the top Commit 'Remove outdated js files' again.

Unless you come up with a different idea, I'll leave the master as is, at the top 'Remove outdated js files.' Commit.

.

Here’s an example of balls and rails I posted from the top of this thread.

In all honesty, I think the transparent tubes work great and we don’t actually need an alternative. However, if we want, the first and easiest alternative to implement would be a dual rail track. There are two big advantages. First, we can build it from the parts already in place, instead of one tube that each ball rolls through, the rails consist of two small side-by-side tubes that the ball will roll on. There doesn’t need to be any additional support structures. Second, we use the same balls and ball motions; with some exceptions: within limits, the rail separation affects the ball’s spin rate and forward velocity, decreasing the width should increase the ball’s velocity (and decrease its spin rate) or vice-versa; and dual ball rolling contact points changes the resulting z-roll cycloids.

The biggest downside I see to creating a flat road track will involve replacing the balls with a vehicular avatar. The presumed wheels of such avatars must be accurate and somewhat independent. A road seems more complicated every time I think about it.
.

I have made the reset and pushed that to GIT, so all you should need to do is Fetch and your origin/head tag should move back to the correct commit. However, that will probably not get rid of the changes from your local repo. If that is so, then you will also need to Reset to this commit with a Hard reset in order to match what is on the remote repo. At that point, you should have no commits to push. You should not need to push anything during this operation.

.
I think I may have cancelled what you did(?). Looking at sourceTree after reading you last post I saw I needed to Push 4, I don’t know why. I did a Fetch. I don't recall needing to Pull, I would have if it indicated I needed to. I Pushed the 4. Everything is the same. I did a couple of Resets to this Commit with a Hard Reset. I get the same screen and results as I posted 0914 pm last night. While on the blue highlighted master line 'The current default. ... ', there is no option to Reset to this Commit. I went ahead and Pulled the 4 and am still on the 'Remove outdated js files’ Commit.

Please try again. 
.

I've reset it again.

When you Fetch, it will say that you need to push 4 commits, because your local repo has 4 commits that the remote repo doesn't. DO NOT PUSH THEM! Just reset your local repo to the correct commit, with hard reset, and everything should be fine. Once you reset, the 4 commits to be pushed should go away and you will not have anything to push.

.
That worked, the top is now the 'The current default. ... ' Commit. Thanks.
.

This is why we do serious changes on a separate branch. It is much easier to not merge, than it is to roll things back.

.

Viewing the under side, the kinematic curve and geometric straight balls are again at their 2*radius markers.


Showing my first working branch and repository, AmnMods. And a new but familiar node ‘Removing the no longer needed js file.’ (piEq4Functions) to verify it worked.  

Nevyn wrote. This is why we do serious changes on a separate branch. It is much easier to not merge, than it is to roll things back.

Airman. Thanks for your patience and persistence Nevyn. See, I can eventually get the hint, I suppose I’m better at following orders. After reviewinga few youtube videos I took the plunge. My own personal branch and branch repository. I suppose that when I accrue a task’s worth of nodes along with your review/approval I’ll Push those changes to the Master. Of course we’ll need to discuss it first as I don't think I've seen that particular video yet.

You suggested improving the markers or optimizing lights or whatever. Ah, I see there's an error with changing aLight.color from the dat GUI. A few easy tasks like that sounds like a good way to get familiar with your new and improved code, before attempting anything more serious.
.

While there are many different ways to use GIT and its Branches, I tend to think of a branch as the Research and Development department. You don't want R&D going straight into production. You want to make sure that it works correctly, find any little issues, and sort them out before you start making changes to the production line (master being the production line in this metaphor).

When I suggested you try a few different track types, I wasn't thinking about changing the way motion is handled, or the balls, or anything other than the way the track looks. Just its visuals, nothing else. We don't need to use a car because we have a flat track. We just want a track that is flat and the ball will still travel on its current path.

While I do like the idea of 2 rails that the balls move along, that would look cool and give it a steam-punk kind of feel, I think that will be much harder than doing a flat track. You would have to think about the differences in length of each rail as it moves around a curve. Possible, not even really that difficult, just a bit more complicated than something flat.

By the way, I don't want to lose the tubes. I just want more options for the way the tracks look. I will probably need to figure out a way to make that configurable.

.

"Simulated planer tracks".

Nevyn wrote. When I suggested you try a few different track types, I wasn't thinking about changing the way motion is handled, or the balls, or anything other than the way the track looks. Just its visuals, nothing else. We don't need to use a car because we have a flat track. We just want a track that is flat and the ball will still travel on its current path.

Thanks for the clarification. I was already lost (easily done), wondering what motion changes - including momentum and friction (my thoughts do get carried away) - are necessary for alternative tracks. If the ball and its motions are to remain the same, and a different track type amounts to nothing more than a visual change, I can forget all that. A flat road must be our first alternative, or a bare plane table top as I included in a previous Pi = 4 app version. The markers can be shallow rectangular boxes flush with the bottom of the ball or we use the current markers and suggest/describe them as standalone hoops or croquet wickets, that the balls will roll through.

For the time being, and something to look at, the image includes a used table. The tubes are completely transparent. The markers are two-sided; the marker colors aren’t right because I used the ambient light’s color to make a quick and dirty table color. The markers could benefit from a little more thickness. I’m not happy with the ambient light or the spotlights, they ‘cast shadows’ but it doesn’t look like it. I suppose a ‘paved’ or otherwise distinguishable roadbed would be better than a bare plane table top.  

I have no idea how you would proceed in creating alternative tracks. I guess I'd begin in the StraightSection and CurvedSection prototype.init functions. I’d comment out ( // ) the current straight and curved sections’ tube and torus geometries, and replace them with very long wide and shallow boxlike geometries and material), straight and curved sections. I'd find some way to include them both and switch between them, if it was promising enough, later.  

Branches, I like the R&D approach/philosophy. What's the working process? Am I supposed to let you know (via email or mention it here in a post? Perhaps an announcement Commit? ) when I’d like to Push my latest to the master repository? For example, I have three Commits: an update, a cleanup and an error fix ready and waiting. As the project lead, you are responsible for checking out and verifying my Commits and deciding when to initiate Pull requests? Or do I initiate the Pull request? 
.

Generally, a developer works on a branch, tests it, and when they are happy that it works, they create a Pull Request. Part of the Pull Request is a list of reviewers, who will be notified to look at the code changes and make any comments about them such as suggested changes. That is all done through the BitBucket web site, not Source Tree (or Fork, if you are using that). However, since this is a team of only two, we can just communicate the desire to merge a branch or have it reviewed. I don't mind either way.

.

Flat tracks, a ball radius wide.

Track update. We have an alternative to the transparent tubes, flat tracks a ball radius wide. A couple of problems made for questionable progress.

1. The scene center is a ball radius lower for the flat tracks than the tube tracks. With tube tracks, the center of the scene and the center of the straight track ball will intersect at the center of the 10*track radius. With flat tracks, to prevent the track from intersecting the ball, the path mesh is lowered (by half the straight box height and a ball radius). Halfway along and on the straight path’s surface lies the scene center. The sTrk ball passes over the scene center like old road kill. Is that a problem? Since I brought it to your attention I'll assume not unless you say otherwise.

2. The straight flats are shallow boxes. The circular path is a two sided torus; the straight path appears more solid while the curved paths have a surface comprised like wire mesh with plenty of openings. I haven’t tried it yet, I’ll probably go ahead and replace the toruses with Ring Buffer Geometry objects.
.

.

Flat tracks, a ball radius wide, continued.

Track update. Ok, I’d say we now have a proper alternative to the transparent tubes, flat tracks.

The straight section tracks’ box geometry top surfaces are flush against the bottom of either the scene or the rolling balls. The ball surface markers’ radii are greater than the ball radius and so the ball markers penetrate the track surfaces and track markers. The curved tracks are 2D, ring geometry; the circular tracks’ y-axis vertical heights equal 0. In order to avoid aliasing, or visual interference patterns between overlapping straight and circular tracks, the top surface of the circular tracks are not flush with the bottom of the scene and straight ball. The circular tracks are lowered halfway down the straight path box geometry’s y-axis height below the rolling balls. Reduce the box height to bring the curved track top surface and bottom of the ball as close together as you’d like.  

Both the transparent tubes and flat tracks share the exact same motions. I can think of no others. All my track imaginings involved motion changes. The dual rails I’d mentioned involve replacing the single cycloid with dual curtate cycloids at a higher spin rate. Without that motion change I cannot suggest including dual rails as an alternative.

There’s one alternative I’d most strongly suggest, involving the simplest motion change I can think of – the balls’ spin direction. The no track alternative. Remove the track (let the track markers remain) and let the balls spin through space on their current paths. Replace the rollGroup’s top surface z-roll with an x-spin orthogonal to the balls’ forward direction. I'm hoping the change might be that simple. We might allow changing the spin rate, let the cycloids become spiraling coils.


P.S. Here's a close-up view of the straight/circular tracks vertical positioning. The three balls are approaching the tracks' zero mark, note the small ledge or drop to the curved tracks.
.