PI NINE - Pi experiment with two edge track
4 posters
Page 1 of 1
 PI NINE - Pi experiment with two edge track
PI NINE - Pi experiment with two edge track
.
Miles has a new PI paper. Peter conducted the PI experiment and found the circular track ball traveled not 4, but closer to pi, at 3.3. This is a negative experimental finding that Miles must explain. Please go read Miles’ paper and see Peter’s video without any further ado, (Miles will ask you to figure out why).
http://milesmathis.com/updates.html
NEW PAPER, added 1/30/21, A Pi Test. , http://milesmathis.com/pi9.pdf. A reader gives us a new pi experiment to unwind.
///\\\\/////\\\\\\///////\\\\\\\\///////\\\\\\/////\\\\///
Unlike Steven Oostdijk’s pvc tubing, Peter has assembled a professionally milled metal track with 3/8” square-cut ball track. The ball is 3/4” diameter. The diameter of the track is 10”.
Miles explains the error in terms of ‘constraint’ and ‘forward freedom’. Please overlook my errors and accept this image if it might be of any aid in your own analysis.

.
Miles has a new PI paper. Peter conducted the PI experiment and found the circular track ball traveled not 4, but closer to pi, at 3.3. This is a negative experimental finding that Miles must explain. Please go read Miles’ paper and see Peter’s video without any further ado, (Miles will ask you to figure out why).
http://milesmathis.com/updates.html
NEW PAPER, added 1/30/21, A Pi Test. , http://milesmathis.com/pi9.pdf. A reader gives us a new pi experiment to unwind.
///\\\\/////\\\\\\///////\\\\\\\\///////\\\\\\/////\\\\///
Unlike Steven Oostdijk’s pvc tubing, Peter has assembled a professionally milled metal track with 3/8” square-cut ball track. The ball is 3/4” diameter. The diameter of the track is 10”.
Miles explains the error in terms of ‘constraint’ and ‘forward freedom’. Please overlook my errors and accept this image if it might be of any aid in your own analysis.

.
Last edited by LongtimeAirman on Wed Feb 03, 2021 9:13 pm; edited 1 time in total (Reason for editing : 3/8” square-cut ball)
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
Chromium6 likes this post
 Re: PI NINE - Pi experiment with two edge track
Re: PI NINE - Pi experiment with two edge track
Quoting A Pi Test,
Airman Here’s a python code track area calculation for Peter’s tracks.
The output:
STkCLength: 40 in, TrackWidth: 0.375 in
CTkRadius: 10 in, CTkOutRadius: 10.1875 in, CTkInRadius: 9.8125 in
StTrkArea: 15.0 sqIn, CTrkArea: 23.561944901923425 sqIn
.
Miles wrote. As one final hint, notice that compared to Steven's balls, the ball in the curve here is going faster. It gets around the track about 21% faster than Steven's circle ball (relative to the straight ball). Ask yourself why it would do that.
It does that because the curved track has far more freedom to move than the straight one in the same experiment. To say it another way, it constrains the ball far less.
Miles wrote. You can also calculate this by calculating the total area of the curved track versus an equal length of straight track. The curved track has a much greater area.
Airman Here’s a python code track area calculation for Peter’s tracks.
- Code:
# This python program calculates both the straight and curved
# 3/8" square-cut areas defining the balls' contact points.
# Measurements are in inches.
import math
TrackWidth = 0.375
STkCLength = 40
CTkRadius = 10
CTkOutRadius = CTkRadius + (TrackWidth/2)
CTkInRadius = CTkRadius - (TrackWidth/2)
print("STkCLength:", STkCLength, "in, TrackWidth:", TrackWidth, "in")
print("CTkRadius:", CTkRadius, "in, CTkOutRadius:", CTkOutRadius, "in, CTkInRadius:", CTkInRadius, "in")
StTrkArea = TrackWidth * STkCLength
CTrkArea = math.pi * (CTkOutRadius * CTkOutRadius) - math.pi * (CTkInRadius * CTkInRadius)
print("StTrkArea:", StTrkArea, "sqIn, CTrkArea:", CTrkArea, "sqIn")
The output:
STkCLength: 40 in, TrackWidth: 0.375 in
CTkRadius: 10 in, CTkOutRadius: 10.1875 in, CTkInRadius: 9.8125 in
StTrkArea: 15.0 sqIn, CTrkArea: 23.561944901923425 sqIn
.
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
Chromium6 likes this post
 Re: PI NINE - Pi experiment with two edge track
Re: PI NINE - Pi experiment with two edge track
I almost got the explanation but did not, so i had read Miles's
I did see the ball was going faster in the circular track, seeming to speed up even.
Regards,
Daniel
I did see the ball was going faster in the circular track, seeming to speed up even.
Regards,
Daniel
D_Archer- Posts : 7
Join date : 2014-10-27
Chromium6 likes this post
 Re: PI NINE - Pi experiment with two edge track
Re: PI NINE - Pi experiment with two edge track
.
Hi Daniel.
I didn't get it. Greater freedom in the curve, bends my mind, still trying to understand.
Perhaps thinner tracks might approach pi=4? I modified yesterday’s python program to accept alternate track widths.
Continued TrackWidth divisions by 10 result in the same area ratio, equal to geometric pi/2. Pi=4 for single contact point tubes, but not for dual contact point tracks, regardless of the distance between the two points.
I have another possible explanation I don't recall Miles mentioning. Assuming good rolling contact, at all points along the circular track the dual contact points constrain the direction of the ball’s axis of rotation. A single contact point cannot constrain the direction of the ball’s axis of rotation, in which case curved motion alone must cause that change - which slows the ball down to pi=4.
.
Hi Daniel.
I didn't get it. Greater freedom in the curve, bends my mind, still trying to understand.
Perhaps thinner tracks might approach pi=4? I modified yesterday’s python program to accept alternate track widths.
- Code:
# This program calculates both the straight and curved areas defined by the balls' contact points.
# Starting with a track width of 3/8, enter new trackwidths if desired, the program stops with 0.
# Measurements are in inches.
import math
TrackWidth = 0.375
while TrackWidth > 0:
STkCLength = 40
CTkRadius = 10
CTkOutRadius = CTkRadius + (TrackWidth/2)
CTkInRadius = CTkRadius - (TrackWidth/2)
print("STkCLength:", STkCLength, "in, TrackWidth:", TrackWidth, "in")
print("CTkRadius:", CTkRadius, "in, CTkOutRadius:", CTkOutRadius, "in, CTkInRadius:", CTkInRadius, "in")
StTrkArea = TrackWidth * STkCLength
CTrkArea = math.pi * (CTkOutRadius * CTkOutRadius) - math.pi * (CTkInRadius * CTkInRadius)
CAToSARatio = CTrkArea/StTrkArea
print("StTrkArea:", StTrkArea, "sqIn, CTrkArea:", CTrkArea, "sqIn")
print("CAToSARatio:", CAToSARatio)
print("" )
print("Please enter new TrackWidth. 0 stops the program" )
TrackWidth = float(input("New TracKWidth: "))
Output:
STkCLength: 40 in, TrackWidth: 0.375 in
CTkRadius: 10 in, CTkOutRadius: 10.1875 in, CTkInRadius: 9.8125 in
StTrkArea: 15.0 sqIn, CTrkArea: 23.561944901923425 sqIn
CAToSARatio: 1.570796326794895
Please enter new TrackWidth. 0 stops the program
New TracKWidth: 0.1
STkCLength: 40 in, TrackWidth: 0.1 in
CTkRadius: 10 in, CTkOutRadius: 10.05 in, CTkInRadius: 9.95 in
StTrkArea: 4.0 sqIn, CTrkArea: 6.283185307179679 sqIn
CAToSARatio: 1.5707963267949197
Continued TrackWidth divisions by 10 result in the same area ratio, equal to geometric pi/2. Pi=4 for single contact point tubes, but not for dual contact point tracks, regardless of the distance between the two points.
I have another possible explanation I don't recall Miles mentioning. Assuming good rolling contact, at all points along the circular track the dual contact points constrain the direction of the ball’s axis of rotation. A single contact point cannot constrain the direction of the ball’s axis of rotation, in which case curved motion alone must cause that change - which slows the ball down to pi=4.
.
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
Chromium6 likes this post
 Re: PI NINE - Pi experiment with two edge track
Re: PI NINE - Pi experiment with two edge track
.
Yesterday I wrote. I have another possible explanation I don't recall Miles mentioning. Assuming good rolling contact, at all points along the circular track the dual contact points constrain the direction of the ball’s axis of rotation. A single contact point cannot constrain the direction of the ball’s axis of rotation, in which case curved motion alone must cause that change - which slows the ball down to pi=4.
I gave my comment more thought, expanded it a bit and include a diagram for clarity.
The track with dual edges constrains the rolling ball in two ways. 1, by maintaining the ball’s distance from the track center axis as well as 2. slowly torqueing the rolling ball’s spin axis, always keeping the ball’s spin axis pointed to the circle track’s center axis; since the ball isn’t torqueing itself, it will not slow down in the curve and will not display proper curved motion. The tube track with only a single contact point along the track centerline can only constrain the ball’s distance to the track center, but the centerline cannot torque the ball’s spin axis, the ball must torque itself, with a resulting velocity change and experimental result of pi=4 .

I'll try sending Miles an email.
Thanks Cr6. Now I need to do the diagram in python too.
.
Yesterday I wrote. I have another possible explanation I don't recall Miles mentioning. Assuming good rolling contact, at all points along the circular track the dual contact points constrain the direction of the ball’s axis of rotation. A single contact point cannot constrain the direction of the ball’s axis of rotation, in which case curved motion alone must cause that change - which slows the ball down to pi=4.
I gave my comment more thought, expanded it a bit and include a diagram for clarity.
The track with dual edges constrains the rolling ball in two ways. 1, by maintaining the ball’s distance from the track center axis as well as 2. slowly torqueing the rolling ball’s spin axis, always keeping the ball’s spin axis pointed to the circle track’s center axis; since the ball isn’t torqueing itself, it will not slow down in the curve and will not display proper curved motion. The tube track with only a single contact point along the track centerline can only constrain the ball’s distance to the track center, but the centerline cannot torque the ball’s spin axis, the ball must torque itself, with a resulting velocity change and experimental result of pi=4 .

I'll try sending Miles an email.
Thanks Cr6. Now I need to do the diagram in python too.
.
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
Chromium6 likes this post
 Re: PI NINE - Pi experiment with two edge track
Re: PI NINE - Pi experiment with two edge track
Call me crazy but at the atom to atom level are we still seeing the manhatten metric? Is there ever a perfect curve in the real world-nature?
For example if the ring was only one atom thick and the "ball" was like 7 atoms round... would it roll at 4 PI?
For example if the ring was only one atom thick and the "ball" was like 7 atoms round... would it roll at 4 PI?
Chromium6- Posts : 818
Join date : 2019-11-29
 Re: PI NINE - Pi experiment with two edge track
Re: PI NINE - Pi experiment with two edge track
.
You lost me Cr6, size has nothing to do with it. The question is, do we have proper curved motion, or not?
Reiterating, assuming a good rolling contact, in Peter’s experiment, the track is a 3/8” wide slot with inside and outside edges. I’m asserting that the mere presence of those two edges provides all the force necessary to change the ball’s spin direction and so pi approaches 3.14… .
In Steven’s tube, the ball must remain on track, yet the track cannot provide any force necessary to change the direction of the ball’s spin. The ball must constantly torque itself, with a velocity reduction showing pi=4.
Orbital motion, with a large central body and small orbiting satellite is like the tube track. The orbital velocity, gravity and charge determine the orbital radius, the body wants to align itself to the orbital center, but apparently gravity and charge cannot torque the orbiting body. The body torques itself and pi=4.
Only motion, and constraints are involved.
I'm not certain, I'll keep thinking about it.
.
You lost me Cr6, size has nothing to do with it. The question is, do we have proper curved motion, or not?
Reiterating, assuming a good rolling contact, in Peter’s experiment, the track is a 3/8” wide slot with inside and outside edges. I’m asserting that the mere presence of those two edges provides all the force necessary to change the ball’s spin direction and so pi approaches 3.14… .
In Steven’s tube, the ball must remain on track, yet the track cannot provide any force necessary to change the direction of the ball’s spin. The ball must constantly torque itself, with a velocity reduction showing pi=4.
Orbital motion, with a large central body and small orbiting satellite is like the tube track. The orbital velocity, gravity and charge determine the orbital radius, the body wants to align itself to the orbital center, but apparently gravity and charge cannot torque the orbiting body. The body torques itself and pi=4.
Only motion, and constraints are involved.
I'm not certain, I'll keep thinking about it.
.
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
 Re: PI NINE - Pi experiment with two edge track
Re: PI NINE - Pi experiment with two edge track
No problem LTAM I presented this out of context of the example. I was thinking in terms of atoms side by side for 1 track. But dynamics with 2 tracks or 3 tracks etc., until most surface area of the ball is touched. I was thinking a 1 atom track with a primitive shaped ball would have the manhatten metric demonstrated as it rolled?
Chromium6- Posts : 818
Join date : 2019-11-29
 Re: PI NINE - Pi experiment with two edge track
Re: PI NINE - Pi experiment with two edge track
.
One more try.
In order to display proper pi=4 curved motion, an object must be subject to two simultaneous motions, and not just any two motions. Perhaps the simplest example – in the absence of all other forces, an object with two constant, linear velocities: 1. forward and 2. orthogonal; will travel in a circular path.
The ball in the pi=4 circular track experiences two spin motions. 1. Rolling (or spinning). While moving forward, the ball spins about its own internal spin axis; and 2. The traveling ball is also rotating about the track’s center axis.
As far as rolling goes, let the ball be radius 1, the circumference is then 2*(geometric pi). Sure, we know that all points (or atoms) on the rim of a wheel (or a contact belt on a sphere) describe cycloid paths where the distance traveled by the surface points prove pi=4. That’s true for the ball rolling along the pi=4 straight track and its true at any scale. With respect to the pi experiment, we need only recognize that the ball rolling about its central spin axis has inertia. Given the freedom, the rolling ball would continue to roll in a straight line. It takes force to change the rolling ball’s direction (or spin axis).
The circular track ball with both spin motions constantly keeps its spin axis pointed to the circular track center axis.
To the best of my knowledge, all the above is a true and accurate description of the pi=4 experiment as I understand it. Nothing original, just my perspective. I suppose I should add I’ve spent many hours doing Steven's tube experiment (unsuccessfully) as well as developing 3 different threejs pi=4 simulations, not entirely unsuccessfully.
All I’m trying to add is my belief that a dual edge slot track, or any rail track cannot be used to show that pi=4. The track negates one of the ball motions - rotation around the circular track center. Even in the curve, those two edge tracks constantly redirect the ball forward. The spinning ball doesn't need to spend energy to reorient its internal spin axis, the track alone changes the direction of the ball, in which case pi=(geometric pi).
.
One more try.
In order to display proper pi=4 curved motion, an object must be subject to two simultaneous motions, and not just any two motions. Perhaps the simplest example – in the absence of all other forces, an object with two constant, linear velocities: 1. forward and 2. orthogonal; will travel in a circular path.
The ball in the pi=4 circular track experiences two spin motions. 1. Rolling (or spinning). While moving forward, the ball spins about its own internal spin axis; and 2. The traveling ball is also rotating about the track’s center axis.
As far as rolling goes, let the ball be radius 1, the circumference is then 2*(geometric pi). Sure, we know that all points (or atoms) on the rim of a wheel (or a contact belt on a sphere) describe cycloid paths where the distance traveled by the surface points prove pi=4. That’s true for the ball rolling along the pi=4 straight track and its true at any scale. With respect to the pi experiment, we need only recognize that the ball rolling about its central spin axis has inertia. Given the freedom, the rolling ball would continue to roll in a straight line. It takes force to change the rolling ball’s direction (or spin axis).
The circular track ball with both spin motions constantly keeps its spin axis pointed to the circular track center axis.
To the best of my knowledge, all the above is a true and accurate description of the pi=4 experiment as I understand it. Nothing original, just my perspective. I suppose I should add I’ve spent many hours doing Steven's tube experiment (unsuccessfully) as well as developing 3 different threejs pi=4 simulations, not entirely unsuccessfully.
All I’m trying to add is my belief that a dual edge slot track, or any rail track cannot be used to show that pi=4. The track negates one of the ball motions - rotation around the circular track center. Even in the curve, those two edge tracks constantly redirect the ball forward. The spinning ball doesn't need to spend energy to reorient its internal spin axis, the track alone changes the direction of the ball, in which case pi=(geometric pi).
.
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
Chromium6 likes this post
 Re: PI NINE - Pi experiment with two edge track
Re: PI NINE - Pi experiment with two edge track
.
Miles updated http://milesmathis.com/pi9.pdf last week.
I cogitated and studied it further. I feel certain I understand and agree with most everything he describes.
Steven’s circular tube (flat) track allows the ball to roll along the line where gravity and centripetal forces balance.
The ball travelling along Peter’s dual edge circular track will always feel a greater centripetal force where it meets the track’s outside edge. That contact line, some width beyond a flat track’s ideal rolling line for that particular experimental setup, creates a differential resulting in greater freedom in the curve, because of that, the ball travels faster in the dual edge curved track than in the tube’s curved track.
I’m grateful for the additional reader’s (professional engineer!) analysis, his work looks good to me. I admit I’ve made quite a few simplifying (false) assumptions concerning circular dual edge tracks in the past, like discounting centripetal force. I’m aware that the dual edges change the ball’s effective rolling radius. In the https://milesmathis.forumotion.com/t554p375-animate-the-pi-4-experiment#6225 thread last may, I show how I needed to increase the dual edge rail track ball size to match its cycloid/rolling radius with the cycloid/rolling radius of the ball rolling in the tube track. The engineer indicated he believes there’s a constant sliding friction involved and I agree.
I believe Miles has left out an important fact. As I said above, the ball in Steven’s circular tube track is performing two motions, rolling and rotating its rolling axis about the circular track center. The ball must torque itself around the circle track center axis and Pi=4. The ball in Peter’s circular dual edge track is – to some extent, not completely, forced to turn along the dual track’s outside edge, creating increased friction and ball slowdown. Pi is somewhere between 3.14 and 4.
Miles mentioned banking the circular track’s dual edges, (apparently to match the tube results and Pi=4!?) as a bit too expensive. I don’t believe the dual edge track can be used to prove Pi=4. Even roughly banking the dual edges such that they straddle the ideal line, allowing the ball to feel roughly equal gravitational and centripetal forces along both rails would certainly better match the dual edge straight track. In that case I believe the dual edge track will do a better job of constantly changing the rolling ball’s direction, so that the rolling ball will torque itself as little as possible, and so Pi approaches 3.14.
.
Miles updated http://milesmathis.com/pi9.pdf last week.
I cogitated and studied it further. I feel certain I understand and agree with most everything he describes.
Steven’s circular tube (flat) track allows the ball to roll along the line where gravity and centripetal forces balance.
The ball travelling along Peter’s dual edge circular track will always feel a greater centripetal force where it meets the track’s outside edge. That contact line, some width beyond a flat track’s ideal rolling line for that particular experimental setup, creates a differential resulting in greater freedom in the curve, because of that, the ball travels faster in the dual edge curved track than in the tube’s curved track.
I’m grateful for the additional reader’s (professional engineer!) analysis, his work looks good to me. I admit I’ve made quite a few simplifying (false) assumptions concerning circular dual edge tracks in the past, like discounting centripetal force. I’m aware that the dual edges change the ball’s effective rolling radius. In the https://milesmathis.forumotion.com/t554p375-animate-the-pi-4-experiment#6225 thread last may, I show how I needed to increase the dual edge rail track ball size to match its cycloid/rolling radius with the cycloid/rolling radius of the ball rolling in the tube track. The engineer indicated he believes there’s a constant sliding friction involved and I agree.
I believe Miles has left out an important fact. As I said above, the ball in Steven’s circular tube track is performing two motions, rolling and rotating its rolling axis about the circular track center. The ball must torque itself around the circle track center axis and Pi=4. The ball in Peter’s circular dual edge track is – to some extent, not completely, forced to turn along the dual track’s outside edge, creating increased friction and ball slowdown. Pi is somewhere between 3.14 and 4.
Miles mentioned banking the circular track’s dual edges, (apparently to match the tube results and Pi=4!?) as a bit too expensive. I don’t believe the dual edge track can be used to prove Pi=4. Even roughly banking the dual edges such that they straddle the ideal line, allowing the ball to feel roughly equal gravitational and centripetal forces along both rails would certainly better match the dual edge straight track. In that case I believe the dual edge track will do a better job of constantly changing the rolling ball’s direction, so that the rolling ball will torque itself as little as possible, and so Pi approaches 3.14.
.
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
Chromium6 likes this post
 Re: PI NINE - Pi experiment with two edge track
Re: PI NINE - Pi experiment with two edge track
.
Please consider these Steven Oostdijk comments from another thread, Proof that pi=4 on Tue Nov 08, 2016.
https://milesmathis.forumotion.com/t226p25-proof-that-pi4#1745
Later that day
Airman. Steven’s comments provide many insights and make an excellent reference, plus food for thought, humble pie. Steven identifies the main distinguishing characteristic of the tube track, “the tube cannot deliver a pushing force, only a restrictive force”. Restrictive force is what the floor you are standing on provides to counter your weight, the floor is a limit to your downward motion. The tube constrains the rolling ball to remain within the tube with only a single contact point along a track path. One might ask, how the heck does the rolling ball rotate its spin axis direction about the center of the curved tube track? There’s a very good answer, precession. Demonstrated and explained by Professor Walter Lewin in one of his lectures, Rolling Motion, Gyroscopes, VERY NON-INTUITIVE. Yes, I posted this before, it’s a great lecture.
At around 22 minutes in, Professor Lewin is using both hands holding the axil of a spinning bicycle wheel in front of himself. The circumference is rolling out and away from his face – like watching a ball rolling forward from behind. He explains how turning one side of the axil slightly down, and the other end of the axil slightly up results in a rotation of the wheel’s spin axis in a horizontal plane. At 23:23 he spins the chair he is sitting on by applying that steering wheel torque to the wheel’s spin axis. The spin axis turns to the direction of the torque, left or right, motion as a result of torque, precession.
As Miles describes, the ball in the curved track will make a contact path where gravity and centripetal force of the rolling ball balance, at some height up the wall of the tube’s inside surface. Just like that bicycle wheel, banking the rolling contact point up the wall in the curve creates a torque which rotates the ball’s spin axis in a plane about the circular track center. The height of the ball’s path is determined by the ball’s mass, velocity, and radius, and the circular track radius (or curvature).
Now we might better appreciate how the dual edge track works, the ball is not free to move to a balanced path, the circular dual edges prevents the ball from changing its own direction gyroscopically. The ball feels different forces at each of the two track edges depending on centripetal force and gravity. As the ball attempts to roll forward in a straight line, the track will make a sliding contact just ahead of the ball’s current contact point on the track’s outside edge. As the ball advances, the encroaching outside edge meets the ball ahead of the current ball contact point, exerting an increasing force up to Fc=mRp ω ^2. This frictional sliding force is what constantly changes the direction of the rolling ball about the circular track center. Generally, the ball in the curved dual edge track starts fast and gradually slows throughout. Completely unlike the ball in the tube track hitting each marker like clockwork.
P.S. Below, left side, is a precession question Prof Lewin asks, then demonstrates during his lecture. Given a wheel with spin axis L, apply the up and down (+/-z direction) forces F, which create the torque T in the direction of the positive y axis. What is the resulting change in the wheel's spin axis? My answer is on the right, the wheel's spin axis rotates in the horizontal plan, toward the direction of the applied torque, counter clockwise when viewed from above. The same forces apply to a ball rolling through the circular tube track, enabling it to rotate its spin axis about the circular track center.
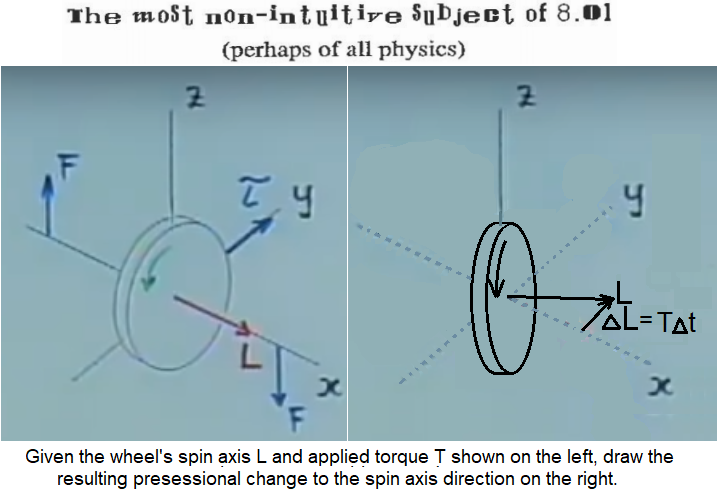
.
Please consider these Steven Oostdijk comments from another thread, Proof that pi=4 on Tue Nov 08, 2016.
https://milesmathis.forumotion.com/t226p25-proof-that-pi4#1745
soostdijk wrote.
Question: is the ball really slower? That is what most people cannot get their head around (including me ). You mention a new "metric", but that is a bit too mainstream for me. People have been confused into thinking that there are three orthogonal axes with an arbitrary origin spanning space, but distance and time are both derived from motion, so we first have to understand motion better.
Think we have to start there by updating our understanding on momentum. The momentum of the ball seems to change instantly and is conserved around the circular motion. That is both curious.
I have also done the experiment with the 180 degree circle setup and then the exit velocity of the circular ball is 3.14/4 of the entry velocity, so the "b" momentum as you call it is then lost. It is logical as the tube cannot deliver a pushing force, only a restrictive force, but as long as we cannot show without doubt what happens with the momentum of the ball at entry and exit I will not post it. Let people absorb this experiment first.
Later that day
soostdijk wrote.
There is two things I could suggest to mention in the discussion:
1. Pulling a "velocity" around a circle is not the same as pulling a solid ruler around a circle. The velocity vector will need to be rotated along the path otherwise it would not follow the path. This rotation takes time. So it would not be logical that the length of a circular path measured with a velocity would be the same as measured with a ruler. For all these people shouting that Pi will always remain 3.14, sure, but only for geometric ratios.
2. There was a discussion whether the definition of length would need to change but that is not the case. Measuring the length of the circular path starting with the origin on the path will yield 4 as is shown in the video. It would yield 3.14 measured from the virtual center but only if you ignore the rotating reference frame of the ball (which is interestingly enough actually admitted by the mainstream ).
Airman. Steven’s comments provide many insights and make an excellent reference, plus food for thought, humble pie. Steven identifies the main distinguishing characteristic of the tube track, “the tube cannot deliver a pushing force, only a restrictive force”. Restrictive force is what the floor you are standing on provides to counter your weight, the floor is a limit to your downward motion. The tube constrains the rolling ball to remain within the tube with only a single contact point along a track path. One might ask, how the heck does the rolling ball rotate its spin axis direction about the center of the curved tube track? There’s a very good answer, precession. Demonstrated and explained by Professor Walter Lewin in one of his lectures, Rolling Motion, Gyroscopes, VERY NON-INTUITIVE. Yes, I posted this before, it’s a great lecture.
At around 22 minutes in, Professor Lewin is using both hands holding the axil of a spinning bicycle wheel in front of himself. The circumference is rolling out and away from his face – like watching a ball rolling forward from behind. He explains how turning one side of the axil slightly down, and the other end of the axil slightly up results in a rotation of the wheel’s spin axis in a horizontal plane. At 23:23 he spins the chair he is sitting on by applying that steering wheel torque to the wheel’s spin axis. The spin axis turns to the direction of the torque, left or right, motion as a result of torque, precession.
As Miles describes, the ball in the curved track will make a contact path where gravity and centripetal force of the rolling ball balance, at some height up the wall of the tube’s inside surface. Just like that bicycle wheel, banking the rolling contact point up the wall in the curve creates a torque which rotates the ball’s spin axis in a plane about the circular track center. The height of the ball’s path is determined by the ball’s mass, velocity, and radius, and the circular track radius (or curvature).
Now we might better appreciate how the dual edge track works, the ball is not free to move to a balanced path, the circular dual edges prevents the ball from changing its own direction gyroscopically. The ball feels different forces at each of the two track edges depending on centripetal force and gravity. As the ball attempts to roll forward in a straight line, the track will make a sliding contact just ahead of the ball’s current contact point on the track’s outside edge. As the ball advances, the encroaching outside edge meets the ball ahead of the current ball contact point, exerting an increasing force up to Fc=mRp ω ^2. This frictional sliding force is what constantly changes the direction of the rolling ball about the circular track center. Generally, the ball in the curved dual edge track starts fast and gradually slows throughout. Completely unlike the ball in the tube track hitting each marker like clockwork.
P.S. Below, left side, is a precession question Prof Lewin asks, then demonstrates during his lecture. Given a wheel with spin axis L, apply the up and down (+/-z direction) forces F, which create the torque T in the direction of the positive y axis. What is the resulting change in the wheel's spin axis? My answer is on the right, the wheel's spin axis rotates in the horizontal plan, toward the direction of the applied torque, counter clockwise when viewed from above. The same forces apply to a ball rolling through the circular tube track, enabling it to rotate its spin axis about the circular track center.

.
Last edited by LongtimeAirman on Fri Feb 26, 2021 12:55 pm; edited 2 times in total (Reason for editing : added P.S.)
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
Chromium6 likes this post
 Re: PI NINE - Pi experiment with two edge track
Re: PI NINE - Pi experiment with two edge track
.
Reporting some possible progress.
Happy belated Pi day, March 14, or is it the zeroth of April, the day before April fools day?
You might notice a change or two. My old machine died unexpectedly of a hard drive problem. The new machine is quite a bit different. Needless to say, it’s like starting all over again, my psyche may never recover.
Last time, I described Prof Lewin showing us how he uses both arms to torque a spinning bicycle wheel by its axle (that’s better spelling than last time) left or right like some kind of a steering wheel in order to turn the direction of the swivel seat he is sitting on. I said that’s how the ball in the circular tube track precesses. Well, Prof Lewin’s next precession demonstration uses the same spinning bicycle wheel suspended by a single point, applicable to the ball in the circular tube track. Suspend the spinning wheel by either the left or the right ends of the axle. The youtube image in my prior post shows a view of the spinning wheel along the axle, or spin axis, or L, or the direction of the spin angular momentum.
Here’s a slightly cleaned up blackboard diagram of the suspended spinning wheel Prof Lewin draws during the video.

Of course the spinning wheel as shown doesn’t flop over, as the wheel spins it will continually precess or orbit about the suspension point due to the constant force of gravity – increasing the weight increases the precession speed.

The large diagram above shows how I believe the ball in the circular tube track is effectively ‘suspended’ while traveling along the path balanced between centripetal and gravitational forces, up a bit on the tube’s outside wall. The spin axis is constantly chasing the torgue around the circular track. I’m still wondering whether the straight line between the ball/tube contact point, and the ball center is created by Fc and the mg vectors as shown is what creates the outside path or not.
P.S. After giving it some more thought, I’ve made a few changes to the previous diagram as shown below.
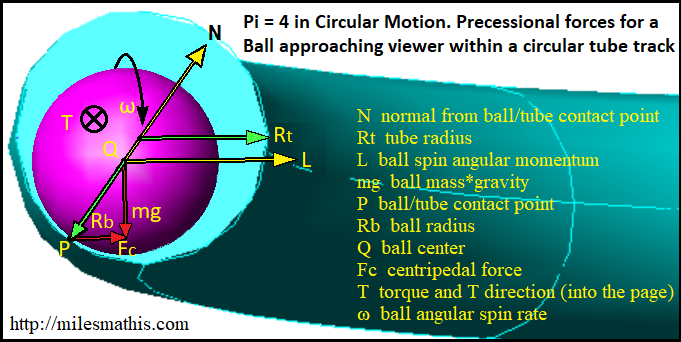
1. Added ω - the ball's angular spin rate.
2. Added Rt, the tube radius. Rt originates at the cross sectional center of the tube's small radius.
3. The normal N is now shown perpendicular to P and not directly (+ z) above P.
4. The centripetal force Fc now originates at the ball/tube contact point P.
Note, Fc and mg meet at a right angle.
.
Reporting some possible progress.
Happy belated Pi day, March 14, or is it the zeroth of April, the day before April fools day?
You might notice a change or two. My old machine died unexpectedly of a hard drive problem. The new machine is quite a bit different. Needless to say, it’s like starting all over again, my psyche may never recover.
Last time, I described Prof Lewin showing us how he uses both arms to torque a spinning bicycle wheel by its axle (that’s better spelling than last time) left or right like some kind of a steering wheel in order to turn the direction of the swivel seat he is sitting on. I said that’s how the ball in the circular tube track precesses. Well, Prof Lewin’s next precession demonstration uses the same spinning bicycle wheel suspended by a single point, applicable to the ball in the circular tube track. Suspend the spinning wheel by either the left or the right ends of the axle. The youtube image in my prior post shows a view of the spinning wheel along the axle, or spin axis, or L, or the direction of the spin angular momentum.
Here’s a slightly cleaned up blackboard diagram of the suspended spinning wheel Prof Lewin draws during the video.

Of course the spinning wheel as shown doesn’t flop over, as the wheel spins it will continually precess or orbit about the suspension point due to the constant force of gravity – increasing the weight increases the precession speed.

The large diagram above shows how I believe the ball in the circular tube track is effectively ‘suspended’ while traveling along the path balanced between centripetal and gravitational forces, up a bit on the tube’s outside wall. The spin axis is constantly chasing the torgue around the circular track. I’m still wondering whether the straight line between the ball/tube contact point, and the ball center is created by Fc and the mg vectors as shown is what creates the outside path or not.
P.S. After giving it some more thought, I’ve made a few changes to the previous diagram as shown below.

1. Added ω - the ball's angular spin rate.
2. Added Rt, the tube radius. Rt originates at the cross sectional center of the tube's small radius.
3. The normal N is now shown perpendicular to P and not directly (+ z) above P.
4. The centripetal force Fc now originates at the ball/tube contact point P.
Note, Fc and mg meet at a right angle.
.
Last edited by LongtimeAirman on Fri Mar 19, 2021 12:49 pm; edited 1 time in total (Reason for editing : added P.S. and latest precessional diagram)
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
Chromium6 likes this post
 Re: PI NINE - Pi experiment with two edge track
Re: PI NINE - Pi experiment with two edge track
.
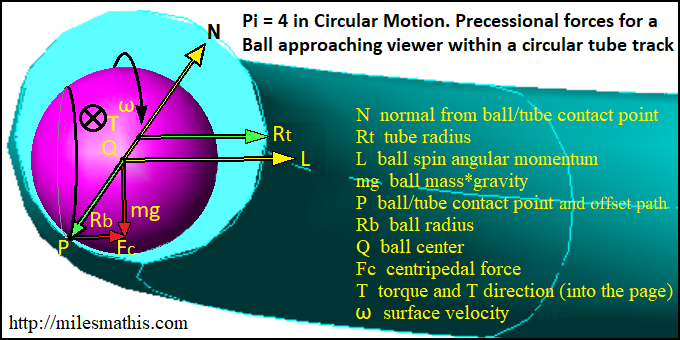
In case you’re wondering, I’m slowly identifying what I believe are all the pertinents necessary for properly describing the ball’s motion through the curved tube track. Small progress can take me forever, my apologies. Feel free to comment.
Changes made to the above image include:
1. Added a new ‘offset path’, a circular cross section passing through P, and added to the end of the P definition ‘and offset path’. As the ball rolls and precesses around the circular tube track, we can imagine the set of all ball/tube contact points make a single line circular path at some height up the tube’s outer wall. P also creates a rolling point contact path on the ball’s surface, a smaller rolling circumference not on the ball’s centerline spin equator. Like Miles and the engineer noted for the dual edge slot track.
2. After adding “ω ball angular spin rate” I realized I was thinking ω = 2πf in radians. I needed to correct that, by re-reading Miles’ Angular Velocity and Angular Momentum paper again*. I changed the ω definition to “surface velocity”, and I may change it again.
Given that paper, one simply cannot use all the current circular motion equations Professor Lewin uses in his lecture. Paraphrasing Miles, the false linear to angular equation v=rω, is used all over the place.
Airman. Hopefully more later.
*
http://milesmathis.com/index.html

In case you’re wondering, I’m slowly identifying what I believe are all the pertinents necessary for properly describing the ball’s motion through the curved tube track. Small progress can take me forever, my apologies. Feel free to comment.
Changes made to the above image include:
1. Added a new ‘offset path’, a circular cross section passing through P, and added to the end of the P definition ‘and offset path’. As the ball rolls and precesses around the circular tube track, we can imagine the set of all ball/tube contact points make a single line circular path at some height up the tube’s outer wall. P also creates a rolling point contact path on the ball’s surface, a smaller rolling circumference not on the ball’s centerline spin equator. Like Miles and the engineer noted for the dual edge slot track.
2. After adding “ω ball angular spin rate” I realized I was thinking ω = 2πf in radians. I needed to correct that, by re-reading Miles’ Angular Velocity and Angular Momentum paper again*. I changed the ω definition to “surface velocity”, and I may change it again.
Given that paper, one simply cannot use all the current circular motion equations Professor Lewin uses in his lecture. Paraphrasing Miles, the false linear to angular equation v=rω, is used all over the place.
Miles wrote.
The correction for all this is fairly simple, although it required me to study the Principia very closely. We need a new equation to go from tangential or linear velocity to orbital velocity, which I am calling ω. Newton does not give us that equation, and no one else has supplied it since then. We can find it by following Newton to his ultimate interval, which is the same as going to the limit. We use the Pythagorean Theorem. As t→0,
ω2 → v2 - Δv2
and, v2 + r2 = (Δv + r)2
So, by substitution, ω2 + Δv2 + r2 = Δv2 + 2Δvr + r2
Δv = √ v2 + r2) - r = ω2/2r
v = √[(ω4/4r2) + ω2]
ω = √[2r√v2 + r2) - 2r2]
r = √[ω4/(4v2 - 4ω2)]
Not as simple as the current equation, but much more logical. Instead of strange scaling, we get a logical progression. As r gets larger, the angular velocity approaches the tangential velocity. This is because with larger objects, the curve loses curvature, becoming more like the straight line. With smaller objects, the curvature increases, and the angular velocity may become a small fraction of the tangential velocity. And if v and ω diverge greatly, as with very small particles, this equation can be simplified to
v = ω/r
Yes, it is just the inverse of the current equation.
…
Of course I have changed the definition of ω above. It is now the angular velocity measured in meters and v is the tangential velocity measured in meters.
Airman. Hopefully more later.
*
http://milesmathis.com/index.html
.2. Angular Velocity and Angular Momentum. http://milesmathis.com/angle.html
Both current equations are shown to be false. 5pp.
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
Chromium6 likes this post
 Re: PI NINE - Pi experiment with two edge track
Re: PI NINE - Pi experiment with two edge track
.
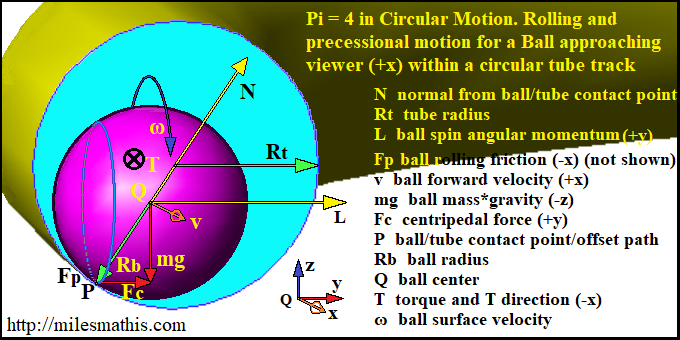
Precession of a Rolling ball in a curved tube. The view is now slightly downward. The ball’s forward (linear) velocity v is in the +x direction, pointed roughly at the viewer’s right arm. It identifies a rolling friction at point P, has improved points, an axis reference and vector directions in the variable descriptions.
The image shows a cross section of the circular tube track passing through the center of the ball (Q) and perpendicular to the ball’s forward direction v. The x,y,z reference axis applies to the moving ball anywhere in the circular track, the frame of reference rotates around the track always keeping the front of the rolling ball in view. v is always straight ahead (+x) and the ball spin axis angular momentum L is always pointed to the ball’s left (the viewer’s right) toward the circular tube track center (+y), meaning the ball is always rolling forward without tilting. The ball/tube contact path appears as a single point P.
That side contact point may come as a surprise to some. I suppose most of us assume that no matter how high or low on the tube’s outside wall the rolling ball’s contact point is, that point can still lie on the rolling ball’s spin equator. For example, rolling sideways round the inside of the tube, in which case, the ball’s spin angular momentum (L) would be almost vertical (+/-z). Ok, that seems like it would work mechanically. Wouldn’t the ball exiting the curved tube spin like a top? I didn’t notice that in Steven’s experiment. I don’t see how the ball/curved tube/gravity interaction could turn the ball’s initial straight section rolling spin axis of L=+y to L=+z inside the curved tube. On the other hand, the precession answer I’ve diagrammed several times and am now trying to describe makes good sense to me.
When the ball is traveling along a circular contact path at some height up the curving tube’s outside wall, the ball cannot flop over point P toward the bottom of the tube because the rolling ball has spin angular momentum and must behave gyroscopically. Sure, there’s a slight downward tilt to the ball’s spin axis under the force of gravity, just as when professor Lewin used the spinning wheel he held in front of him to constantly turn the direction of the swivel seat he was sitting on left or right by rotating his 9 and 3 o’clock axle end hand positions to either 8 and 2, or 10 and 4. While greatly exerting himself saying something like “you can feel the force!” L is essentially pointed to the circular track center, although slightly down the track center’s z dimension due to this slight tilt. The faster the spin, the less the tilt. As the spinning slows the tilt increases. As such, the ball’s rotation about the circular track is not due to the slight downward tilt.
The force of gravity that would flop over a non-spinning object is converted by the ball’s angular motion into a (-x) torque that turns the ball’s spin angular momentum L not downward, but towards the direction of the torque, ninety degrees to the rear. The ball's spin axis turns left in the horizontal plane. Precession.
The “rolling ball in the curved tube supported at P” image closely resembles the precession diagram of a spinning wheel supported at either left or right ends of the axle. A spinning gyroscopic rotor or bicycle wheel supported at left or right axle ends precesses, so does the ball in the circular tube track and for the same reason, the constant pull of gravity. The ball moving along a contact line path in a curved tube supported somewhere on the side of the rolling ball’s spherical surface (P) seems a lot more complicated than simply supporting a spinning rotor or wheel by its left or right axle end. I'm still trying to figure it out.
The ball starts rolling with an acceleration ramp, then goes through a straight section to measure its linear velocity. In that straight section, because of gravity, the bottom of the rolling ball is making a good rolling contact with the bottom of the straight tube track. Each rotation of the ball equals another ball circumference distance traveled.
The rolling ball entering the curved section will try to maintain both its linear and angular momentum. The outside curved tube wall encroaching in front of the ball will cause the ball/tube contact path to move off and away from the bottom of the tube and the bottom of the ball. Contact point P will quickly climb up the wall, converting some linear momentum to angular momentum, slowing the ball's spin rate while increasing P's radial distance from the ball’s center of gravity. Increasing the gravitational force torque strength, increasing the ball’s precession rate until it matches the tube’s curvature, where centripetal and gravity forces balance. Or something like that.
Maybe I can work up some numbers next.
Thanks Cr6.
.

Precession of a Rolling ball in a curved tube. The view is now slightly downward. The ball’s forward (linear) velocity v is in the +x direction, pointed roughly at the viewer’s right arm. It identifies a rolling friction at point P, has improved points, an axis reference and vector directions in the variable descriptions.
The image shows a cross section of the circular tube track passing through the center of the ball (Q) and perpendicular to the ball’s forward direction v. The x,y,z reference axis applies to the moving ball anywhere in the circular track, the frame of reference rotates around the track always keeping the front of the rolling ball in view. v is always straight ahead (+x) and the ball spin axis angular momentum L is always pointed to the ball’s left (the viewer’s right) toward the circular tube track center (+y), meaning the ball is always rolling forward without tilting. The ball/tube contact path appears as a single point P.
That side contact point may come as a surprise to some. I suppose most of us assume that no matter how high or low on the tube’s outside wall the rolling ball’s contact point is, that point can still lie on the rolling ball’s spin equator. For example, rolling sideways round the inside of the tube, in which case, the ball’s spin angular momentum (L) would be almost vertical (+/-z). Ok, that seems like it would work mechanically. Wouldn’t the ball exiting the curved tube spin like a top? I didn’t notice that in Steven’s experiment. I don’t see how the ball/curved tube/gravity interaction could turn the ball’s initial straight section rolling spin axis of L=+y to L=+z inside the curved tube. On the other hand, the precession answer I’ve diagrammed several times and am now trying to describe makes good sense to me.
When the ball is traveling along a circular contact path at some height up the curving tube’s outside wall, the ball cannot flop over point P toward the bottom of the tube because the rolling ball has spin angular momentum and must behave gyroscopically. Sure, there’s a slight downward tilt to the ball’s spin axis under the force of gravity, just as when professor Lewin used the spinning wheel he held in front of him to constantly turn the direction of the swivel seat he was sitting on left or right by rotating his 9 and 3 o’clock axle end hand positions to either 8 and 2, or 10 and 4. While greatly exerting himself saying something like “you can feel the force!” L is essentially pointed to the circular track center, although slightly down the track center’s z dimension due to this slight tilt. The faster the spin, the less the tilt. As the spinning slows the tilt increases. As such, the ball’s rotation about the circular track is not due to the slight downward tilt.
The force of gravity that would flop over a non-spinning object is converted by the ball’s angular motion into a (-x) torque that turns the ball’s spin angular momentum L not downward, but towards the direction of the torque, ninety degrees to the rear. The ball's spin axis turns left in the horizontal plane. Precession.
The “rolling ball in the curved tube supported at P” image closely resembles the precession diagram of a spinning wheel supported at either left or right ends of the axle. A spinning gyroscopic rotor or bicycle wheel supported at left or right axle ends precesses, so does the ball in the circular tube track and for the same reason, the constant pull of gravity. The ball moving along a contact line path in a curved tube supported somewhere on the side of the rolling ball’s spherical surface (P) seems a lot more complicated than simply supporting a spinning rotor or wheel by its left or right axle end. I'm still trying to figure it out.
The ball starts rolling with an acceleration ramp, then goes through a straight section to measure its linear velocity. In that straight section, because of gravity, the bottom of the rolling ball is making a good rolling contact with the bottom of the straight tube track. Each rotation of the ball equals another ball circumference distance traveled.
The rolling ball entering the curved section will try to maintain both its linear and angular momentum. The outside curved tube wall encroaching in front of the ball will cause the ball/tube contact path to move off and away from the bottom of the tube and the bottom of the ball. Contact point P will quickly climb up the wall, converting some linear momentum to angular momentum, slowing the ball's spin rate while increasing P's radial distance from the ball’s center of gravity. Increasing the gravitational force torque strength, increasing the ball’s precession rate until it matches the tube’s curvature, where centripetal and gravity forces balance. Or something like that.
Maybe I can work up some numbers next.
Thanks Cr6.
.
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
Chromium6 likes this post
 Re: PI NINE - Pi experiment with two edge track
Re: PI NINE - Pi experiment with two edge track
.

A. A rolling ball accelerates down a tube ramp. B. Viewing the ball rolling at a constant velocity to the right through straight tube. C. Viewing the ball (perpendicularly) rolling to the right through curved tube. D. Head-on view of the ball in the curve tube. And E. Head-on view of the ball rolling in the straight tube. I'll share if I make any significant changes. I suppose another panel needs to be added between B and C - “Entering the curve”. Prof Lewin’s spinning wheel diagrams convinced me the ball in the Pi=4 tube track precesses. Copying his diagrams for the tubes been a good way to help focus my thoughts. I should correct a few of my most recent comments.
The force of gravity causes both the slight downward tilt and precession. The slight tilt shows that the downward force of gravity is present, and how it is effecting the spin. Starting with a very high velocity spin at 90 degrees as with a spinning top, there would almost no tilt to the spinning object. With wheels and rotors suspended by a single axle end, when the slight tilt is present, we see the tilt rotates about the spinning object’s point of contact point at a rate – the precession rate. As that spinning object loses energy and slows, the tilt slowly grows.
The ball in the curved tube track appears subject a precession constraint. The only slight downward tilt direction available to the ball rolling on the curved tube’s outside wall is toward the circular track center. The precession rate of the ball around the center of the curved tube track should equal the ball’s position in the circular tube track. Given its forward velocity, the ball’s precession rate must agree with the track curvature.
This sentence requires much more thought and some correction. “Slowing the ball’s spin rate” is wrong, the ball maintains its spin rate. Instead, by rolling on its edge, somewhere up the side wall, the ball is moving forward with a reduced rotation rolling distance; therefore a slower velocity compared to a ball rolling on its spin equator in the straight tube. Similar to Miles pointing out the ball in the slotted track can never travel as fast as the ball in Steven’s track.
Another thing, "increasing P's radial distance from the ball’s center of gravity" is confusing. Radial here is measured from the center of the track, or the y axis difference between the ball’s center of gravity Q(x,y,z), and the contact point P(x,y,z) y coordinates.
Refer to diagram A. According to professor Lewin, L = rmv= Iω, the acceleration, a of the circular mass rolling down the ramp is given by,
a = (MR^2gsinβ) / (MR^2+IQ)
Miles explains how L = rmv= Iω. it is false in his Angular Velocity and Angular Momentum paper *.
There’s a problem here. The circle can be either solid or hollow, cylindrical or spherical. Plugging in the I values for the different spinning masses we see more to I than just MR^2.
Solid cylinder: I=(1/2)MR^2, and a = (2/3)gsinβ in (m/s^2)
Hollow cylinder: I=MR^2, and a = (½)gsinβ
Solid sphere: I=(2/5)MR^2, and a = (5/7)gsinβ
Thin spherical shell: I=(2/3)MR^2, and a = (3/5)gsinβ
Regardless of mass, length or radius. Solid spheres accelerate the fastest.
Apparently not all spinning masses are equal. All well and good, when talking about angular momentum, we can do without I’s M^2R component. There still needs to be some way to differentiate between the various mass distributions. Can we keep I as a fractional coefficient?
I'm doing my best trying to understand ω.
Your patience is appreciated.
Professor Lewin's Rolling Motion, Gyroscopes, VERY NON-INTUITIVE.
https://www.youtube.com/watch?v=XPUuF_dECVI
*
http://milesmathis.com/index.html
Angular Velocity and Angular Momentum. http://milesmathis.com/angle.html
Both current equations are shown to be false. 5pp
.

A. A rolling ball accelerates down a tube ramp. B. Viewing the ball rolling at a constant velocity to the right through straight tube. C. Viewing the ball (perpendicularly) rolling to the right through curved tube. D. Head-on view of the ball in the curve tube. And E. Head-on view of the ball rolling in the straight tube. I'll share if I make any significant changes. I suppose another panel needs to be added between B and C - “Entering the curve”. Prof Lewin’s spinning wheel diagrams convinced me the ball in the Pi=4 tube track precesses. Copying his diagrams for the tubes been a good way to help focus my thoughts. I should correct a few of my most recent comments.
Airman wrote. As such, the ball’s rotation about the circular track is not due to the slight downward tilt.
The force of gravity causes both the slight downward tilt and precession. The slight tilt shows that the downward force of gravity is present, and how it is effecting the spin. Starting with a very high velocity spin at 90 degrees as with a spinning top, there would almost no tilt to the spinning object. With wheels and rotors suspended by a single axle end, when the slight tilt is present, we see the tilt rotates about the spinning object’s point of contact point at a rate – the precession rate. As that spinning object loses energy and slows, the tilt slowly grows.
The ball in the curved tube track appears subject a precession constraint. The only slight downward tilt direction available to the ball rolling on the curved tube’s outside wall is toward the circular track center. The precession rate of the ball around the center of the curved tube track should equal the ball’s position in the circular tube track. Given its forward velocity, the ball’s precession rate must agree with the track curvature.
Airman wrote. Contact point P will quickly climb up the wall, converting some linear momentum to angular momentum, slowing the ball's spin rate while increasing P's radial distance from the ball’s center of gravity.
This sentence requires much more thought and some correction. “Slowing the ball’s spin rate” is wrong, the ball maintains its spin rate. Instead, by rolling on its edge, somewhere up the side wall, the ball is moving forward with a reduced rotation rolling distance; therefore a slower velocity compared to a ball rolling on its spin equator in the straight tube. Similar to Miles pointing out the ball in the slotted track can never travel as fast as the ball in Steven’s track.
Another thing, "increasing P's radial distance from the ball’s center of gravity" is confusing. Radial here is measured from the center of the track, or the y axis difference between the ball’s center of gravity Q(x,y,z), and the contact point P(x,y,z) y coordinates.
Refer to diagram A. According to professor Lewin, L = rmv= Iω, the acceleration, a of the circular mass rolling down the ramp is given by,
a = (MR^2gsinβ) / (MR^2+IQ)
Miles explains how L = rmv= Iω. it is false in his Angular Velocity and Angular Momentum paper *.
Miles Wrote. This means that the whole moment of inertia idea was just a fudge, used to make v = rω. Historically, mathematicians started with Newton's equations, mainly v = 2πr/t, which they wanted to keep. To keep it, they had to fudge these angular equations. In order to maintain the equation v = rω, the moment of inertia was created. But using my simple corrections, we see that the angular momentum is not L = mvr = Iω. The angular momentum equation is just L = mω. We didn't need a moment of inertia, we just needed to correct the earlier equations of Newton, which were wrong.
There’s a problem here. The circle can be either solid or hollow, cylindrical or spherical. Plugging in the I values for the different spinning masses we see more to I than just MR^2.
Solid cylinder: I=(1/2)MR^2, and a = (2/3)gsinβ in (m/s^2)
Hollow cylinder: I=MR^2, and a = (½)gsinβ
Solid sphere: I=(2/5)MR^2, and a = (5/7)gsinβ
Thin spherical shell: I=(2/3)MR^2, and a = (3/5)gsinβ
Regardless of mass, length or radius. Solid spheres accelerate the fastest.
Apparently not all spinning masses are equal. All well and good, when talking about angular momentum, we can do without I’s M^2R component. There still needs to be some way to differentiate between the various mass distributions. Can we keep I as a fractional coefficient?
I'm doing my best trying to understand ω.
Your patience is appreciated.
Professor Lewin's Rolling Motion, Gyroscopes, VERY NON-INTUITIVE.
https://www.youtube.com/watch?v=XPUuF_dECVI
*
http://milesmathis.com/index.html
Angular Velocity and Angular Momentum. http://milesmathis.com/angle.html
Both current equations are shown to be false. 5pp
.
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
 Re: PI NINE - Pi experiment with two edge track
Re: PI NINE - Pi experiment with two edge track
.

The diagram includes several changes since last week. There aren’t many additions to my comments below, still, the more I think about it, the better I like this precession idea.
Given Steven Oostijk’s experiment confirming Pi=4, Pi=4 for curved motion. One might ask, what exactly is the curved motion? A ball rolling on a flat surface or in a straight tube has a single spin angular momentum axis (L) vector direction which does not constitute curved motion. The circular track constrains a rolling ball with linear velocity v to a circular path at a track radius about the track center. I believe that the ball rolling in the circular tube track rotates about the circular track center through gravitational precession.
Very similar to the well known gyroscopic precession example – the single axle end supported spinning bicycle wheel professor Lewin demonstrated. The spinning wheel constantly rotates its spin angular momentum axis L around the hanging cable/axle end support point. The precession rotation is caused by the rotor’s own weight directed downward through the rotor’s center of mass, at some horizontal separation distance (P(y)-Q(y)) from the axle end/suspension point. The downward force at that horizontal separation creates a torque (+/-x) that constantly turns the rotor’s spin angular momentum axis L toward the direction of the torque in the horizontal plane. The single stationary contact point in the precession example is very similar – inversely – to the contact point path the ball makes when traveling through the circular tube track.
Here are the numbers from Steven’s experiment 1,
https://www.youtube.com/watch?v=QhuvUSS3KAE
ball: mass m=2.1g, radius R=0.004m, and initial linear velocity v=1.2 m/s.
tube: Outside diameter = 16mm, inside diameter Id=12mm.
Circular track: Inner diameter = 16cm, centerline circular track diameter = 17.6cm.
Straight track: Length, 70.4cm (4x17.6).
Two Steven quotes from the comments section.
Both balls start at ~1.2m/s and end at ~1.0m/s.
Several velocities were used with no variation in the result. Certain minimum velocity has to be used to overcome static friction.
I didn’t see an initial velocity for the larger experiment 2.
Panel A. The acceleration ramp. A straight tube downward incline. The top is 15cm high, I don’t know the length of the ramp or the ramp’s angle. N is the normal, perpendicular at the ball/tube contact point P(x,y,z). Q(x,y,z) is the center of the circular object, with mass M and radius R, through which the downward force of gravity - Mg, ball mass (2.1 g)* gravity (9.81 m/s), is felt. Mg is decomposed into two forces, normal to the surface (therefore providing no acceleration to the ball) and in the forward direction. μ is the coefficient of friction and FF is the frictional force. The angular velocity ωt, linear velocity vt and spin angular momentum Lt are increasing with time on the ramp, due to the downward force of gravity. Per mainstream theory, Prof Lewin shows that the acceleration (a) of the circular mass M with radius R is:
a = (MR^2gsinβ) / (MR^2+IQ). For a solid sphere: IQ=(2/5)MR^2, and a = (5/7)gsinβ.
The acceleration (a) is probably corrupted by mainstream’s false equivalency v = ωR. Miles has redefined ω from orbital velocity in rads/sec to an angular velocity in meters/sec. I mentioned last time that of all the circular type masses, hollow or solid, cylindrical or sphere, spheres accelerate the fastest. Miles says we can do without the moment of inertia I, but we still need to differentiate between difference mass configurations. Miles has redefined mass in terms of density and volume, perhaps specific mass/volume densities can be defined as well.
Panel B. The straight tube. One c-track diameter length straight section intended to compare tracks and determine the balls’ initial velocity. The diagram also applies along the straight track’s four diameter length. The side view (+y) shows the straight track ball rolling from left to right (+x). The linear velocity, VQ=1.2 m/s. Each ball’s straight rolling rotation advances the ball 2πR to the right. The ball/tube contact point lies at the bottom of the ball’s spin axis equator and bottom of the tube, as shown in panel E. The ball’s circumference is just over 25 millimeters, the ball in the straight tube track will make 28 rolls in the 0.64 seconds (including the ball slow down) to complete the track. I assume there’s good rolling contact between the metal ball and pvc plastic tube, which I believe is another stroke of good fortune in Steven’s experiment, not just in the straight, but also in the circular track.
First, what is ω, the ball’s rolling angular velocity? I guess we go to the source, Miles’ linear velocity v, angular velocity ω and radius r equalities, good for any size r, from the smallest photon radius to the astronomical.
v = √[(ω4/4r2) + ω2]
ω = √[2r√v2 + r2) - 2r2]
r = √[ω4/(4v2 - 4ω2)]
The initial linear velocity v=1.2 m/s, r=0.004 m.
ω = √[2(0.004)√1.2^2 + (0.004)^2) - 2(0.004)^2]
ω = 0.09781 m/s. I’m trying to get some sense of scale, at the 8mm diameter ball bearing size there’s a large difference between the linear and angular velocities 1.2 m/s and 0.0978 m/s.
Next, the ball’s straight track spin angular momentum,
L = mω.
L = 2.1*0.09781
L = 0.2054 gm/s in the +y direction
Panel C. in the curved tube, side view, and Panel D in the curve, looking back.
I tried creating another diagram showing how the ball behaves when it enters the curved tube but realised one may best understand the transition to the curve by comparing panels D and E, looking back at the both the curved and straight sections. The ball will continue rolling forward, maintaining it’s horizontal spin axis as the ball/tube contact point rolls up and away from the bottom of the tube and bottom of the ball. The ball ends up rolling about on a lateral circular section I call an offset path. The ball on the offset path travels at a lower velocity than the ball in the straight section.
In panel D, the ball’s precession in the curved tube results from the fact that the ball/tube contact point P is somewhere up the tube’s outside wall and the balls outside lateral surface, horizontally separated (P(y)-Q(y)) from the ball’s center of gravity. The ball in panel D is shown tilted slightly toward the center of the tube (or track center) indicating the presence of the gravitational force. The downward force applied at the horizontal separation from the point of contact causes a torque, tau or τ in the negative x direction. That causes the spin angular momentum axis L to chase the torque, turning in the horizontal plane.
τ = R·F sin Ɵ = (P(y)-Q(y))·Mg sin 90
τ = (P(y)-Q(y))·Mg mg/s in the (-x) direction.
Tau and L maintain their 90 degree relationship as the rolling ball rotates about the circular track center.
The ball will continue to climb the wall with an almost horizontal spin axis, increasing the (P(y)-Q(y)) separation distance and so increasing the torque’s strength, causing the precession rate to increase till the ball’s gravity and centripetal forces balance, and the ball’s precession matches the track curvature.
According to one reference I found, the precession rate for the spinning wheel is found by
the precession angular speed ωp,
ωp=mgr/L
That’s not right because it’s mainstream ω in radians/sec. I believe the ball’s precession rate should be equal to the ball’s track velocity.
The initial linear velocity v=1.2 m/s. The radius for the circular track is 17.6cm/2 = 8.8cm
ωp = √[2r√v2 + r2) - 2r2]
ωp = √[2(0.088)√1.2^2 + (0.088)^2) - 2(0.088)^2]
ωp = 0.4430 m/s.
I don’t know if that’s right or wrong. It is smaller than the linear velocity.
Then the spin angular momentum of the ball’s motion around the circular track must be
L = mω.
L = 2.1*0.4430 m/s.
L = 0.9304 gm/s in the +z direction
These numbers haven't helped me much. Anyway, that’s where I’m at. I'll stop posting to this thread unless there’s discussion or I make significant changes.
P.S. P(y)-Q(y) is occurring in the horizontal plane, not in the vertical. Changed vertical separations to horizontal separations. Also made a few more cleanup changes to the diagram and replaced it.
.

The diagram includes several changes since last week. There aren’t many additions to my comments below, still, the more I think about it, the better I like this precession idea.
Given Steven Oostijk’s experiment confirming Pi=4, Pi=4 for curved motion. One might ask, what exactly is the curved motion? A ball rolling on a flat surface or in a straight tube has a single spin angular momentum axis (L) vector direction which does not constitute curved motion. The circular track constrains a rolling ball with linear velocity v to a circular path at a track radius about the track center. I believe that the ball rolling in the circular tube track rotates about the circular track center through gravitational precession.
Very similar to the well known gyroscopic precession example – the single axle end supported spinning bicycle wheel professor Lewin demonstrated. The spinning wheel constantly rotates its spin angular momentum axis L around the hanging cable/axle end support point. The precession rotation is caused by the rotor’s own weight directed downward through the rotor’s center of mass, at some horizontal separation distance (P(y)-Q(y)) from the axle end/suspension point. The downward force at that horizontal separation creates a torque (+/-x) that constantly turns the rotor’s spin angular momentum axis L toward the direction of the torque in the horizontal plane. The single stationary contact point in the precession example is very similar – inversely – to the contact point path the ball makes when traveling through the circular tube track.
Here are the numbers from Steven’s experiment 1,
https://www.youtube.com/watch?v=QhuvUSS3KAE
ball: mass m=2.1g, radius R=0.004m, and initial linear velocity v=1.2 m/s.
tube: Outside diameter = 16mm, inside diameter Id=12mm.
Circular track: Inner diameter = 16cm, centerline circular track diameter = 17.6cm.
Straight track: Length, 70.4cm (4x17.6).
Two Steven quotes from the comments section.
Both balls start at ~1.2m/s and end at ~1.0m/s.
Several velocities were used with no variation in the result. Certain minimum velocity has to be used to overcome static friction.
I didn’t see an initial velocity for the larger experiment 2.
Panel A. The acceleration ramp. A straight tube downward incline. The top is 15cm high, I don’t know the length of the ramp or the ramp’s angle. N is the normal, perpendicular at the ball/tube contact point P(x,y,z). Q(x,y,z) is the center of the circular object, with mass M and radius R, through which the downward force of gravity - Mg, ball mass (2.1 g)* gravity (9.81 m/s), is felt. Mg is decomposed into two forces, normal to the surface (therefore providing no acceleration to the ball) and in the forward direction. μ is the coefficient of friction and FF is the frictional force. The angular velocity ωt, linear velocity vt and spin angular momentum Lt are increasing with time on the ramp, due to the downward force of gravity. Per mainstream theory, Prof Lewin shows that the acceleration (a) of the circular mass M with radius R is:
a = (MR^2gsinβ) / (MR^2+IQ). For a solid sphere: IQ=(2/5)MR^2, and a = (5/7)gsinβ.
The acceleration (a) is probably corrupted by mainstream’s false equivalency v = ωR. Miles has redefined ω from orbital velocity in rads/sec to an angular velocity in meters/sec. I mentioned last time that of all the circular type masses, hollow or solid, cylindrical or sphere, spheres accelerate the fastest. Miles says we can do without the moment of inertia I, but we still need to differentiate between difference mass configurations. Miles has redefined mass in terms of density and volume, perhaps specific mass/volume densities can be defined as well.
Panel B. The straight tube. One c-track diameter length straight section intended to compare tracks and determine the balls’ initial velocity. The diagram also applies along the straight track’s four diameter length. The side view (+y) shows the straight track ball rolling from left to right (+x). The linear velocity, VQ=1.2 m/s. Each ball’s straight rolling rotation advances the ball 2πR to the right. The ball/tube contact point lies at the bottom of the ball’s spin axis equator and bottom of the tube, as shown in panel E. The ball’s circumference is just over 25 millimeters, the ball in the straight tube track will make 28 rolls in the 0.64 seconds (including the ball slow down) to complete the track. I assume there’s good rolling contact between the metal ball and pvc plastic tube, which I believe is another stroke of good fortune in Steven’s experiment, not just in the straight, but also in the circular track.
First, what is ω, the ball’s rolling angular velocity? I guess we go to the source, Miles’ linear velocity v, angular velocity ω and radius r equalities, good for any size r, from the smallest photon radius to the astronomical.
v = √[(ω4/4r2) + ω2]
ω = √[2r√v2 + r2) - 2r2]
r = √[ω4/(4v2 - 4ω2)]
The initial linear velocity v=1.2 m/s, r=0.004 m.
ω = √[2(0.004)√1.2^2 + (0.004)^2) - 2(0.004)^2]
ω = 0.09781 m/s. I’m trying to get some sense of scale, at the 8mm diameter ball bearing size there’s a large difference between the linear and angular velocities 1.2 m/s and 0.0978 m/s.
Next, the ball’s straight track spin angular momentum,
L = mω.
L = 2.1*0.09781
L = 0.2054 gm/s in the +y direction
Panel C. in the curved tube, side view, and Panel D in the curve, looking back.
I tried creating another diagram showing how the ball behaves when it enters the curved tube but realised one may best understand the transition to the curve by comparing panels D and E, looking back at the both the curved and straight sections. The ball will continue rolling forward, maintaining it’s horizontal spin axis as the ball/tube contact point rolls up and away from the bottom of the tube and bottom of the ball. The ball ends up rolling about on a lateral circular section I call an offset path. The ball on the offset path travels at a lower velocity than the ball in the straight section.
In panel D, the ball’s precession in the curved tube results from the fact that the ball/tube contact point P is somewhere up the tube’s outside wall and the balls outside lateral surface, horizontally separated (P(y)-Q(y)) from the ball’s center of gravity. The ball in panel D is shown tilted slightly toward the center of the tube (or track center) indicating the presence of the gravitational force. The downward force applied at the horizontal separation from the point of contact causes a torque, tau or τ in the negative x direction. That causes the spin angular momentum axis L to chase the torque, turning in the horizontal plane.
τ = R·F sin Ɵ = (P(y)-Q(y))·Mg sin 90
τ = (P(y)-Q(y))·Mg mg/s in the (-x) direction.
Tau and L maintain their 90 degree relationship as the rolling ball rotates about the circular track center.
The ball will continue to climb the wall with an almost horizontal spin axis, increasing the (P(y)-Q(y)) separation distance and so increasing the torque’s strength, causing the precession rate to increase till the ball’s gravity and centripetal forces balance, and the ball’s precession matches the track curvature.
According to one reference I found, the precession rate for the spinning wheel is found by
the precession angular speed ωp,
ωp=mgr/L
That’s not right because it’s mainstream ω in radians/sec. I believe the ball’s precession rate should be equal to the ball’s track velocity.
The initial linear velocity v=1.2 m/s. The radius for the circular track is 17.6cm/2 = 8.8cm
ωp = √[2r√v2 + r2) - 2r2]
ωp = √[2(0.088)√1.2^2 + (0.088)^2) - 2(0.088)^2]
ωp = 0.4430 m/s.
I don’t know if that’s right or wrong. It is smaller than the linear velocity.
Then the spin angular momentum of the ball’s motion around the circular track must be
L = mω.
L = 2.1*0.4430 m/s.
L = 0.9304 gm/s in the +z direction
These numbers haven't helped me much. Anyway, that’s where I’m at. I'll stop posting to this thread unless there’s discussion or I make significant changes.
P.S. P(y)-Q(y) is occurring in the horizontal plane, not in the vertical. Changed vertical separations to horizontal separations. Also made a few more cleanup changes to the diagram and replaced it.
.
Last edited by LongtimeAirman on Wed Apr 14, 2021 10:51 pm; edited 2 times in total (Reason for editing : added P.S. and replaced the diagram twice)
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
Chromium6 likes this post
 Re: PI NINE - Pi experiment with two edge track
Re: PI NINE - Pi experiment with two edge track
Something clicked recently for me.
I'm in the camp of opinion that the ball in the curved tubular track is moving in a very complicated way.
THe ball has velocity as it enters the curve, it also has angular momentum due to rolling and its mass. It will also have translational momentum, but I have trouble imagining that. The complication I see is the initial changing of the axis of its rolling. When it hits the first part of the curve it will ride up the outside wall of the track. At this point I have only a sketch of what happens. I imagine it will ride up HIGHER on the outside wall at this initial period, than it will at any other time during its travel around the curved tube.
As it goes up the track it will be losing energy due to working against gravity, it will at sometime experience more friction against the wall than a ball rolling the straight track. That friction will cause the axis of rotation a torque, but it will not be acting on the axis but on the rolling part. This will cause sliding of the ball against the track perhaps. procession is not really part of this, this is something else.
So when the ball rides up the wall and has its angular momentum torqued, there will be resistance to the the change in angular momentum axis. This will be removing energy from the ball.
So we have gravity, friction, and change in the axis of angular momentum.
But there is more, the point of contact of the ball cannot be a circle as the curved track is circular. It will be a squiggle that oscillates. It will ride high up the outer wall initially, where a point of contact with the ball ends up being highest during the whole experiment, then that point of contact will fall, due to gravity. It will roll in the circle at some point at the bottom of the tube, but I think it will then roll up the inner wall, perhaps only a tiny amount. At some point during this process it will settle down its oscillation, the squiggle that is traced by its point of contact will get less squiggly. During this process, friction and changes in the axis of rotation and thus torque on the angular momentum axis is beyond what I can fully imagine. It seems really complicated.
The ball will never "settle" down to a circle but will always have a little squiggle perhaps.
Lastly, when it first rides up the outer wall of the tube, it will exert a force against the wall of the tube, since the tube is not rigid, its ability to deform will drain energy from the ball and convert it to heat, also it may apply a force to the table, so that not only deformation will drain energy from the ball.
These factors explain for me why the curved tube will always slow the ball down, its a much more complicated form of movement than the straight tube.
I remember on Steven's video someone mentioned it would be cool to see the experiment done without the ball rolling, and I agree. All I can imagine is a ball made of ice or a cylinder of ice in a tube of ice perhaps. It may be possible to push the cylinder with air pressure and eliminate gravity in the experiment, and rolling, but I can't say. I think it would be different than either the rolling ball in a tube or on a milled two rail track.
I'm in the camp of opinion that the ball in the curved tubular track is moving in a very complicated way.
THe ball has velocity as it enters the curve, it also has angular momentum due to rolling and its mass. It will also have translational momentum, but I have trouble imagining that. The complication I see is the initial changing of the axis of its rolling. When it hits the first part of the curve it will ride up the outside wall of the track. At this point I have only a sketch of what happens. I imagine it will ride up HIGHER on the outside wall at this initial period, than it will at any other time during its travel around the curved tube.
As it goes up the track it will be losing energy due to working against gravity, it will at sometime experience more friction against the wall than a ball rolling the straight track. That friction will cause the axis of rotation a torque, but it will not be acting on the axis but on the rolling part. This will cause sliding of the ball against the track perhaps. procession is not really part of this, this is something else.
So when the ball rides up the wall and has its angular momentum torqued, there will be resistance to the the change in angular momentum axis. This will be removing energy from the ball.
So we have gravity, friction, and change in the axis of angular momentum.
But there is more, the point of contact of the ball cannot be a circle as the curved track is circular. It will be a squiggle that oscillates. It will ride high up the outer wall initially, where a point of contact with the ball ends up being highest during the whole experiment, then that point of contact will fall, due to gravity. It will roll in the circle at some point at the bottom of the tube, but I think it will then roll up the inner wall, perhaps only a tiny amount. At some point during this process it will settle down its oscillation, the squiggle that is traced by its point of contact will get less squiggly. During this process, friction and changes in the axis of rotation and thus torque on the angular momentum axis is beyond what I can fully imagine. It seems really complicated.
The ball will never "settle" down to a circle but will always have a little squiggle perhaps.
Lastly, when it first rides up the outer wall of the tube, it will exert a force against the wall of the tube, since the tube is not rigid, its ability to deform will drain energy from the ball and convert it to heat, also it may apply a force to the table, so that not only deformation will drain energy from the ball.
These factors explain for me why the curved tube will always slow the ball down, its a much more complicated form of movement than the straight tube.
I remember on Steven's video someone mentioned it would be cool to see the experiment done without the ball rolling, and I agree. All I can imagine is a ball made of ice or a cylinder of ice in a tube of ice perhaps. It may be possible to push the cylinder with air pressure and eliminate gravity in the experiment, and rolling, but I can't say. I think it would be different than either the rolling ball in a tube or on a milled two rail track.
3rd doorman- Posts : 25
Join date : 2020-04-03
Chromium6 likes this post
 Re: PI NINE - Pi experiment with two edge track
Re: PI NINE - Pi experiment with two edge track
Good ideas there 3rd doorman. It would be kind of cool to shrink down to a round circle-lattice of 16 photons and incrementally add "rings" to a "ball" and try it maybe. Then move up to adding several "atoms" of iron rings until something is created like a nano-ball that could be measured. But what is the ruler for measurement as it rolls in a "circle" ?
Chromium6- Posts : 818
Join date : 2019-11-29
 Re: PI NINE - Pi experiment with two edge track
Re: PI NINE - Pi experiment with two edge track
Thank you for the compliment. Unfortunately I can't visualize your cicle-lattice  . Also I don't know what you mean by adding rings to a ball. Doing an experiment at the nano level is way beyond my abilities, I have trouble visualizing how it would all be measured, indeed. I just usually assume I cannot work on photons because the equipment is beyond my means, financial but also intellectually they are very mysterious still.
. Also I don't know what you mean by adding rings to a ball. Doing an experiment at the nano level is way beyond my abilities, I have trouble visualizing how it would all be measured, indeed. I just usually assume I cannot work on photons because the equipment is beyond my means, financial but also intellectually they are very mysterious still.
Video and Balls on tracks is more approachable.
To answer your question, I believe that the ball should be in tracks of equal length as drawn with pi=3.14xxx. And that we should try and eliminate all kinds of energy loss, if its a significant energy loss, and see where the balls move compared to a grid embedded into the tracks. The grid for Steven was the markings at each quarter of circumfrence. The data would be video, from above if possible and everything should be high frame rate and in focus, but that is a wishlist only.
From there I would analyze by where the ball passed markers and what the time was and compare the travel of the two balls. Beyond that all I have is no money for equipment, no time, and ice! Maybe I can join the club, but I have no video camera and no editing station [sigh] its just a dream. I didn't know as much as airman about precession and I will have to keep reviewing his nice diagrams. The math still eludes me but I cannot study it intensively and just kind of feel the frustration that I'm still on the fence if pi=4 or if there is something else going on. I don't know, it looks like the math is failing, but even that is a matter of interpreting experiment, I find that difficult.
Video and Balls on tracks is more approachable.
To answer your question, I believe that the ball should be in tracks of equal length as drawn with pi=3.14xxx. And that we should try and eliminate all kinds of energy loss, if its a significant energy loss, and see where the balls move compared to a grid embedded into the tracks. The grid for Steven was the markings at each quarter of circumfrence. The data would be video, from above if possible and everything should be high frame rate and in focus, but that is a wishlist only.
From there I would analyze by where the ball passed markers and what the time was and compare the travel of the two balls. Beyond that all I have is no money for equipment, no time, and ice! Maybe I can join the club, but I have no video camera and no editing station [sigh] its just a dream. I didn't know as much as airman about precession and I will have to keep reviewing his nice diagrams. The math still eludes me but I cannot study it intensively and just kind of feel the frustration that I'm still on the fence if pi=4 or if there is something else going on. I don't know, it looks like the math is failing, but even that is a matter of interpreting experiment, I find that difficult.
3rd doorman- Posts : 25
Join date : 2020-04-03
 Re: PI NINE - Pi experiment with two edge track
Re: PI NINE - Pi experiment with two edge track
Having just re-read pi9.pdf, I see there is rolling radius now as well. I can't keep up, with RR or precession! I for sure thought of the squiggle before pi=9 came out, but still nobody is able to fully account for how the angular momentum is forced to undergo changes in the curved track that the straight track doesn't experience. Straight track has translational momentum but the axis of rotation stays perpendicular to the track and doesn't twist in space only moving through space in plane and in a line. but the curved track twists that axis around, there may not be enough energy lost due to precession there to explain the observed behaviors. I just can't say I have a handle on it yet. Miles claims he has proof, but I cannot understand the proof. I'm more an experimentalist, I just wish I could see the experiment repeated, or improved upon.
another thing no one has mentioned that I remember is to somehow anodize the ball to be half shiny and half white so that rolling might give us a smidgen more data, and if rolling is eliminated that would be evident. I think a track of ice that slides might bring still more precision, I just can't do it myself unfortunately. I can't even mock up diagrams, and have to use only wordy descriptions.
another thing no one has mentioned that I remember is to somehow anodize the ball to be half shiny and half white so that rolling might give us a smidgen more data, and if rolling is eliminated that would be evident. I think a track of ice that slides might bring still more precision, I just can't do it myself unfortunately. I can't even mock up diagrams, and have to use only wordy descriptions.
3rd doorman- Posts : 25
Join date : 2020-04-03
 Re: PI NINE - Pi experiment with two edge track
Re: PI NINE - Pi experiment with two edge track
.
Hi 3rd doorman, thanks for joining the discussion. And thanks for the positive feedback on my diagrams. They started as copies from Professor Lewin’s precession lecture but they are not correct with respect to the changes Miles has said need to be made to mainstream's current understanding of angular momentum.
I agree with some of your suggestions and frustrations, the ones I understand that is. Even cats-eye glass marbles would have provided more rolling axis information than a stainless steel ball bearing. In addition to the clear transparent pvc tubing, tubing with an internal mesh fabric “grid” is also available, but those changes would require a better video setup than a hand held i-phone.
Sure, there may be squiggles or wobble to the ball’s path, and frictional losses. I have no idea what replacing the ball with sliding ice might show except increased track resistance.
Cr6 has suggested the idea of building up atomic sized balls and tracks before, and I don’t quite understand that either, I assume that pi=4 for curved motion exists at any scale.
Don’t get too frustrated. I’ve been working at understanding Steven’s experiment for over ten years. I wonder why Miles has not acknowledged that precession must turn the curved tube track ball’s spin axis. In the meantime jfmeyer has something to say about a true mathematical kinematic Pi=4 “proof”.
.
Hi 3rd doorman, thanks for joining the discussion. And thanks for the positive feedback on my diagrams. They started as copies from Professor Lewin’s precession lecture but they are not correct with respect to the changes Miles has said need to be made to mainstream's current understanding of angular momentum.
I agree with some of your suggestions and frustrations, the ones I understand that is. Even cats-eye glass marbles would have provided more rolling axis information than a stainless steel ball bearing. In addition to the clear transparent pvc tubing, tubing with an internal mesh fabric “grid” is also available, but those changes would require a better video setup than a hand held i-phone.
Sure, there may be squiggles or wobble to the ball’s path, and frictional losses. I have no idea what replacing the ball with sliding ice might show except increased track resistance.
Cr6 has suggested the idea of building up atomic sized balls and tracks before, and I don’t quite understand that either, I assume that pi=4 for curved motion exists at any scale.
Don’t get too frustrated. I’ve been working at understanding Steven’s experiment for over ten years. I wonder why Miles has not acknowledged that precession must turn the curved tube track ball’s spin axis. In the meantime jfmeyer has something to say about a true mathematical kinematic Pi=4 “proof”.
.
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
 Re: PI NINE - Pi experiment with two edge track
Re: PI NINE - Pi experiment with two edge track
LongtimeAirman wrote:.
Hi 3rd doorman, thanks for joining the discussion. And thanks for the positive feedback on my diagrams. They started as copies from Professor Lewin’s precession lecture but they are not correct with respect to the changes Miles has said need to be made to mainstream's current understanding of angular momentum.
I agree with some of your suggestions and frustrations, the ones I understand that is. Even cats-eye glass marbles would have provided more rolling axis information than a stainless steel ball bearing. In addition to the clear transparent pvc tubing, tubing with an internal mesh fabric “grid” is also available, but those changes would require a better video setup than a hand held i-phone.
Sure, there may be squiggles or wobble to the ball’s path, and frictional losses. I have no idea what replacing the ball with sliding ice might show except increased track resistance.
Cr6 has suggested the idea of building up atomic sized balls and tracks before, and I don’t quite understand that either, I assume that pi=4 for curved motion exists at any scale.
Don’t get too frustrated. I’ve been working at understanding Steven’s experiment for over ten years. I wonder why Miles has not acknowledged that precession must turn the curved tube track ball’s spin axis. In the meantime jfmeyer has something to say about a true mathematical kinematic Pi=4 “proof”.
.
Yeah LTAM I just wanted to start with "balls" and tracks that can't scale down any further. Basically how does it roll at that level? Is it photons or atoms touching for the changes with the ball?
Chromium6- Posts : 818
Join date : 2019-11-29
 Re: PI NINE - Pi experiment with two edge track
Re: PI NINE - Pi experiment with two edge track
You said ice would increase track resistance. I propsed ice ball in plastic tube, on metal chanels, and on ice tube, and ice chanels. Also plain metal ball on ice.
I'm willing to lubricate the ice as well. The goal is to permit the ball to roll AND slide, and I can increase the weight of the ball to 3cm steel bearing with a coat of ice.
Do you think it could produce useful data if I was a wizard with a camera cell phone?
another apparatus. no straight track. just tube and metal channels. Both do a quarter circle, one radius twice the other one. Useful data?
I'm willing to lubricate the ice as well. The goal is to permit the ball to roll AND slide, and I can increase the weight of the ball to 3cm steel bearing with a coat of ice.
Do you think it could produce useful data if I was a wizard with a camera cell phone?
another apparatus. no straight track. just tube and metal channels. Both do a quarter circle, one radius twice the other one. Useful data?
3rd doorman- Posts : 25
Join date : 2020-04-03
 Re: PI NINE - Pi experiment with two edge track
Re: PI NINE - Pi experiment with two edge track
.
I'd say Miles’ pi9 paper provides us with a negative finding – which does not show "kinematic Pi equals 4". The experiment fails because of its slotted track. Instead of a single contact point between the ball and tube track, on the slotted track the ball rolls on two contact points - on the slot edges, call them left and right on the straight track and inside and outside edges with respect to the track center for the circular track.
The first problem with the slot track is the fact that the slot width allows the ball to roll below the top of the slot, resulting in a rolling radius smaller than the ball radius. This effectively reduces the ball’s forward velocity, the slotted track balls are not as fast as the tube track balls. Second, the circular slot track’s outside edge feels a greater gravitational and centripetal force, so the ball is mostly rolling on its outside edge which feels increased rolling friction, and increased ball sliding of the on the slot’s inside edge. Miles also talks about increased freedom on the ball’s outside edge. Third, the slotted track provides the energy necessary to turn the ball’s spin axis; in the tube track, I believe gravity based precession turns the ball’s spin axis about the circular track center.
Given all that, I believe we want rolling balls as in both Steven Oostijk’s and the pi9 experiment. The ball just happens to not roll well in the pi9 experiment. A rolling ball has both linear and angular momentum. There needs to be enough rolling friction in order to maintain ball/track contact without sliding on either straight or circular tracks. Why would you wish to reduce the ball’s rolling friction? True, we might want to increase the balls’ velocities and so increase their final or exit velocities, it shouldn't affect the pi=4 distance traveled outcome. Reducing friction may cause sliding. A ball sliding without rolling might provide additional data, you’d be creating a new and different pi=4 experiment, comparable to firing bullets into tube tracks, where the bullets would have no (rolling) angular momentum. The result may be a great deal of friction applied to the bullet in contact with the circular track’s outer edge and no friction felt by the bullet in the straight track, I believe sliding and rolling greatly complicates the experiment. Likely resulting in another another negative pi=4 outcome.
3rd doorman wrote. You said ice would increase track resistance. I propsed ice ball in plastic tube, on metal chanels, and on ice tube, and ice chanels. Also plain metal ball on ice.
Airman. Why do you think ice reduces friction?
Why is ice so slippery?
Nov 5, 2019
]https://www.sciencedaily.com/releases/2019/11/191105104416.htm#:~:text=The%20%22slippery%22%20nature%20of%20ice,top%20of%20this%20liquid%20film.&text=The%20mystery%20of%20sliding%20on,of%20this%20film%20of%20water.]
Airman. I don’t believe ice would reduce the contact point friction between the balls and their tracks. Friction must be present in order to melt the ice that results in what we perceive as ice’s slipperiness. Melting ice may in fact greatly increase the experiment’s complexity.
3rd doorman wrote. I'm willing to lubricate the ice as well. The goal is to permit the ball to roll AND slide, and I can increase the weight of the ball to 3cm steel bearing with a coat of ice.
Airman. The ball in the curved slot tracks already rolls and slides. Rolling and sliding in the circular tube track tube track is again a new experiment that will likely not show a pi=4 result.
3rd doorman wrote. Do you think it could produce useful data if I was a wizard with a camera cell phone?
Airman. Certainly, although I would urge you to not conduct an ice coated experiment. No wizardry skills necessary, just a camera cell phone, maybe a tripod, or enlist an able assistant.
3rd doorman wrote. another apparatus. no straight track. just tube and metal channels. Both do a quarter circle, one radius twice the other one. Useful data?
Airman. I don’t believe so. We run both straight and curved tracks in order to show that the balls arrive at the four diameter marker destinations (or a straight 2r track to compare with the quarter track circumference) at the same time, thus showing pi=4. Comparing quarter circle tracks of different types in a 2:1 radius difference can only demonstrate performance differences between quarter circles, quarter circle tracks with a 2:1 radius difference would be expected to have 2:1 lengths.
////\\\//\//\\\////\\\\\//////
Cr6 wrote. Yeah LTAM I just wanted to start with "balls" and tracks that can't scale down any further. Basically how does it roll at that level? Is it photons or atoms touching for the changes with the ball?
Airman. Sorry Cr6, I’d say we cannot scale Steven Oostijk’s balls and tracks down to anywhere near atomic lengths and expect the same results.
The pi=4 experiment with 3/8” balls is perfectly good at our scale, call it one meter. Understanding that the meter scale is halfway between the charge dominant forces of smaller scales, and the gravity dominant larger scales. The pi=4 experiment depends on gravity, first to bring the balls up to their starting velocities (a ramp), and second, to maintain good ball/track rolling contact points, i.e, with neither too much friction and no sliding. I also believe that gravity precesses the balls around circular tube track. Maybe the pi=4 experiment could work fine for millimeter radius balls and corresponding tracks sizes, but we cannot get much smaller before the pi=4 experiment “as designed” fails in some way. Pi=4, curved motion exists at all matter scales, but an experiment which shows pi=4 would need to be designed in accordance with the scale it will operate in. i.e, I don't believe atoms can roll like a ball on any atomic track, charge emissions would prevent contact, nor do I believe large spherical molecules can roll like a ball on a molecular track, for the same reason.
Am I getting any closer?
.
I'd say Miles’ pi9 paper provides us with a negative finding – which does not show "kinematic Pi equals 4". The experiment fails because of its slotted track. Instead of a single contact point between the ball and tube track, on the slotted track the ball rolls on two contact points - on the slot edges, call them left and right on the straight track and inside and outside edges with respect to the track center for the circular track.
The first problem with the slot track is the fact that the slot width allows the ball to roll below the top of the slot, resulting in a rolling radius smaller than the ball radius. This effectively reduces the ball’s forward velocity, the slotted track balls are not as fast as the tube track balls. Second, the circular slot track’s outside edge feels a greater gravitational and centripetal force, so the ball is mostly rolling on its outside edge which feels increased rolling friction, and increased ball sliding of the on the slot’s inside edge. Miles also talks about increased freedom on the ball’s outside edge. Third, the slotted track provides the energy necessary to turn the ball’s spin axis; in the tube track, I believe gravity based precession turns the ball’s spin axis about the circular track center.
Given all that, I believe we want rolling balls as in both Steven Oostijk’s and the pi9 experiment. The ball just happens to not roll well in the pi9 experiment. A rolling ball has both linear and angular momentum. There needs to be enough rolling friction in order to maintain ball/track contact without sliding on either straight or circular tracks. Why would you wish to reduce the ball’s rolling friction? True, we might want to increase the balls’ velocities and so increase their final or exit velocities, it shouldn't affect the pi=4 distance traveled outcome. Reducing friction may cause sliding. A ball sliding without rolling might provide additional data, you’d be creating a new and different pi=4 experiment, comparable to firing bullets into tube tracks, where the bullets would have no (rolling) angular momentum. The result may be a great deal of friction applied to the bullet in contact with the circular track’s outer edge and no friction felt by the bullet in the straight track, I believe sliding and rolling greatly complicates the experiment. Likely resulting in another another negative pi=4 outcome.
3rd doorman wrote. You said ice would increase track resistance. I propsed ice ball in plastic tube, on metal chanels, and on ice tube, and ice chanels. Also plain metal ball on ice.
Airman. Why do you think ice reduces friction?
Why is ice so slippery?
Nov 5, 2019
]https://www.sciencedaily.com/releases/2019/11/191105104416.htm#:~:text=The%20%22slippery%22%20nature%20of%20ice,top%20of%20this%20liquid%20film.&text=The%20mystery%20of%20sliding%20on,of%20this%20film%20of%20water.]
The "slippery" nature of ice is generally attributed to the formation of a thin layer of liquid water generated by friction, which for instance allows an ice skater to "surf" on top of this liquid film. ... The mystery of sliding on ice can therefore be found in the "viscous" nature of this film of water.
Airman. I don’t believe ice would reduce the contact point friction between the balls and their tracks. Friction must be present in order to melt the ice that results in what we perceive as ice’s slipperiness. Melting ice may in fact greatly increase the experiment’s complexity.
3rd doorman wrote. I'm willing to lubricate the ice as well. The goal is to permit the ball to roll AND slide, and I can increase the weight of the ball to 3cm steel bearing with a coat of ice.
Airman. The ball in the curved slot tracks already rolls and slides. Rolling and sliding in the circular tube track tube track is again a new experiment that will likely not show a pi=4 result.
3rd doorman wrote. Do you think it could produce useful data if I was a wizard with a camera cell phone?
Airman. Certainly, although I would urge you to not conduct an ice coated experiment. No wizardry skills necessary, just a camera cell phone, maybe a tripod, or enlist an able assistant.
3rd doorman wrote. another apparatus. no straight track. just tube and metal channels. Both do a quarter circle, one radius twice the other one. Useful data?
Airman. I don’t believe so. We run both straight and curved tracks in order to show that the balls arrive at the four diameter marker destinations (or a straight 2r track to compare with the quarter track circumference) at the same time, thus showing pi=4. Comparing quarter circle tracks of different types in a 2:1 radius difference can only demonstrate performance differences between quarter circles, quarter circle tracks with a 2:1 radius difference would be expected to have 2:1 lengths.
////\\\//\//\\\////\\\\\//////
Cr6 wrote. Yeah LTAM I just wanted to start with "balls" and tracks that can't scale down any further. Basically how does it roll at that level? Is it photons or atoms touching for the changes with the ball?
Airman. Sorry Cr6, I’d say we cannot scale Steven Oostijk’s balls and tracks down to anywhere near atomic lengths and expect the same results.
The pi=4 experiment with 3/8” balls is perfectly good at our scale, call it one meter. Understanding that the meter scale is halfway between the charge dominant forces of smaller scales, and the gravity dominant larger scales. The pi=4 experiment depends on gravity, first to bring the balls up to their starting velocities (a ramp), and second, to maintain good ball/track rolling contact points, i.e, with neither too much friction and no sliding. I also believe that gravity precesses the balls around circular tube track. Maybe the pi=4 experiment could work fine for millimeter radius balls and corresponding tracks sizes, but we cannot get much smaller before the pi=4 experiment “as designed” fails in some way. Pi=4, curved motion exists at all matter scales, but an experiment which shows pi=4 would need to be designed in accordance with the scale it will operate in. i.e, I don't believe atoms can roll like a ball on any atomic track, charge emissions would prevent contact, nor do I believe large spherical molecules can roll like a ball on a molecular track, for the same reason.
Am I getting any closer?
.
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
Chromium6 likes this post
 Re: PI NINE - Pi experiment with two edge track
Re: PI NINE - Pi experiment with two edge track
That was just a thought experiment--the scaling down. I was thinking of something similar to this:
DNA nanoball sequencing
https://en.m.wikipedia.org/wiki/DNA_nanoball_sequencing
or something like this:
http://www.nanotech-now.com/nanotube-buckyball-sites.htm
DNA nanoball sequencing
https://en.m.wikipedia.org/wiki/DNA_nanoball_sequencing
or something like this:
http://www.nanotech-now.com/nanotube-buckyball-sites.htm
Chromium6- Posts : 818
Join date : 2019-11-29
 Similar topics
Similar topics» More on the running track
» On the track of unconventional superconductivity, researchers are charting unknown territory
» Animate the PI = 4 experiment
» How about an Experiment to Simulate Attraction?
» The Event Horizon Telescope experiment
» On the track of unconventional superconductivity, researchers are charting unknown territory
» Animate the PI = 4 experiment
» How about an Experiment to Simulate Attraction?
» The Event Horizon Telescope experiment
Page 1 of 1
Permissions in this forum:
You cannot reply to topics in this forum