Possible Charged Particle Field
4 posters
Page 14 of 15
Page 14 of 15 •  1 ... 8 ... 13, 14, 15
1 ... 8 ... 13, 14, 15 
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
.
I’ve forgotten the source of the EQS algorithm. I’ve cited it here somewhere at the site but I’ve been unable to find it. Anyway,
It occurred to me that the particle ring algorithm could serve perfectly well to generate latitude particle positions (as well as longitudinal) better than the EQS latitude particle ring currently does, because it isn't constrained to r=1 surface particles only. I believe our new pRing algorithm can easily replace the EQS algorithm. What a strange coincidence.
And not just precision charge detector locations, maybe the Precision points could be modeled as charge emission points.
.
I’ve forgotten the source of the EQS algorithm. I’ve cited it here somewhere at the site but I’ve been unable to find it. Anyway,
It occurred to me that the particle ring algorithm could serve perfectly well to generate latitude particle positions (as well as longitudinal) better than the EQS latitude particle ring currently does, because it isn't constrained to r=1 surface particles only. I believe our new pRing algorithm can easily replace the EQS algorithm. What a strange coincidence.
And not just precision charge detector locations, maybe the Precision points could be modeled as charge emission points.
.
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
While the EQS algorithm does generate points at r=1, it is not limited to that. The algorithm could easily be changed to use any radius. Actually, I just checked the code and it already does take in a radius to generate the points at.
The EQS algorithm was chosen because it generates points that are very close to being equidistant from each other. This algorithm does not have that property. The charge points require that because they represent the locations that external charge is felt from. We want that to evenly cover the surface of the sphere or we are going to get very strange results.
It is good to see you thinking in this way though. You're seeing how to use things to your advantage. Seeing a bigger picture and how you can use smaller pieces to accomplish what you want to.
The EQS algorithm was chosen because it generates points that are very close to being equidistant from each other. This algorithm does not have that property. The charge points require that because they represent the locations that external charge is felt from. We want that to evenly cover the surface of the sphere or we are going to get very strange results.
It is good to see you thinking in this way though. You're seeing how to use things to your advantage. Seeing a bigger picture and how you can use smaller pieces to accomplish what you want to.
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
.
I had no idea the EQS algorithm worked with equi-areas, do you recall the citation? I would think the radius you entered into EQS would apply to all the surface particles. As you yourself mentioned, the new particle ring algorithm could actually include different radii at the same time.

I put this diagram together to help clarify things. The blue lines are the latitude rings that the particles are centered on, except for the pole particles which appear to be centered on an edge of the vertical latitude extent.
I do enjoy working with this stuff.
.
I had no idea the EQS algorithm worked with equi-areas, do you recall the citation? I would think the radius you entered into EQS would apply to all the surface particles. As you yourself mentioned, the new particle ring algorithm could actually include different radii at the same time.

I put this diagram together to help clarify things. The blue lines are the latitude rings that the particles are centered on, except for the pole particles which appear to be centered on an edge of the vertical latitude extent.
I do enjoy working with this stuff.
.
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
.
Ok, here's the source, below. I recall reading the short paper, it's just a few years old, based on distributing equi-area rectangles on the surface of a sphere. Of course, we are distributing spherical particles, or circular areas and not rectangles and so I treat the equi-area claim with much skepticism. It appears that the second source is an application based on the same partitioning ideas as the paper, although the application is ten years older than the paper. The application is chock full of code and was beyond me when I first looked at it. The page claims only two downloads in the last 13 years or so; did you download one of them? I'll try studying it a bit.
A new method to subdivide a spherical surface into equal-area cells by Zinovy Malkin. https://arxiv.org/ftp/arxiv/papers/1612/1612.03467.pdf
Abstract. A new method is proposed to divide a spherical surface into equal-area cells. The method is based on dividing a sphere into several latitudinal bands of near-constant span with further division of each band into equal-area cells. It is simple in construction and provides more uniform latitude step between latitudinal bands than other methods of isolatitudinal equal-area tessellation of a spherical surface.
https://www.mathworks.com/matlabcentral/fileexchange/13356-eqsp-recursive-zonal-sphere-partitioning-toolbox
EQSP: Recursive Zonal Sphere Partitioning Toolbox. A suite of Matlab functions intended for use in exploring equal area sphere partitioning.
///////////////////////////////////////////////
PS. If we were truly interested in covering the sphere with equi-areas for charge density/distribution purposes - say to provide at least 3 or 4 precision alternatives - I 'know' I can improve the output performance of the EQS algorithm by replacing the current equi-area rectangles with hexagons. For example, look at the EQS equators which present columns of particles - I rationalized it by saying they shared axial charge channels. We can increase the number of particle spheres by offsetting alternate latitude rows, positioning the particle spheres hexagonally, more like alternate bricks in a wall, instead of the current particle columns.
I'll work on a proper example.
.
Ok, here's the source, below. I recall reading the short paper, it's just a few years old, based on distributing equi-area rectangles on the surface of a sphere. Of course, we are distributing spherical particles, or circular areas and not rectangles and so I treat the equi-area claim with much skepticism. It appears that the second source is an application based on the same partitioning ideas as the paper, although the application is ten years older than the paper. The application is chock full of code and was beyond me when I first looked at it. The page claims only two downloads in the last 13 years or so; did you download one of them? I'll try studying it a bit.
A new method to subdivide a spherical surface into equal-area cells by Zinovy Malkin. https://arxiv.org/ftp/arxiv/papers/1612/1612.03467.pdf
Abstract. A new method is proposed to divide a spherical surface into equal-area cells. The method is based on dividing a sphere into several latitudinal bands of near-constant span with further division of each band into equal-area cells. It is simple in construction and provides more uniform latitude step between latitudinal bands than other methods of isolatitudinal equal-area tessellation of a spherical surface.
https://www.mathworks.com/matlabcentral/fileexchange/13356-eqsp-recursive-zonal-sphere-partitioning-toolbox
EQSP: Recursive Zonal Sphere Partitioning Toolbox. A suite of Matlab functions intended for use in exploring equal area sphere partitioning.
///////////////////////////////////////////////
PS. If we were truly interested in covering the sphere with equi-areas for charge density/distribution purposes - say to provide at least 3 or 4 precision alternatives - I 'know' I can improve the output performance of the EQS algorithm by replacing the current equi-area rectangles with hexagons. For example, look at the EQS equators which present columns of particles - I rationalized it by saying they shared axial charge channels. We can increase the number of particle spheres by offsetting alternate latitude rows, positioning the particle spheres hexagonally, more like alternate bricks in a wall, instead of the current particle columns.
I'll work on a proper example.
.
Last edited by LongtimeAirman on Wed Feb 06, 2019 1:48 pm; edited 2 times in total (Reason for editing : Added PS.)
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
.
The EQS group consists of 46, 130 and 406 spherical equi-iso-latitudinal areas, which you've replaced with “points”, used for calculating charge received by our charge field particles. I believe the equi-area claim is great for Cartesian maps; however, the equi area claim with respect to points is false. How do I prove it?

EQS Packing r=1 particles , making up an r=10 sphere. How many particles can we fit without overlap?
I’ve made a game of packing r=1 neutral particles onto a r=10 spherical surface without overlap. I submit that the maximal contender using the EQS algorithm is EQS238. I posted an image of it on Monday, on the bottom of the last page of this thread, here it is again above. EQS238 is on the right side, a little too large to see here.
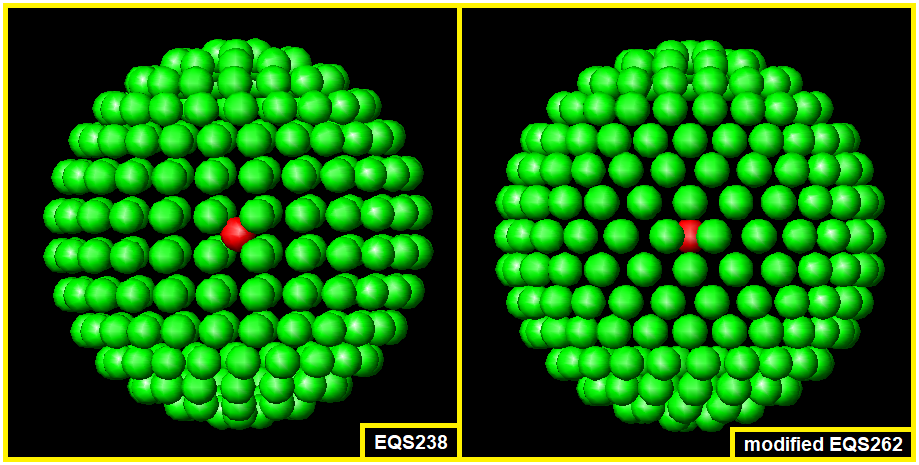
I recreated the EQS238 in autocad, without foreshortening. Note that that EQS238 has six latitude particle rings of 24 particles about the equator. The particles are arranged in longitudinal lines. By offsetting alternate rows, changing from from 15 to 11 degree latitude steps while maintaining a 15 degree spacing between particles in that equatorial band, I was able to add a seventh row of 24 particles directly over the equator to result in the modified EQS262. Having increased the particle count by 24 you might agree that the equi-area particle distribution of 262 is somewhat improved over EQS232.
I admit, its a bit hit or miss. But i definitely want to improve the distribution of our charge detection points. If you like, I'll go through this exercise again with EQS406.
.
The EQS group consists of 46, 130 and 406 spherical equi-iso-latitudinal areas, which you've replaced with “points”, used for calculating charge received by our charge field particles. I believe the equi-area claim is great for Cartesian maps; however, the equi area claim with respect to points is false. How do I prove it?

EQS Packing r=1 particles , making up an r=10 sphere. How many particles can we fit without overlap?
I’ve made a game of packing r=1 neutral particles onto a r=10 spherical surface without overlap. I submit that the maximal contender using the EQS algorithm is EQS238. I posted an image of it on Monday, on the bottom of the last page of this thread, here it is again above. EQS238 is on the right side, a little too large to see here.

I recreated the EQS238 in autocad, without foreshortening. Note that that EQS238 has six latitude particle rings of 24 particles about the equator. The particles are arranged in longitudinal lines. By offsetting alternate rows, changing from from 15 to 11 degree latitude steps while maintaining a 15 degree spacing between particles in that equatorial band, I was able to add a seventh row of 24 particles directly over the equator to result in the modified EQS262. Having increased the particle count by 24 you might agree that the equi-area particle distribution of 262 is somewhat improved over EQS232.
I admit, its a bit hit or miss. But i definitely want to improve the distribution of our charge detection points. If you like, I'll go through this exercise again with EQS406.
.
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
Airman wrote:As you yourself mentioned, the new particle ring algorithm could actually include different radii at the same time.
I didn't mean it would use different radii at the same time. Currently, it uses the same radius for all points generated in a single call of the function. It could be changed to generate different radii, but that is not what it needs to do for its current use, and I wouldn't change it that way anyway. It is best left as it is and you change the points in another function. One function generates points (or handles direction) while the other moves them in and/or out in whatever way you want (handling distance). That way, you can exchange either algorithm for another without affecting the other one. Keeping your code small and concise and modular allows it to be re-usable. If your code is intimately tied into what you want it to do in this one case, then it is difficult to pull it out for a different need. It takes a while, but you get a feel for these kinds of things.
Here's another paper that is more specific to our need to generate charge points.
https://www.cmu.edu/biolphys/deserno/pdf/sphere_equi.pdf
We'd want the regular placement version. Simple algorithm. Probably a better result than the EQS algorithm when using it for points. If you want to implement it, find the current eqs.js file and create another one in the same directory. Copy this code into it and implement the createLocations function.
- Code:
var EquidistantSphericalPoints = (function( THREE, SPHERE )
{
var module = Object.create( {}, {
Version: { value: '0.1', writable: false }
} );
/**
* A ChargePointLocator is used to create a collection of ChargePoints
* that can work together for a sphere
*/
module.LocationCreator = function()
{
SPHERE.LocationCreator.call( this );
// TODO add properties that control the algorithm here
// e.g. this.area = 1;
};
module.LocationCreator.prototype = Object.create( SPHERE.LocationCreator.prototype, {
constructor: { value: module.LocationCreator, writable: false }
} );
module.LocationCreator.prototype.createLocations = function( radius, dst )
{
// TODO generate points at radius and push into dst
};
return module;
}( THREE, SPHERE ));
Look at EQS to get a general idea of what you need to do, but the algorithm itself is quite different.
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
What I am looking for with this algorithm is uniformity. I'm not too concerned with covering the entire surface with charge points. I just want whatever charge points are in use to be uniformly distributed over that surface. Your EQS262 covers the equatorial region beautifully, but it has problems at the poles. You can clearly see where it changes from equator to pole at about half way up the surface. The standard EQS has problems at the poles too, so does this algorithm, so do all of them.
I wonder if you could alter 262, or something close to that, to just offset every second row. Don't add any more rows in, just offset every even row or something like that. Try to get more of the surface to be in that diamond pattern rather than columns. You might be able to get a bit closer to what we need.
I wonder if you could alter 262, or something close to that, to just offset every second row. Don't add any more rows in, just offset every even row or something like that. Try to get more of the surface to be in that diamond pattern rather than columns. You might be able to get a bit closer to what we need.
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
.
Affirmative, we want a uniform distribution of surface points. Given my example converting EQS238 to the Modified-EQS262, I thought I might be able to alter or optimize a given EQS set, making the same custom changes I made with autocad, including particle ring rotations of a few degrees. And so I'd work on EQS46, 130, and 406 with that goal in mind.
As far as EQS goes, it seems that as the number of areas is increased, the more accurate the algorithm becomes. I noticed the three polar points, a sure sign that the algorithm isn’t based on a regular polyhedron. Unfortunately, the lower number EQS algorithm solutions seem to place the greatest concentration of points about the poles. Still, I noticed there are pole area rings which would also benefit from particle ring offset rotations. Note that the separation between the three particle and 9 particle ring sets is currently at minimum, and can be increased with a 45deg rotation. Of course, i'll need to find out if I can alter the EQS code or not.
Actually, I had a better solution in mind. I was going geodesic on our charge particle.
Geodesic polyhedron https://en.wikipedia.org/wiki/Geodesic_polyhedron
I have the vertices, edges and edge arcs for the basic icosa and octahedron plotted. I’d started the second frequency subdivisions when I read your link.
https://www.cmu.edu/biolphys/deserno/pdf/sphere_equi.pdf
At first it seemed too simple to believe. A single page, illustrated, including notes, a refresher on spherical coordinates, formulas, algorithms and references. A half dozen or more reads later and despite the fact that there are three points at the poles, I can’t wait to try this new code and test it at r=10 with the rest.
I’m overwhelmed - delighted - at the possibilities. In any case, I'll give it a go.
.
Affirmative, we want a uniform distribution of surface points. Given my example converting EQS238 to the Modified-EQS262, I thought I might be able to alter or optimize a given EQS set, making the same custom changes I made with autocad, including particle ring rotations of a few degrees. And so I'd work on EQS46, 130, and 406 with that goal in mind.
As far as EQS goes, it seems that as the number of areas is increased, the more accurate the algorithm becomes. I noticed the three polar points, a sure sign that the algorithm isn’t based on a regular polyhedron. Unfortunately, the lower number EQS algorithm solutions seem to place the greatest concentration of points about the poles. Still, I noticed there are pole area rings which would also benefit from particle ring offset rotations. Note that the separation between the three particle and 9 particle ring sets is currently at minimum, and can be increased with a 45deg rotation. Of course, i'll need to find out if I can alter the EQS code or not.
Actually, I had a better solution in mind. I was going geodesic on our charge particle.
Geodesic polyhedron https://en.wikipedia.org/wiki/Geodesic_polyhedron
I have the vertices, edges and edge arcs for the basic icosa and octahedron plotted. I’d started the second frequency subdivisions when I read your link.
https://www.cmu.edu/biolphys/deserno/pdf/sphere_equi.pdf
At first it seemed too simple to believe. A single page, illustrated, including notes, a refresher on spherical coordinates, formulas, algorithms and references. A half dozen or more reads later and despite the fact that there are three points at the poles, I can’t wait to try this new code and test it at r=10 with the rest.
I’m overwhelmed - delighted - at the possibilities. In any case, I'll give it a go.
.
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
Those geodesics do look promising. Worth a try at some point. I like the triangulation approach. I've done that before to generate spheres from dodecahedrons (or maybe icosahedrons) and it does work well. Whether it gives us the required conformity, I don't know, but it looks like it might. It is always interesting to try different algorithms and see their differences.
Negative. Don't alter that code, create a new implementation so that we can swap them with ease. A couple of posts above I have written the boilerplate code for a new charge point location generator. Find the existing eqs.js file, create a new JS file in that directory for your new implementation and copy the code above into it. Then change the name on the top line, EquidistantSphericalPoints in the above code, to something that reflects the algorithm. Then just implement the module.LocationCreator.prototype.createLocations function. That function is given the radius to create points at and an array that you add THREE.Vector3 objects to. The rest of the application already knows how to use it and just needs to be told to use a particular implementation.
Airman wrote:Of course, i'll need to find out if I can alter the EQS code or not.
Negative. Don't alter that code, create a new implementation so that we can swap them with ease. A couple of posts above I have written the boilerplate code for a new charge point location generator. Find the existing eqs.js file, create a new JS file in that directory for your new implementation and copy the code above into it. Then change the name on the top line, EquidistantSphericalPoints in the above code, to something that reflects the algorithm. Then just implement the module.LocationCreator.prototype.createLocations function. That function is given the radius to create points at and an array that you add THREE.Vector3 objects to. The rest of the application already knows how to use it and just needs to be told to use a particular implementation.
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
.
Per your directions, thank you very much, I copied eqs.js to a new file sphericalpoints.js, and replaced the contents with your above - var EquidistantSphericalPoints. Is the name difference a problem?
I have 2 or 3 goals. First is to figure out how to create and use the new equidistant points on a sphere algorithm.
Second, I assume I may corrupt the EQS function, or should I could create another duplicate EQS file for "EQS-optimization"?
Third, the geodesic contender may emerge. I had high hopes at first, but they are fading as I realize that a low frequency geodesic solution for uniform distribution of points is unlikely. Yesterday and today I've played with the 1st and 2nd frequency sets for both the icosahedon and octahedrons and saw a huge flaw in my expectations. The reason the EQS algorithm is not a good solution is that it divides a sphere surface into equi-iso-latitudinal areas and Not points; Geodesics is 'probably' not a good solution as it divides spheres into chords, and Not points. I haven’t figured out how best to convert geodesic areas/lines into points or whether the exercise is completely pointless.
Unless directed otherwise, I’ll use a Spherical scenario to call the new appropriate algorithm in order to position N neutral, unmoveable particles and so compare the various alternates.
Again, I appreciate the directions.
.
Per your directions, thank you very much, I copied eqs.js to a new file sphericalpoints.js, and replaced the contents with your above - var EquidistantSphericalPoints. Is the name difference a problem?
I have 2 or 3 goals. First is to figure out how to create and use the new equidistant points on a sphere algorithm.
Second, I assume I may corrupt the EQS function, or should I could create another duplicate EQS file for "EQS-optimization"?
Third, the geodesic contender may emerge. I had high hopes at first, but they are fading as I realize that a low frequency geodesic solution for uniform distribution of points is unlikely. Yesterday and today I've played with the 1st and 2nd frequency sets for both the icosahedon and octahedrons and saw a huge flaw in my expectations. The reason the EQS algorithm is not a good solution is that it divides a sphere surface into equi-iso-latitudinal areas and Not points; Geodesics is 'probably' not a good solution as it divides spheres into chords, and Not points. I haven’t figured out how best to convert geodesic areas/lines into points or whether the exercise is completely pointless.
Unless directed otherwise, I’ll use a Spherical scenario to call the new appropriate algorithm in order to position N neutral, unmoveable particles and so compare the various alternates.
Again, I appreciate the directions.
.
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
The name difference is mandatory. We need to be able to identify different implementations and that name at the top of the file is how we do it. The name should reflect the algorithm being implemented. You can shorten it, like I have with EQS, as long as it is unique in the project.
To use the new code, you need to include it in the project by adding it to the HTML file. At the top, in the HEAD section, you will find the existing EQS import:
Copy and paste that directly below the existing one and then change eqs.js to the name of your JS file.
You create an instance and call its createLocations method like this:
The radius may be specified somewhere else and passed in, you wouldn't generally declare it like that and use it straight away (unless you had more uses for the value).
After that code has executed, the points array will contain THREE.Vector3 objects. You can use them in any way you want to. You can change them. Use the Vector3.multiplyScalar function to change the length without changing the direction.
No, you definitely can not change eqs.js (unless fixing a bug in it). It is being used, so if you change it, it will change that too and I don't want that. We can add new implementations all we want, but we can't change what is being used unless it needs to happen.
With respect to the geodesics, don't worry about them talking about areas and triangles. All of these algorithms generate points, but those points are then used to build areas on the surface. Most times you can just use the points as generated, but sometimes, like in EQS, you do need to think about how to convert the area into a single point. When I looked at those geodesics, I was only looking at the points and their distribution on the sphere. Ignore the triangles, except in how they help you to see the distances between points. You may be right, they may turn out useless, but they might find some other use too.
To use the new code, you need to include it in the project by adding it to the HTML file. At the top, in the HEAD section, you will find the existing EQS import:
- Code:
<script src="js/engine/eqs.js"></script>
Copy and paste that directly below the existing one and then change eqs.js to the name of your JS file.
You create an instance and call its createLocations method like this:
- Code:
var radius = 10;
var points = [];
var locator = new EquidistantSphericalPoints.LocationCreator();
locator.createLocations( radius, points );
The radius may be specified somewhere else and passed in, you wouldn't generally declare it like that and use it straight away (unless you had more uses for the value).
After that code has executed, the points array will contain THREE.Vector3 objects. You can use them in any way you want to. You can change them. Use the Vector3.multiplyScalar function to change the length without changing the direction.
No, you definitely can not change eqs.js (unless fixing a bug in it). It is being used, so if you change it, it will change that too and I don't want that. We can add new implementations all we want, but we can't change what is being used unless it needs to happen.
With respect to the geodesics, don't worry about them talking about areas and triangles. All of these algorithms generate points, but those points are then used to build areas on the surface. Most times you can just use the points as generated, but sometimes, like in EQS, you do need to think about how to convert the area into a single point. When I looked at those geodesics, I was only looking at the points and their distribution on the sphere. Ignore the triangles, except in how they help you to see the distances between points. You may be right, they may turn out useless, but they might find some other use too.
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
.
I was able to get the new Equi-distant Spherical Points algorithm to work in its own scenario initEQPSphereUI. EQP as opposed to the existing EQS. It's a simple matter to choose any number of particles and the spherical configuration's radius. Next I'll transfer the known good "working" EQP to sphericalpoints.js as previously directed.

Here's a direct comparison between the EQS406 and EQP406 algorithms; 406 r=1 particles in a r=20 sphere. The results are very similar, suggesting that it may take some effort to improve the uniformity of our particle engine's charge detection points.
.
I was able to get the new Equi-distant Spherical Points algorithm to work in its own scenario initEQPSphereUI. EQP as opposed to the existing EQS. It's a simple matter to choose any number of particles and the spherical configuration's radius. Next I'll transfer the known good "working" EQP to sphericalpoints.js as previously directed.

Here's a direct comparison between the EQS406 and EQP406 algorithms; 406 r=1 particles in a r=20 sphere. The results are very similar, suggesting that it may take some effort to improve the uniformity of our particle engine's charge detection points.
.
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
I would rename sphericalpoints.js to eqp.js and similar with the module name, just use EQP. Then it is a simple matter to swap between EQS and EQP.
It is a bit difficult to see the difference in those images. The particles in the back blur out the ones in the front. What you want to do is change the charge point algorithm to use this, instead of EQS. This is the reason I suggested you create a class for it. Both EQS and now EQP both implement the same interface, so we can use them interchangeably.
In /js/engine/charge-point-engine.js at line 450, you will find the createChargePointLocator function. This is responsible for creating the object that will generate charge point locations. It also hooks in to the menu through the module.ChargePointConfiguration property.
You can just change EQS to EQP and the app will use your algorithm to generate charge points. That will be a lot easier to see the differences in pics. If you want to, you can even add EQP as more choices in that switch statement so that you can swap between EQS and EQP without changing the source code. You will need to add them as options to the menu as well, which is in the HTML file at line 461.
You don't need to add the constants, like PIM_CHARGE_POINT_LOW. You can just use literal values here and in the switch statement above like this:
and
It is a bit difficult to see the difference in those images. The particles in the back blur out the ones in the front. What you want to do is change the charge point algorithm to use this, instead of EQS. This is the reason I suggested you create a class for it. Both EQS and now EQP both implement the same interface, so we can use them interchangeably.
In /js/engine/charge-point-engine.js at line 450, you will find the createChargePointLocator function. This is responsible for creating the object that will generate charge point locations. It also hooks in to the menu through the module.ChargePointConfiguration property.
- Code:
module.createChargePointLocator = function()
{
var locator = null;
switch( module.ChargePointConfiguration )
{
case module.CHARGE_POINT_LOW:
locator = new Hosohedron.LocationCreator( 4, 2 );
break;
case module.CHARGE_POINT_MEDIUM:
//locator = new Hosohedron.LocationCreator( 8, 4 );
locator = new EQS.LocationCreator( EQS.ANGLES_46 );
break;
case module.CHARGE_POINT_HIGH:
//locator = new Hosohedron.LocationCreator( 16, 8 );
locator = new EQS.LocationCreator( EQS.ANGLES_130 );
break;
case module.CHARGE_POINT_OVERDRIVE:
//locator = new Hosohedron.LocationCreator( 32, 16 );
locator = new EQS.LocationCreator( EQS.ANGLES_406 );
break;
default:
locator = new Hosohedron.LocationCreator( 4, 2 );
//locator = new EQS.LocationCreator( EQS.ANGLES_46 );
}
return locator;
};
You can just change EQS to EQP and the app will use your algorithm to generate charge points. That will be a lot easier to see the differences in pics. If you want to, you can even add EQP as more choices in that switch statement so that you can swap between EQS and EQP without changing the source code. You will need to add them as options to the menu as well, which is in the HTML file at line 461.
- Code:
folder1 = gui.addFolder( 'Precision' );
addCPCfg( PIM.CHARGE_POINT_LOW, 'Low', folder1 );
addCPCfg( PIM.CHARGE_POINT_MEDIUM, 'Medium', folder1 );
addCPCfg( PIM.CHARGE_POINT_HIGH, 'High', folder1 );
addCPCfg( PIM.CHARGE_POINT_OVERDRIVE, 'Overdrive', folder1 );
You don't need to add the constants, like PIM_CHARGE_POINT_LOW. You can just use literal values here and in the switch statement above like this:
- Code:
addCPCfg( 100, 'EQP Overdrive', folder1 );
and
- Code:
switch( module.ChargePointConfiguration )
{
case 100:
// TODO create EQP locator
break;
...
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
I added a comment to one of you recent commits, did you see that? Did you get an email about it? I wasn't sure what the site was going to do, so let me know.
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
.
I just looked at sourcetree and didn't see your commit comment - nothing too serious I hope. I've never received any e-mail notices from bitbucket.
Thanks for the additional guidance.
.
I just looked at sourcetree and didn't see your commit comment - nothing too serious I hope. I've never received any e-mail notices from bitbucket.
Thanks for the additional guidance.
.
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
.
I logged into bitbucket and saw your comment. Copy the initial letter name change. I see I did receive an e-mail from bitbucket eight hours ago. I usually just check my mail first thing every morning; I would have seen the bitbucket message tomorrow.
.
I logged into bitbucket and saw your comment. Copy the initial letter name change. I see I did receive an e-mail from bitbucket eight hours ago. I usually just check my mail first thing every morning; I would have seen the bitbucket message tomorrow.
.
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
Comments will only show on the BitBucket site, not through SourceTree or any other GIT client (that I am aware of).
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
.
Ok, status update.
EQP closely follows the EQS naming convention. We have eqp.js (like eqs.js) and new module var EQP (like var EQS). The names of the html and module must be different, I thought that the case change between eqs.js and var EQS somehow violated that rule; it's much cleaner now.
I believe I've followed 'all' your directions except: 1. Creating an instance and 2. Adding a "switch".
I assume the instances must be in eqp.js, so I'll add the new EQP alternatives CHARGE_POINT_46, CHARGE_POINT_130 and CHARGE_POINT_406 there. Just between you and me, I'm having a heck of a time trying to understand the LocationCreator.prototype.createLocations function.
PS. Corrected to "must be in eqp.js,". I'm making too many typos; the fidgets, sorry for that.
Heck as in difficult. First location then radius. I see that SPHERE.LocationCreator is the main module, used by both hosohedron.js and eqs.js. Both have instance examples.
.
Ok, status update.
EQP closely follows the EQS naming convention. We have eqp.js (like eqs.js) and new module var EQP (like var EQS). The names of the html and module must be different, I thought that the case change between eqs.js and var EQS somehow violated that rule; it's much cleaner now.
I believe I've followed 'all' your directions except: 1. Creating an instance and 2. Adding a "switch".
I assume the instances must be in eqp.js, so I'll add the new EQP alternatives CHARGE_POINT_46, CHARGE_POINT_130 and CHARGE_POINT_406 there. Just between you and me, I'm having a heck of a time trying to understand the LocationCreator.prototype.createLocations function.
PS. Corrected to "must be in eqp.js,". I'm making too many typos; the fidgets, sorry for that.
Heck as in difficult. First location then radius. I see that SPHERE.LocationCreator is the main module, used by both hosohedron.js and eqs.js. Both have instance examples.
.
Last edited by LongtimeAirman on Thu Feb 14, 2019 10:04 pm; edited 1 time in total (Reason for editing : Added PS.)
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
LongtimeAirman wrote:
The names of the html and module must be different, I thought that the case change between eqs.js and var EQS somehow violated that rule; it's much cleaner now.
I not exactly sure what you mean by 'html' there, but I assume you mean the name of the JS file, eqp.js in this case, which is included in the HTML file. That file name and the module name are totally unconnected, from a code perspective. In this case, and generally most cases, they will be related because the filename should reflect what it contains and the module should also reflect what it contains, so they will be fairly close. But there is no requirement that they be related as they are totally different things.
LongtimeAirman wrote:
I believe I've followed 'all' your directions except: 1. Creating an instance and 2. Adding a "switch".
I assume the instances must be in ecp.js., so I'll add the new EQP alternatives CHARGE_POINT_46, CHARGE_POINT_130 and CHARGE_POINT_406 there. Just between you and me, I'm having a heck of a time trying to understand the LocationCreator.prototype.createLocations function.
I don't want you to add a switch, I want you to add a case to the existing switch statement. You can see the other cases in the code snapshot I posted above, and you just need to add another case and break, creating your EQP object between them, just like all of the others. It looks like you will add 3 case statements, one for each size: 46, 130 and 406.
A switch statement works by evaluating an expression into some value. That value is then compared to all of the cases until a match is found. If a match is found, then the code inside that case is executed until a break statement is found (or the end of the switch statement). If it encounters a break statement, then it exits the switch and continues execution after it. Note that it is totally possible to let one case fall into another case by not having a break statement in the first. This is often useful, but if you didn't mean to do that, it can cause some funny bugs.
Suppose we had a value that is a string, let's say 'myString'. If we passed it to this switch statement:
- Code:
var value = 'myString';
switch( value )
{
case 'not the right case':
console.log( 'not this one' );
break;
case 'not this one either':
console.log( 'nope, wrong again' );
break;
case 'myString':
console.log( 'found it!' );
break;
case 'try again':
console.log( 'nada' );
break;
}
then we would see 'found it!' printed to the console and none of the other messages would be.
What would happen if the value did not match any of the cases? In the above switch, it would do nothing. If it doesn't match, then it doesn't have anything to execute, so it will just continue processing the code after the switch. However, you can add a default case that will get executed if no specific match is found:
- Code:
var value = 'won't match anything';
switch( value )
{
case 'not the right case':
console.log( 'not this one' );
break;
case 'not this one either':
console.log( 'nope, wrong again' );
break;
case 'myString':
console.log( 'found it!' );
break;
case 'try again':
console.log( 'nada' );
break;
default:
console.log( 'did not find any matching case' );
}
You can add a break after the default code, but you don't have to if it is the last case in the switch.
What if we had 2 cases that actually contain the same code? Then we omit the break statement from one and let it fall into the next:
- Code:
var value = 'won't match anything';
switch( value )
{
case 'not the right case':
console.log( 'not this one' );
break;
case 'not this one either':
console.log( 'nope, wrong again' );
break;
case 'myString':
case 'myOtherString':
console.log( 'found it!' );
break;
case 'try again':
console.log( 'nada' );
break;
default:
console.log( 'did not find any matching case' );
}
So if value is either 'myString' or 'myOtherString', it will show 'found it!' in the console. It is also possible to execute some code for 'myString' and still let it fall into 'myOtherString', if you have a need to do something extra for one and not the other.
- Code:
var value = 'won't match anything';
switch( value )
{
case 'not the right case':
console.log( 'not this one' );
break;
case 'not this one either':
console.log( 'nope, wrong again' );
break;
case 'myString':
console.log( 'it is myString' );
case 'myOtherString':
console.log( 'found it!' );
break;
case 'try again':
console.log( 'nada' );
break;
default:
console.log( 'did not find any matching case' );
}
So in this version, if value='myString', then it will print 'it is myString' and 'found it!' to the console, but only 'found it!' if value='myOtherString'.
The createLocations method just needs to create THREE.Vector3 objects and add them to the dst parameter, which is an array.
- Code:
module.LocationCreator.prototype.createLocations = function( radius, dst )
{
for( var i=0; i<10; i++ )
{
dst.push( new THREE.Vector3( i, i, i ) );
}
};
That is a trivial example, but it shows the intent of the method. I'll break it down to show what each part is doing.
module is the module object that will become EQP in your case, but it hasn't been set to the EQP variable yet, so we refer to it as module (which is a local variable, where-as EQP is global).
LocationCreator is a class, which is actually defined above this method declaration, but it looks like any other function. It is actually just a function, but when we call it with the new keyword in front of it, it is treated as a class constructor. Which basically means that a new object is created and passed in to the function as this.
prototype is a special object that allows classes to be created and executed. JS doesn't really have classes, like other languages, it has prototypes that provide similar functionality. The prototype object is the same for all instances (objects) of the class, therefore it can be used to share data. In this case, we are using it to share functions. This means that there is only 1 instance of each function, but it is shared by all instances of the class. When you invoke the function (actually called a method now), the specific instance of the class is set as this which allows you to refer to it inside of the function.
createLocations is the name of the function/method that we are creating and it will be stored in the prototype object of the LocationCreator class which is, in turn, stored in the module object.
The function takes in 2 parameters: radius and dst. The radius parameter will be a number and is used to set the size of the sphere that is being created. You will need to make sure that the length of each THREE.Vector3 object is equal to radius. The dst parameter is used to store the points themselves so that they can be used by the calling code.
Everything else is specific to your implementation. You just need to copy the code from your scenario and make it work with the radius and dst parameters.
Now, it seems like you have some variations, since you are based off of EQS which has 3 different sets of angles to generate points from. Have a look at EQS to see how this is handled in that class. Basically, I pass the angles in to the constructor, which stores them as a member variable (this.whatever) so that they can be used in the createLocations function.
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
.
No Joy. Everything works, except EQP.
Thanks for the switch and LocationCreator.prototype.createLocations function explanations.
I believe I've added the three new EQP cases to the createChargePointLocator function() switch properly. When I select an EQP setting on the control panel Precision settings, the output is always the default (Hosohedron.LocationCreator( 4, 2 )).
Over the past two days I tried two things. The first was modifying module var EQP to closely agree with var EQS. Substituting ‘numPoints’ for ‘angles’ and treating the radius variable exactly the same. Creating the value of ‘points’ from the call titles. The objects are a bit different, 'angles' is an array, while the value of numPoints is either 46, 130, or 406. I believe I set the radius to 1 properly, ... .
Next, I commented out most of my first effort, then modified EQP to closely agree with var Hosohedron. That made much more sense. Where Hosohedron receives ( divWidth, divHeight ) from the charge-point-engine precision switch, now EQP.LocationCreator receives the pair of numbers ( radius, points ). While the hoso example is easy to follow; still, no joy seeing an EQP graphic Precision setting yet. I'm afraid that radius may the problem.
I posted all my changes and have run out of guesses. I'll keep looking, but must ask, please give it the once over, find the error and win the prize of your choice.
.
No Joy. Everything works, except EQP.
Thanks for the switch and LocationCreator.prototype.createLocations function explanations.
I believe I've added the three new EQP cases to the createChargePointLocator function() switch properly. When I select an EQP setting on the control panel Precision settings, the output is always the default (Hosohedron.LocationCreator( 4, 2 )).
Over the past two days I tried two things. The first was modifying module var EQP to closely agree with var EQS. Substituting ‘numPoints’ for ‘angles’ and treating the radius variable exactly the same. Creating the value of ‘points’ from the call titles. The objects are a bit different, 'angles' is an array, while the value of numPoints is either 46, 130, or 406. I believe I set the radius to 1 properly, ... .
Next, I commented out most of my first effort, then modified EQP to closely agree with var Hosohedron. That made much more sense. Where Hosohedron receives ( divWidth, divHeight ) from the charge-point-engine precision switch, now EQP.LocationCreator receives the pair of numbers ( radius, points ). While the hoso example is easy to follow; still, no joy seeing an EQP graphic Precision setting yet. I'm afraid that radius may the problem.
I posted all my changes and have run out of guesses. I'll keep looking, but must ask, please give it the once over, find the error and win the prize of your choice.
.
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
Ok, got that working.
There were a few problems. Firstly, the constants used in the switch statement were not defined, so it couldn't match on your case statements and would fall through to the default. That had to happen in the cdm.js file as the module object in charge-point-engine.js is actually the cdm.js module since charge-point-engine is not a module itself, but a module extension (tricky, I know).
Secondly, the EQP class itself had some issues. It was taking the radius in to the constructor, but it shouldn't because the createLocations function of that class already has it passed in as a parameter. That wouldn't stop it from working though, it would just make it ignore the given radius (which it shouldn't do).
The main problem in EQP is that you changed the parameter list for the createLocations function, but then ignored them. You can't change the function declaration on this type of function because it is implementing an interface. An interface is a class that does not provide functionality, but it does provide the functions that will be available in a class that does. It defines the contract for the class. The way it is used. Therefore, we can swap different implementations without changing the code that uses them.
Have a look at the changes in SourceTree and try to see how they fixed it.
There were a few problems. Firstly, the constants used in the switch statement were not defined, so it couldn't match on your case statements and would fall through to the default. That had to happen in the cdm.js file as the module object in charge-point-engine.js is actually the cdm.js module since charge-point-engine is not a module itself, but a module extension (tricky, I know).
Secondly, the EQP class itself had some issues. It was taking the radius in to the constructor, but it shouldn't because the createLocations function of that class already has it passed in as a parameter. That wouldn't stop it from working though, it would just make it ignore the given radius (which it shouldn't do).
The main problem in EQP is that you changed the parameter list for the createLocations function, but then ignored them. You can't change the function declaration on this type of function because it is implementing an interface. An interface is a class that does not provide functionality, but it does provide the functions that will be available in a class that does. It defines the contract for the class. The way it is used. Therefore, we can swap different implementations without changing the code that uses them.
Have a look at the changes in SourceTree and try to see how they fixed it.
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
.
It sure is nice to see it working. I've reviewed each of your corrections and am well able to appreciate them. Especially the fact that the LocationCreator parameter list, ( radius and dst ) is fixed by the class. Where exactly in the charge-point-engine is radius given a value of 1? Module.radius? Whatever that is?
I'll clean up var ECP and the other files of my extraneous commented out code.
Any ideas on how we might compare the performance of EQS versus EQP? Once we have a plan or set of performance measures (optimistic, aren't I), given our previous discussion, I believe I'll need to go through this effort again, making another duplicate of var EQS, call it for var EQS2, for optimizing specific EQS solutions.
Don't forget to claim your prize.
.
It sure is nice to see it working. I've reviewed each of your corrections and am well able to appreciate them. Especially the fact that the LocationCreator parameter list, ( radius and dst ) is fixed by the class. Where exactly in the charge-point-engine is radius given a value of 1? Module.radius? Whatever that is?
I'll clean up var ECP and the other files of my extraneous commented out code.
Any ideas on how we might compare the performance of EQS versus EQP? Once we have a plan or set of performance measures (optimistic, aren't I), given our previous discussion, I believe I'll need to go through this effort again, making another duplicate of var EQS, call it for var EQS2, for optimizing specific EQS solutions.
Don't forget to claim your prize.
.
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
LongtimeAirman wrote:Where exactly in the charge-point-engine is radius given a value of 1? Module.radius? Whatever that is?
In charge-point-engine.js at line 490, it calls the createLocations method with a value for radius of module.RADIUS. That is a constant defined in the current module, so the obvious question is, what is the current module. The charge-point-engine.js file is different because it does not define its own module, but receives one as a parameter and extends it by adding more classes and functions to it. If you look at the top of charge-point-engine.js, after the comment, you will see this:
- Code:
(function( module, THREE, SPHERE, EQS, EQP, Hosohedron )
You can see that module is being passed in as a parameter along with other modules like THREE and our own EQS and EQP modules. So we need to look at what is calling this function, which is actually at the very bottom of the file:
- Code:
}( PIM, THREE, SPHERE, EQS, EQP, Hosohedron ));
The first parameter is PIM, so the module is defined in cdm.js.
LongtimeAirman wrote:Any ideas on how we might compare the performance of EQS versus EQP? Once we have a plan or set of performance measures (optimistic, aren't I), given our previous discussion, I believe I'll need to go through this effort again, making another duplicate of var EQS, call it for var EQS2, for optimizing specific EQS solutions.
I think the best, and easiest, way to compare them is with our eyes. Take pics of both EQS and EQP with the equivalent number of points and from the same camera position. Right now there is no performance difference because EQP is just an offset version of EQS. I think the initial idea was to have every 2nd row be offset, so that it would form a diamond pattern rather than a square like EQS. When that is done, we need to think about how to use the idea of offset rows but incorporate it into the EQS algorithm. Can we create rows between the defined ones and we make them offset, for example. I would actually prefer that we keep the existing EQS rows and leave them alone, but add in more rows to fill in the gaps.
LongtimeAirman wrote:
Don't forget to claim your prize.
Peace and Prosperity for All
or the big teddy bear, which ever is easiest to get off the shelf.
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
.
Our goal is to place N charge sampling points on a sphere of radius 1 as uniformly as possible.
There are currently 4 values for N: 6, 46, 130, 406. The 6 value corresponds to the cardinal directions - up/down, left/right, in/out. The rest were originally Hosohedron solutions ( 4,2; 8,4; 16,8; 32,16 ). The Hosohedron algorithm partitions the sphere’s surface into latitudinal bands similar to the fact that charge emission is a function of the particle’s latitude. It became clear that the hosohedrons were wrong. The point distribution isn’t uniform, it is highest near the poles. This fact was made apparent by our scenarios.
Aside from ( 4,2 ) the other three Hosohedron solutions were replaced with equi-latitude area EQS algorithm solutions. I‘ve shown that I can improve EQS solutions with offsetting alternate latitude rows.
My next step is to identify a methodology to improve the EQS particle distribution uniformity. For example, beginning with EQS46, using a spherical scenario, I’ll find an approximate smallest spherical configuration radius that 46 r=1 particles can fit without any particle contact. Then I’ll try my alternate row offset adjustments to see if I can fit in any additional particles without any resulting particle contact. I'll attempt the same with EQS high and overdrive. We can decide how best to make those modifications after I use autocad to identify them.
Next, we'd compare the optimized EQS solutions to EQP. Like you, I believe EQP provides a more uniform set of points than EQS does, but we haven’t really determined that yet, including what is the smallest radius spherical configurations with the same total number of r=1 particles.
I'm keeping the same (or approximate ) N values - they might be changed slightly to maximize any advantage offered by the EQS or EQP solutions.
S'alright?
.
I agree, that suits me. But I don't believe we're ready to compare EQS and EQP yet.I think the best, and easiest, way to compare them is with our eyes. Take pics of both EQS and EQP with the equivalent number of points and from the same camera position.
I disagree or don’t understand. EQP is an alternative algorithm, not just an offset version of EQS.Right now there is no performance difference because EQP is just an offset version of EQS.
Here's my summary and plan.I think the initial idea was to have every 2nd row be offset, so that it would form a diamond pattern rather than a square like EQS. When that is done, we need to think about how to use the idea of offset rows but incorporate it into the EQS algorithm. Can we create rows between the defined ones and we make them offset, for example. I would actually prefer that we keep the existing EQS rows and leave them alone, but add in more rows to fill in the gaps.
Our goal is to place N charge sampling points on a sphere of radius 1 as uniformly as possible.
There are currently 4 values for N: 6, 46, 130, 406. The 6 value corresponds to the cardinal directions - up/down, left/right, in/out. The rest were originally Hosohedron solutions ( 4,2; 8,4; 16,8; 32,16 ). The Hosohedron algorithm partitions the sphere’s surface into latitudinal bands similar to the fact that charge emission is a function of the particle’s latitude. It became clear that the hosohedrons were wrong. The point distribution isn’t uniform, it is highest near the poles. This fact was made apparent by our scenarios.
Aside from ( 4,2 ) the other three Hosohedron solutions were replaced with equi-latitude area EQS algorithm solutions. I‘ve shown that I can improve EQS solutions with offsetting alternate latitude rows.
My next step is to identify a methodology to improve the EQS particle distribution uniformity. For example, beginning with EQS46, using a spherical scenario, I’ll find an approximate smallest spherical configuration radius that 46 r=1 particles can fit without any particle contact. Then I’ll try my alternate row offset adjustments to see if I can fit in any additional particles without any resulting particle contact. I'll attempt the same with EQS high and overdrive. We can decide how best to make those modifications after I use autocad to identify them.
Next, we'd compare the optimized EQS solutions to EQP. Like you, I believe EQP provides a more uniform set of points than EQS does, but we haven’t really determined that yet, including what is the smallest radius spherical configurations with the same total number of r=1 particles.
I'm keeping the same (or approximate ) N values - they might be changed slightly to maximize any advantage offered by the EQS or EQP solutions.
S'alright?
.
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
I switched between EQS and EQP and it just looks like EQP is slightly rotated around the equator compared to EQS. I might be wrong and am happy to see any evidence of it.
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
.
I'll share my meager progress.
Jump right into overdrive. EQS406. With r=1 particles, the minimum spherical radius - without particle contact, is just under 14. At that distance, the r=1 particles are 8.35 angular degrees. Contact occurs between the 3 and the nine particle ring latitudes. Using equatorial offsets, we can add an equator and a new latitude ring. The original 8 equatorial latitude rings, (with 30,30,36,36,36,36,30,30 particles) separated by about 10 degrees have been replaced with 11 latitude rings (of 30 particles each) separated by 7.1916 degrees. N increased from 406 to 472. Not shown. That number could be increased further by addressing the pole latitudes, but I don’t see the point pushing past overdrive – that’s supposed to be our limit. It makes sense to start with a smaller EQS solution, with two less latitude rows compared with 406, then optimize that solution to replace the existing EQS406.
With that in mind I’ll begin with EQS372 northern hemisphere latitudes (up from the equator at zero) and particle ring counts.
[ 11.25, 12 ], // 30 particles
[ 22.5, 12 ], // 30 "
[ 33.75, 12 ], // 30 "
[ 45, 17.1429 ], // 21 "
[ 56.25, 20 ], // 18 "
[ 67.5, 24 ], // 15 "
[ 78.75, 40 ], // 9 "
[ 88.5, 120 ] // 3 "

Working the Overdrive EQS optimization.
Using equatorial offsets, of 360/30/2 degrees, I added a new 30 particle equatorial ring which bumped the EQS372 up to a modEQS402. With r=1 particles, the minimum spherical particle configuration radius - without particle contact, for the 372 (and 402) is just under 12, two smaller than the 406 radius, so the particles appear larger in the modEQS402 image.
I see the 402 is a good improvement in particle uniformity over the EQS406. I'll work the pole ends next, beginning with rotating the 3 particle pole rings by 20 degrees about the pole-to-pole axis. I'll move and may even might add a new polar latitude as well. All changes are straightforward. The particle count should increase a little bit more.
I'll be busy offline for the next two days.
.
I'll share my meager progress.
Jump right into overdrive. EQS406. With r=1 particles, the minimum spherical radius - without particle contact, is just under 14. At that distance, the r=1 particles are 8.35 angular degrees. Contact occurs between the 3 and the nine particle ring latitudes. Using equatorial offsets, we can add an equator and a new latitude ring. The original 8 equatorial latitude rings, (with 30,30,36,36,36,36,30,30 particles) separated by about 10 degrees have been replaced with 11 latitude rings (of 30 particles each) separated by 7.1916 degrees. N increased from 406 to 472. Not shown. That number could be increased further by addressing the pole latitudes, but I don’t see the point pushing past overdrive – that’s supposed to be our limit. It makes sense to start with a smaller EQS solution, with two less latitude rows compared with 406, then optimize that solution to replace the existing EQS406.
With that in mind I’ll begin with EQS372 northern hemisphere latitudes (up from the equator at zero) and particle ring counts.
[ 11.25, 12 ], // 30 particles
[ 22.5, 12 ], // 30 "
[ 33.75, 12 ], // 30 "
[ 45, 17.1429 ], // 21 "
[ 56.25, 20 ], // 18 "
[ 67.5, 24 ], // 15 "
[ 78.75, 40 ], // 9 "
[ 88.5, 120 ] // 3 "

Working the Overdrive EQS optimization.
Using equatorial offsets, of 360/30/2 degrees, I added a new 30 particle equatorial ring which bumped the EQS372 up to a modEQS402. With r=1 particles, the minimum spherical particle configuration radius - without particle contact, for the 372 (and 402) is just under 12, two smaller than the 406 radius, so the particles appear larger in the modEQS402 image.
I see the 402 is a good improvement in particle uniformity over the EQS406. I'll work the pole ends next, beginning with rotating the 3 particle pole rings by 20 degrees about the pole-to-pole axis. I'll move and may even might add a new polar latitude as well. All changes are straightforward. The particle count should increase a little bit more.
I'll be busy offline for the next two days.
.
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
.
EQS406 versus modEQS372.
Our simulated charge field particles react to the ambient charge field according to the ‘charge’ received at their charge sampling points. Those points are currently calculated by an equi-iso-latitudinal area algorithm called EQS. We currently use three EQS solutions - 46, 130 and 406.
Any algorithm has its purpose and limitations. We may improve the behavior of our charge field particles by increasing the uniformity of the sample point distribution sets over our current EQS precision ‘standards’ by careful modifications. We can conveniently display those sampling point distribution sets by placing neutral particles in the ‘same’ spherical configurations for easy review. These mods may indicate simple improvements to the algorithm itself.

EQS406 compared to EQS 342 modified into modEQS372.
Please reference the above image. In my last post I showed the ‘Overdrive’ spherical configuration - EQS406 and possible alternative configuration, modEQS402 still needing some pole optimization. That pole mod led me to begin at a different EQS solution, modifying EQS342 into a modEQS372, currently my recommended replacement for EQS406.
As in my previous post, with r=1 particles, the minimum spherical particle configuration radius without particle contact, for the EQS342 (and modEQS372) is just under 12. The ‘minimum’ EQS406 radius without particle contact is 14. The EQS406 has 9 northern hemisphere latitude particle rings separated by about 10 degrees: (3, 9, 15, 20, 24, 30, 30, 36, 36). That same set is repeated in the southern hemisphere.
Starting with EQS342 - (3, 9, 15, 18, 21, 30, 30, 30, 30, 30, 30, 21, 18, 15, 9, 3). Sixteen latitude rings, totaling 342 points. Make the following modifications:
1. Adding single particles over the poles. EQS doesn’t provide single pole particles. [ 90, 360 ] results in a particle that ‘leans’ on the p-to-p axis.
2. Offsetting adjacent pole latitude rings. EQS partitions the spherical surface in both latitude and longitudinal alignments. Instead of the current six minimum gaps; point the hex between 2 of the 12 particles in the next particle ring instead of directly at six of them by rotating the 6 particle ring latitude 360/12/2 or 15 degrees. If the pole was three point, it would need the same rotation with respect to its neighboring latitude. Pole latitudes numbers that aren't evenly divisible may not benifit from offset rotations. Note, the modEQS372 in the image still needs its hex rotation. EQS342’s polar latitude group: 3, 9, 15, 18, 21 was changed to modEQS372’s 1, 6, 12, 18, 21, 24.
3. Offsetting adjacent equatorial latitude rings. Given rows of equal number (30) particle rings, we can increase the distance between adjacent (elevation) particles by alternating the starting positions of the each particle ring 360/30/2, 6 degrees. Offsetting adjacent latitudes allows us to change reduce the elevation angle of adjacent latitudes results the resulting distinctive hexagonal alignments.
4. Adding a new 30 particle ring over the equator. Note, all EQS algorithm solutions lack equatorial rings. Offsetting the equatorial latitudes has allowed us to replace the previous 6 latitudes with 10 degree separation to 7 latitudes, each separated by 8.7 degrees, with resulting distinctive hexagonal alignments.
The result is modEQS372 - (1, 6, 12, 18, 21, 24, 30, 30, 30, 30, 30, 30, 30, 24, 21, 18, 12, 6, 1). 19 latitudes with 372 points. The modifications above result in increased numbers of particles at EQS342’s radius of 12, without allowing r=1 particles to overlap; EQS406’s minimum radius without r=1 particle overlap is 14.
The new modified distribution is densest between adjacent (azimuthal) particles within the two +/-30 particle ring latitudes at the shoulders. The ‘density’ of points reduces toward both the equator and poles.
The main limitation of this method is maximizing the number of equal particle ring latitudes. I believe there are just a small set of two modifiable EQS solutions at this ‘scale’, involving only those solutions with 4 or 6 equal particle length equatorial latitudes. ModEQS372 handles the 6 case, six equatorial latitudes become the modified seven. The EQS130 competition will handle the other, by changing an EQS solution with 4 adjacent (elevation) equal particle equatorial latitudes into the modified five.
EQS130 contenders next.
.
EQS406 versus modEQS372.
Our simulated charge field particles react to the ambient charge field according to the ‘charge’ received at their charge sampling points. Those points are currently calculated by an equi-iso-latitudinal area algorithm called EQS. We currently use three EQS solutions - 46, 130 and 406.
Any algorithm has its purpose and limitations. We may improve the behavior of our charge field particles by increasing the uniformity of the sample point distribution sets over our current EQS precision ‘standards’ by careful modifications. We can conveniently display those sampling point distribution sets by placing neutral particles in the ‘same’ spherical configurations for easy review. These mods may indicate simple improvements to the algorithm itself.

EQS406 compared to EQS 342 modified into modEQS372.
Please reference the above image. In my last post I showed the ‘Overdrive’ spherical configuration - EQS406 and possible alternative configuration, modEQS402 still needing some pole optimization. That pole mod led me to begin at a different EQS solution, modifying EQS342 into a modEQS372, currently my recommended replacement for EQS406.
As in my previous post, with r=1 particles, the minimum spherical particle configuration radius without particle contact, for the EQS342 (and modEQS372) is just under 12. The ‘minimum’ EQS406 radius without particle contact is 14. The EQS406 has 9 northern hemisphere latitude particle rings separated by about 10 degrees: (3, 9, 15, 20, 24, 30, 30, 36, 36). That same set is repeated in the southern hemisphere.
Starting with EQS342 - (3, 9, 15, 18, 21, 30, 30, 30, 30, 30, 30, 21, 18, 15, 9, 3). Sixteen latitude rings, totaling 342 points. Make the following modifications:
1. Adding single particles over the poles. EQS doesn’t provide single pole particles. [ 90, 360 ] results in a particle that ‘leans’ on the p-to-p axis.
2. Offsetting adjacent pole latitude rings. EQS partitions the spherical surface in both latitude and longitudinal alignments. Instead of the current six minimum gaps; point the hex between 2 of the 12 particles in the next particle ring instead of directly at six of them by rotating the 6 particle ring latitude 360/12/2 or 15 degrees. If the pole was three point, it would need the same rotation with respect to its neighboring latitude. Pole latitudes numbers that aren't evenly divisible may not benifit from offset rotations. Note, the modEQS372 in the image still needs its hex rotation. EQS342’s polar latitude group: 3, 9, 15, 18, 21 was changed to modEQS372’s 1, 6, 12, 18, 21, 24.
3. Offsetting adjacent equatorial latitude rings. Given rows of equal number (30) particle rings, we can increase the distance between adjacent (elevation) particles by alternating the starting positions of the each particle ring 360/30/2, 6 degrees. Offsetting adjacent latitudes allows us to change reduce the elevation angle of adjacent latitudes results the resulting distinctive hexagonal alignments.
4. Adding a new 30 particle ring over the equator. Note, all EQS algorithm solutions lack equatorial rings. Offsetting the equatorial latitudes has allowed us to replace the previous 6 latitudes with 10 degree separation to 7 latitudes, each separated by 8.7 degrees, with resulting distinctive hexagonal alignments.
The result is modEQS372 - (1, 6, 12, 18, 21, 24, 30, 30, 30, 30, 30, 30, 30, 24, 21, 18, 12, 6, 1). 19 latitudes with 372 points. The modifications above result in increased numbers of particles at EQS342’s radius of 12, without allowing r=1 particles to overlap; EQS406’s minimum radius without r=1 particle overlap is 14.
The new modified distribution is densest between adjacent (azimuthal) particles within the two +/-30 particle ring latitudes at the shoulders. The ‘density’ of points reduces toward both the equator and poles.
The main limitation of this method is maximizing the number of equal particle ring latitudes. I believe there are just a small set of two modifiable EQS solutions at this ‘scale’, involving only those solutions with 4 or 6 equal particle length equatorial latitudes. ModEQS372 handles the 6 case, six equatorial latitudes become the modified seven. The EQS130 competition will handle the other, by changing an EQS solution with 4 adjacent (elevation) equal particle equatorial latitudes into the modified five.
EQS130 contenders next.
.
Last edited by LongtimeAirman on Thu Feb 21, 2019 7:00 pm; edited 1 time in total (Reason for editing : Typos!)
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
.

EQS130, along with two alternatives, modEQS128 and modEQS144 are shown. A few small changes to the existing EQS algorithm (ex. EQS 130) result in the two modified and, I believe, improved (equidistant) point distributions - as shown.
You have my sympathies, post after post of particles in spherical configurations. This is a working project and the devil’s in the details. As you no doubt already know (too well), the present goal is to improve the uniformity of distribution (equi-distance wise) of our calculated particle’s charge field sampling points. That should have the side benefit of improved overall performance of our possible charged particle field simulation engine.
Note that the engine is being used as a tool to model the sampling points of a single particle as particle configurations. Aside from my autocad modifications, our particle engine allows one to make these models. I consider them as real and valid in some sense, although to be perfectly honest, I cannot explain nor justify the validity of spherical particle configurations with respect to the charge field. Nevertheless, I’ll work toward developing a spherical group UI that will allow a casual user to create many of them herself. Then that single spherical UI scenario could allow me to discard several redundant and tool scenarios currently in the Spherical group.
The user just selects from these precision levels: Low, Med, High and Overdrive. The default is low. I discussed Overdrive in my last post. EQS130 is our simulation’s high Precision standard, made up of (3, 9, 15, 18, 20, 20, 18, 15, 9, 3), 10 particle ring latitudes totaling 130 particles, and is shown in the top row of the image. This configuration begins to overlap the r=1 particles at about R=7.1. R=7.5 in the EQS130 first row of images.
ModEQS128. – (1, 6, 12, 18, 18, 18, 18, 18, 12, 6, 1), 11 rings, 128 particles. The first alternative to ECP130 begins with EQS108 – (6, 12, 18, 18, 18, 18, 12, 6), 10 particle ring latitudes totaling 108 particles. The configuration begins to overlap the r=1 surface particles near R=6.6. R=7 in the EQS108, as well as the modEQS128– second row images. The modifications are as follows:
1. Add single pole particles.
2. Rotate the 6 particle ring pole, 360/12/2 = 15 degrees. This allows slightly more room between the 6 and 12 particle ring latitudes – say for a slightly larger 6, or smaller 12 particle rings.
3. Convert the four equatorial 18 particle rings into five by adding a new 18 particle ring and
4. Offsetting, or alternating the starting point of each adjacent 18 particle latitude ring by 360/18/2 = 10 degrees (az) so that the 5 rows will form a hexagonal pattern.
ModEQS144 – (3, 9, 15, 18, 18, 18, 18, 18, 15, 9, 3), 11 rings, 144 particles. It is also shown (third row) at the configuration radius R=7. It began as EQS126 (3, 9, 15, 18, 18, 18, 18, 15, 9, 3). Here are the 144 modifications:
1. Rotate the pole triangles 360/9/2 = 20 degrees (az).
2. Offset equal particle (18) equatorial latitudes 360/18/2 = 10 degrees, thereby making room to;
3. Add a new 18 particle latitude ring, increasing the number equatorial latitudes from 4 to 5 in the same area.
I believe both the ModEQS128 and ModEQS144 alternatives provide more uniform point distributions then EQS130.
I’ll look at EQS46, the Medium Precision, next.
.

EQS130, along with two alternatives, modEQS128 and modEQS144 are shown. A few small changes to the existing EQS algorithm (ex. EQS 130) result in the two modified and, I believe, improved (equidistant) point distributions - as shown.
You have my sympathies, post after post of particles in spherical configurations. This is a working project and the devil’s in the details. As you no doubt already know (too well), the present goal is to improve the uniformity of distribution (equi-distance wise) of our calculated particle’s charge field sampling points. That should have the side benefit of improved overall performance of our possible charged particle field simulation engine.
Note that the engine is being used as a tool to model the sampling points of a single particle as particle configurations. Aside from my autocad modifications, our particle engine allows one to make these models. I consider them as real and valid in some sense, although to be perfectly honest, I cannot explain nor justify the validity of spherical particle configurations with respect to the charge field. Nevertheless, I’ll work toward developing a spherical group UI that will allow a casual user to create many of them herself. Then that single spherical UI scenario could allow me to discard several redundant and tool scenarios currently in the Spherical group.
The user just selects from these precision levels: Low, Med, High and Overdrive. The default is low. I discussed Overdrive in my last post. EQS130 is our simulation’s high Precision standard, made up of (3, 9, 15, 18, 20, 20, 18, 15, 9, 3), 10 particle ring latitudes totaling 130 particles, and is shown in the top row of the image. This configuration begins to overlap the r=1 particles at about R=7.1. R=7.5 in the EQS130 first row of images.
ModEQS128. – (1, 6, 12, 18, 18, 18, 18, 18, 12, 6, 1), 11 rings, 128 particles. The first alternative to ECP130 begins with EQS108 – (6, 12, 18, 18, 18, 18, 12, 6), 10 particle ring latitudes totaling 108 particles. The configuration begins to overlap the r=1 surface particles near R=6.6. R=7 in the EQS108, as well as the modEQS128– second row images. The modifications are as follows:
1. Add single pole particles.
2. Rotate the 6 particle ring pole, 360/12/2 = 15 degrees. This allows slightly more room between the 6 and 12 particle ring latitudes – say for a slightly larger 6, or smaller 12 particle rings.
3. Convert the four equatorial 18 particle rings into five by adding a new 18 particle ring and
4. Offsetting, or alternating the starting point of each adjacent 18 particle latitude ring by 360/18/2 = 10 degrees (az) so that the 5 rows will form a hexagonal pattern.
ModEQS144 – (3, 9, 15, 18, 18, 18, 18, 18, 15, 9, 3), 11 rings, 144 particles. It is also shown (third row) at the configuration radius R=7. It began as EQS126 (3, 9, 15, 18, 18, 18, 18, 15, 9, 3). Here are the 144 modifications:
1. Rotate the pole triangles 360/9/2 = 20 degrees (az).
2. Offset equal particle (18) equatorial latitudes 360/18/2 = 10 degrees, thereby making room to;
3. Add a new 18 particle latitude ring, increasing the number equatorial latitudes from 4 to 5 in the same area.
I believe both the ModEQS128 and ModEQS144 alternatives provide more uniform point distributions then EQS130.
I’ll look at EQS46, the Medium Precision, next.
.
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
.
I don’t see how the methodology I’ve been using can “optimize” the EQS46. I suppose I could come up with an objective quantitative measure of equi-spaced points in order to evaluate the EQS46, and then compare it to an alternative, there are many standard polyhedral forms to choose from. I also wanted to give an additional look at the geodesics. Also I’m sure the ‘fullerene’ icosa-based carbon configuration, C60 would be better choice than the EQS46.
Here’s another idea I’ve picked up in my readings, that I need to pass by you. Particle placements based on repulsion; our possible charged particle field should be able to handle that. Using the EQP algorithm, an arbitrary number of Protons can be positioned at the spherical configuration’s radius with their south poles oriented toward the spherical configuration’s center. I imagine the protons’ emission fields may then push each proton into optimal positions which we may then use as an ideal Precision solution set for that number of points.
In order to do that, we must constrain the protons’ motions to the spherical radius. Specifically, is it possible - relatively easily – to: 1. Immobilize, fix, or make Unmoveable - both the proton’s spin axis to always point to the configuration center; as well as 2. Fix the protons distance from that center?
Optimistic, eh? I had to ask.
.
I don’t see how the methodology I’ve been using can “optimize” the EQS46. I suppose I could come up with an objective quantitative measure of equi-spaced points in order to evaluate the EQS46, and then compare it to an alternative, there are many standard polyhedral forms to choose from. I also wanted to give an additional look at the geodesics. Also I’m sure the ‘fullerene’ icosa-based carbon configuration, C60 would be better choice than the EQS46.
Here’s another idea I’ve picked up in my readings, that I need to pass by you. Particle placements based on repulsion; our possible charged particle field should be able to handle that. Using the EQP algorithm, an arbitrary number of Protons can be positioned at the spherical configuration’s radius with their south poles oriented toward the spherical configuration’s center. I imagine the protons’ emission fields may then push each proton into optimal positions which we may then use as an ideal Precision solution set for that number of points.
In order to do that, we must constrain the protons’ motions to the spherical radius. Specifically, is it possible - relatively easily – to: 1. Immobilize, fix, or make Unmoveable - both the proton’s spin axis to always point to the configuration center; as well as 2. Fix the protons distance from that center?
Optimistic, eh? I had to ask.
.
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
Yes, those things are possible, but it isn't pretty and breaks the model we are trying to create. It would require a custom model. I don't think it is worth the effort. It also won't work because the emission gives the particles a velocity which doesn't stop when it reaches some optimal position. They will just keep going (you could step through it, frame by frame to fix this). Plus, how are you going to place them at the start? Wouldn't that placement choose the final positions, with slight variations given that the protons emission is not spherical? That emission profile is a problem too. We don't want it to be a factor is choosing charge reception, only emission.
In order to test the charge point configurations, we can use a bit of math. There is probably some better way to do it, but when I'm in unknown territory and can't see a nice solution, I tend to brute force it and then look for optimizations later.
We take each generated charge point and we calculate the distance to all other particles. We then find the minimum value from that set. So we end up with a minimum value per charge point. Then we compare all of the minimum values to each other. There are many ways to do that but just putting them into a graph would be a good start. If you end up with a straight horizontal line, then you have found an optimal solution. The most optimal solution is that which is closest to Y=0 on the graph.
In order to test the charge point configurations, we can use a bit of math. There is probably some better way to do it, but when I'm in unknown territory and can't see a nice solution, I tend to brute force it and then look for optimizations later.
We take each generated charge point and we calculate the distance to all other particles. We then find the minimum value from that set. So we end up with a minimum value per charge point. Then we compare all of the minimum values to each other. There are many ways to do that but just putting them into a graph would be a good start. If you end up with a straight horizontal line, then you have found an optimal solution. The most optimal solution is that which is closest to Y=0 on the graph.
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
.
With respect to points on a sphere, I believe repulsion is actually an iterative process. Based on increasing the distance between the closest points in the set of N points on a sphere at a given iteration. It’s another possible alternative to our current EQS and EQP algorithms I hadn’t gotten into - there are many. Equi-distant points on a sphere aren't true beyond the platonic solids, and are only approximated. I thought if we had ‘real proton repulsion’ - given an EQP starting set – it might work; but you’re correct, I ‘overlooked’ the constant motion of the non-zero velocities as the protons keep repelling each other.
I should point out my obvious thinking. Fixing orientations and distances in the way I suggested mimics the coherence orientation. I suppose any coherence in our possible charged particle field would also require a custom model.
With that in mind, and not for the first time, I googled something like “equi-spacing points on a sphere”, and found an algorithm based on s-curves on the sphere. It’s undergraduate, easy to read for anyone interested in the subject. Nice looking results and it also includes an efficiency function that sounds like what you had in mind.
A New Computationally Efficient Method for Spacing n Points on a Sphere Jonathan Kogan https://scholar.rose-hulman.edu/rhumj/vol18/iss2/5/
Pages 54 – 71.
Also, the results look good. The Mathematica code is included, here's the Python code.
Airman. Ok, nix the repulsion idea.Nevyn wrote: Yes, those things are possible, but it isn't pretty and breaks the model we are trying to create. … .
With respect to points on a sphere, I believe repulsion is actually an iterative process. Based on increasing the distance between the closest points in the set of N points on a sphere at a given iteration. It’s another possible alternative to our current EQS and EQP algorithms I hadn’t gotten into - there are many. Equi-distant points on a sphere aren't true beyond the platonic solids, and are only approximated. I thought if we had ‘real proton repulsion’ - given an EQP starting set – it might work; but you’re correct, I ‘overlooked’ the constant motion of the non-zero velocities as the protons keep repelling each other.
I should point out my obvious thinking. Fixing orientations and distances in the way I suggested mimics the coherence orientation. I suppose any coherence in our possible charged particle field would also require a custom model.
I take it you would like to see some quantitative measure in support of selecting alternative precision candidates, suggesting “brute force” for a start. That’s a change, up to now, I’ve been relying on images to compare the precision candidates, I’ll shoot for numbers too.Nevyn wrote: In order to test the charge point configurations. ...
We take each generated charge point and we calculate the distance to all other particles. …
With that in mind, and not for the first time, I googled something like “equi-spacing points on a sphere”, and found an algorithm based on s-curves on the sphere. It’s undergraduate, easy to read for anyone interested in the subject. Nice looking results and it also includes an efficiency function that sounds like what you had in mind.
A New Computationally Efficient Method for Spacing n Points on a Sphere Jonathan Kogan https://scholar.rose-hulman.edu/rhumj/vol18/iss2/5/
Pages 54 – 71.
Pg 62. … we first created three new functions to analyze how well the points were spaced on a sphere: SmallestDistance, TheoreticalSmallestDistance, and NormalizedSmallestDistance.
SmallestDistance(pts) takes a list of points and identifies the smallest Euclidean distance between any two points on the sphere. In other words, it identifies the two points that are closest together and outputs the distance between the two.
The TheoreticalSmallestDistance(n) function returns the upper bound for the distance of n equally spaced points on a sphere. It is well known that the optimal spacing of points on the plane is the hexagonal grid. To find the upper bound for the distance of n points on a sphere, we imagine there is a planar hexagonal grid that covers the entire area of the sphere. Using this grid, we find this upper bound for all n values based on the size and the number of equilateral triangles.
Lastly, we defined the NormalizedSmallestDistance(pts) function as the SmallestDistance(pts)/TheoreticalSmallestDistance(Length(pts)); the function provides a relative accuracy for the points that are around the sphere.
Also, the results look good. The Mathematica code is included, here's the Python code.
Pg 70. The research discussed in this paper has also led to the creation of the Mathematica function SpherePoints[n], which was added in the Mathematica 11.1 update [10]. This Mathematica function enables anybody who wants points spaced equally on a sphere to generate them quickly and easily [8].
- Code:
Pg 72. A.2 Python Code
import math
def spherical coordinate (x , y ):
return [math. cos (x) ∗ math. cos (y) ,
math. sin (x) ∗ math. cos (y) , math. sin (y )]
def NX(n, x ):
pts =[]
start = (−1. + 1. / (n − 1.))
increment = (2. − 2. / (n − 1.)) / (n − 1.)
for j in xrange(0 , n):
s = start + j ∗ increment
pts . append(
spherical coordinate (
s ∗ x , math. pi / 2. ∗
math. copysign (1 , s ) ∗
(1. − math. sqrt (1. − abs( s )))
))
return pts
def generate points (n):
return NX(n, 0.1 + 1.2 ∗ n)
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
.
Status update. Unfortunately, Jonathan Kogan’s paper didn’t provide all the details. The program is more complicated than it first appeared, and I haven’t decided how I should go about re-organizing the code I previously posted. The important thing is supposed to be the “efficiency measure”. Requoting TheoreticalSmallestDistance(n), “we imagine there is a planar hexagonal grid that covers the entire area of the sphere”, that’s all the information provided on that subject.
I decided to go through the exercise of figuring out the efficiency measure while adding a simpler type of spiral algorithm, based on the Golden ratio. From, Evenly distributed points on sphere,
https://web.archive.org/web/20060728050730/http://cgafaq.info/wiki/Evenly_Distributed_Points_On_Sphere. Also Points on a sphere, October 4th, 2006 by Patrick Boucher. //http://www.softimageblog.com/archives/115
In the meantime, I found Jonathan Kogan’s youtube video of his paper, A New Computationally Efficient Method for Spacing n Points on a Sphere
.
The Efficiency measure, including the TheoreticalSmallestDistance(n) equation I was searching for appears to be part of a small set (3 or 4(?)) of slides – not included in the paper - that served for brief glimpses in the two videos, good enough for a screen capture.

Outputs for the new Golden ratio spherical algorithm with Efficiency measure are shown. Above, the spherical configuration GS50 is on the left and GS406 (from the inside) is on the right. We are looking down along the main N/S y axis for both. While the overall spacing is nice, the poles are either clumped or open.
The Efficiency Measure for GS406 is shown below. Assuming I implemented it correctly the normalized efficiency measure is a poor 0.674. According to Kogan’s paper the best efficiences are about 0.85. Radius 16 is cutting it close, the two closest r=1 neutrons are separated by just 0.040 – almost touching. If one were interested in the just the efficiency numbers, it’s easy to switch between the Parameters and Output control tabs. Curious to see the results, beginning with 10, and incrementing by five up to 65, then 130, then 406, the best efficiency I found was 0.7115 for 10 neutrons, with a fairly straight line dropping to the the GS406’s 0.674. The Golden ratio I implemented is not a good source for equi-distant spaced points necessary for our desired charge detection Precision candidates.

.
Status update. Unfortunately, Jonathan Kogan’s paper didn’t provide all the details. The program is more complicated than it first appeared, and I haven’t decided how I should go about re-organizing the code I previously posted. The important thing is supposed to be the “efficiency measure”. Requoting TheoreticalSmallestDistance(n), “we imagine there is a planar hexagonal grid that covers the entire area of the sphere”, that’s all the information provided on that subject.
I decided to go through the exercise of figuring out the efficiency measure while adding a simpler type of spiral algorithm, based on the Golden ratio. From, Evenly distributed points on sphere,
https://web.archive.org/web/20060728050730/http://cgafaq.info/wiki/Evenly_Distributed_Points_On_Sphere. Also Points on a sphere, October 4th, 2006 by Patrick Boucher. //http://www.softimageblog.com/archives/115
- Code:
inc := pi*(3-sqrt(5))
off := 1/(2*N) - 1
for k := 0 .. N-1
z := k/N + off
r := sqrt(1-z*z)
phi := k*inc
pt[k] := (cos(phi)*r, sin(phi)*r, z)
In the meantime, I found Jonathan Kogan’s youtube video of his paper, A New Computationally Efficient Method for Spacing n Points on a Sphere
.
The Efficiency measure, including the TheoreticalSmallestDistance(n) equation I was searching for appears to be part of a small set (3 or 4(?)) of slides – not included in the paper - that served for brief glimpses in the two videos, good enough for a screen capture.
- Code:
smallestDistance[pts_] := min[table[N[euclideanDistance[pts[[i]], pts[[j]]]],{i,1.0, length[pts]}, {j, i + 1.0, length[pts]}]]
theorecticalSmallestDistance[pts_] := Math.sqrt(8*Math.PI/(n*Math.sqrt(3)))
normalizedSmallestDistance[pts_]:= smallestDistance[pts]/theorecticalsmallestDistance[length[pts_]]

Outputs for the new Golden ratio spherical algorithm with Efficiency measure are shown. Above, the spherical configuration GS50 is on the left and GS406 (from the inside) is on the right. We are looking down along the main N/S y axis for both. While the overall spacing is nice, the poles are either clumped or open.
The Efficiency Measure for GS406 is shown below. Assuming I implemented it correctly the normalized efficiency measure is a poor 0.674. According to Kogan’s paper the best efficiences are about 0.85. Radius 16 is cutting it close, the two closest r=1 neutrons are separated by just 0.040 – almost touching. If one were interested in the just the efficiency numbers, it’s easy to switch between the Parameters and Output control tabs. Curious to see the results, beginning with 10, and incrementing by five up to 65, then 130, then 406, the best efficiency I found was 0.7115 for 10 neutrons, with a fairly straight line dropping to the the GS406’s 0.674. The Golden ratio I implemented is not a good source for equi-distant spaced points necessary for our desired charge detection Precision candidates.

.
Last edited by LongtimeAirman on Fri Mar 15, 2019 7:05 pm; edited 1 time in total (Reason for editing : Added efficiency code)
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
.

Kogan spiral algorithm, 201 r=1 Neutrons, the configuration radius is 25.
The Kogan spiral algorithm and efficiency measure has been added to the spherical scenarios. Now that we have pictures as well as numbers we can make actual qualitative comparisons. Here’s an abbreviated efficiency calculation - Smallest/Theoretical - for the current three EQS precision standards versus EQP, Golden and Kogan algorithm results.

EQP with 404 particles at 0.797 is higher - better point distribution efficiency - than EQS 406 at 0.788 and Kogan 406 at 0.789.
Next, if I continue as planned, I should look at modifying EQS results by adding an equatorial row of particles and rotating alternate latitudes which could improve the current EQS standard. Also, as I mentioned previously, I should be getting better Golden results. I need to look into that too.
.

Kogan spiral algorithm, 201 r=1 Neutrons, the configuration radius is 25.
The Kogan spiral algorithm and efficiency measure has been added to the spherical scenarios. Now that we have pictures as well as numbers we can make actual qualitative comparisons. Here’s an abbreviated efficiency calculation - Smallest/Theoretical - for the current three EQS precision standards versus EQP, Golden and Kogan algorithm results.

EQP with 404 particles at 0.797 is higher - better point distribution efficiency - than EQS 406 at 0.788 and Kogan 406 at 0.789.
Next, if I continue as planned, I should look at modifying EQS results by adding an equatorial row of particles and rotating alternate latitudes which could improve the current EQS standard. Also, as I mentioned previously, I should be getting better Golden results. I need to look into that too.
.
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
.
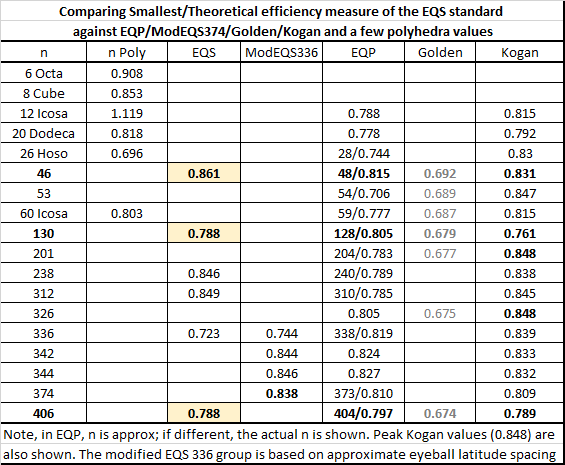
Well Sir, great pain and joy, another fine possible charge particle engine programming tasking is tentatively complete, an efficiency measure is now included with most all our point configurations. Assuming it’s correct, the expanded efficiency table above shows the results.
The polyhedral vertex set – octahedron, cube, icosahedron and pentagonal dodecahedron surprised me. I had assumed the platonic solids were the only ideal solutions. The equidistant spacing of the vertices of the octahedron are the most ideal on the board - 0.908 - closest to one. What does the icosa’s greater than one value, 1.119 mean? Mediocre cube and dodeca values. I can see why the hoso’s are extinct.
The EQS precision set: 46, 130 and 406 are bold and highlighted. EQS238-0.846, and EQS312 – 0.849, would make better standards than EQS 130 and 406. I apologize for giving you grief over the rectangular plot algorithm which you converted to centroids. Given it’s overall values, I have a greater respect for the EQS algorithm and your implementation of it.

I claimed I could improve the efficiencies of some EQS solutions by adding an equatorial particle ring, or pole particles, rotating alternate equatorial or polar latitude rings, so I created a new spherical group scenario “EQS Mods” that shows such mods to EQS336: The result is a very respectable Mod EQS374 with efficiency value of 0.838. I didn’t quite follow the ‘dw centroids logic’ so I adjusted the latitudes by eye, trial and error. I need to work this with autocad and see if I can improve that number further.
Once again, the Golden algorithm has a poor and very linear efficiency result – it must be wrong. On the other hand, the new Kogan algorithm is as good as Golden. K201 or K326 would make fine standards.
The primary benefit of this table is that it provides sufficient justification in selecting a more efficient short list of precision alternatives.
Any thoughts? Feedback? Additional taskings?
.

Well Sir, great pain and joy, another fine possible charge particle engine programming tasking is tentatively complete, an efficiency measure is now included with most all our point configurations. Assuming it’s correct, the expanded efficiency table above shows the results.
The polyhedral vertex set – octahedron, cube, icosahedron and pentagonal dodecahedron surprised me. I had assumed the platonic solids were the only ideal solutions. The equidistant spacing of the vertices of the octahedron are the most ideal on the board - 0.908 - closest to one. What does the icosa’s greater than one value, 1.119 mean? Mediocre cube and dodeca values. I can see why the hoso’s are extinct.
The EQS precision set: 46, 130 and 406 are bold and highlighted. EQS238-0.846, and EQS312 – 0.849, would make better standards than EQS 130 and 406. I apologize for giving you grief over the rectangular plot algorithm which you converted to centroids. Given it’s overall values, I have a greater respect for the EQS algorithm and your implementation of it.

I claimed I could improve the efficiencies of some EQS solutions by adding an equatorial particle ring, or pole particles, rotating alternate equatorial or polar latitude rings, so I created a new spherical group scenario “EQS Mods” that shows such mods to EQS336: The result is a very respectable Mod EQS374 with efficiency value of 0.838. I didn’t quite follow the ‘dw centroids logic’ so I adjusted the latitudes by eye, trial and error. I need to work this with autocad and see if I can improve that number further.
Once again, the Golden algorithm has a poor and very linear efficiency result – it must be wrong. On the other hand, the new Kogan algorithm is as good as Golden. K201 or K326 would make fine standards.
The primary benefit of this table is that it provides sufficient justification in selecting a more efficient short list of precision alternatives.
Any thoughts? Feedback? Additional taskings?
.
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
I'm not sure how you are calculating those numbers. What equation are you using?
I spent a bit of time implementing a way to test the algorithms. I've pushed some new changes to do so, but there is no code that uses it yet. Here is what I have implemented:
We have some algorithms that generate points on the surface of a sphere, and we want to find the most even representation of that surface. We want each point to be of equal distance to its neighbours. In order to evaluate these algrithms, we must gather statistics about the data they generate.
In the first instance, our data is a series of points. We want to know how far each point is from all other points. For each point in the data set, we calculate the min, max, average and range of the distance to all other points. That gives us an array of min values, one for each point, and an array of max values, etc, etc.
That brings us to the second instance where we have a new data set containing statistics for each location generated by an algorithm. Statistics are addictive, you can't have just one, so let's gather some more statistics from the statistics that we already have.
Now we are analyzing each data set in isolation to the others. We are calculating the min, max, average and range of all mins, then all max values, then all averages and finally, all of the ranges. In the end, we reduce it all down to 16 numbers. Most of which are useless, but we'll get to that in a minute. This is what our final data set looks like:
Now we need to figure out which values mean something to this problem and help us to determine which is the better algorithm. Let's look at each data set and see what it is telling us.
Minimums:
The min data set can tell us how much deviation there is from true equality between points. This is a critical data set for this problem, as it represents the data we are trying to minimize between algorithms. Of particular interest is the range, which we want to approach zero. An algorithm that reached zero would have true equal distance between all points.
The min.min value represents the closest of all point pairs. This value ultimately comes from only 2 points in the original data set.
The min.max value represents the largest minimum of all point pairs. Same as with the min, only 2 points are used to calculate that value. This is the worst that the algorithm gets. Minimizing this value is important. We want min.min and min.max to approach each other.
The min.avg value represents the average minimum distance between points and gives us a general representation of an algorithm. This is probably a good value to initially look at to gauge algorithms. If you have to represent an algorithm with a single value, this is the one to use. While not exactly as important as others, it gives the best general idea of how an algorithm will perform.
Note that the min.avg value, and indeed all values really, heavily relies on the radius used. You must choose one radius and use it for all algorithms in order to be able to compare the numbers. A unit radius is generally the best.
The min.range value represents the difference between the smallest minimum and the largest minimum, therefore, it is a very important value. The closer this is to zero the better.
Maximums:
The max data set can tell us how balanced the points are on the sphere. In a truely balanced set of points, every point has an equal and opposite point from it. The line between those 2 points goes through the center of the sphere. The maximum value for any given point represents the point that is farthest from it. If that value equals the diameter of the sphere, then balance is achieved. If max.range also equals zero, then every point has an opposite.
This is not of important interest, and would not be used to differentiate algoithms in the first instance. If you have a few algorithms that appear equal, then this kind of balance may be used to differentiate them and choose a winner.
The max.min value represents the smallest maximum value.
The max.max value represents the largest maximum value.
The max.avg value represents the average maximum value.
The max.range value represents the difference between the largest maximum value and the smallest maximum value.
If max.avg equals the diameter and max.range equals zero then true balance is achieved.
Average:
The avg data set is of little use, but can be used like the max data set to determine balance. Since it is more dangerous to use as such, it can be ignored for this problem.
The avg.min value represents the smallest average value.
The avg.max value represents the largest average value.
The avg.avg value represents the average average value. Does that even mean something? I think we've gone too meta.
The avg.range value represents the difference between the largest average value and the smallest average value. It can be used to determine increasing uniformity as it approaches zero.
Range:
The range data set is not very important.
The range.min value represents the smallest range value.
The range.max value represents the largest range value.
The range.avg value represents the average range value. A good indicator of uniformity. The closer to zero the better.
The range.range value represents the difference between the largest range value and the smallest range value.
To analyze a set of algorithms, we calculate these values for each algorithm, using the same radius, and then put the important values into a table. Look at those values and see which algorithms look the best.
I have implemented a few new methods in the LocationCreator class to generate these statistics. I've even created a little helper method to just return the important ones, which are only 6 values out of 16. You need to implement each of the algorithms as a LocationCreator, just like you have with EQP. I suggest you copy the eqp.js file to a new file for each new algorithm, renaming each like algorithm-name.js, just like eqp.js and eqs.js, etc.
I'll look into creating a new modal dialog that will calculate the stats and present the results for all known algorithms in a table.
I spent a bit of time implementing a way to test the algorithms. I've pushed some new changes to do so, but there is no code that uses it yet. Here is what I have implemented:
Statistics of Points representing the Surface of a Sphere
We have some algorithms that generate points on the surface of a sphere, and we want to find the most even representation of that surface. We want each point to be of equal distance to its neighbours. In order to evaluate these algrithms, we must gather statistics about the data they generate.
In the first instance, our data is a series of points. We want to know how far each point is from all other points. For each point in the data set, we calculate the min, max, average and range of the distance to all other points. That gives us an array of min values, one for each point, and an array of max values, etc, etc.
That brings us to the second instance where we have a new data set containing statistics for each location generated by an algorithm. Statistics are addictive, you can't have just one, so let's gather some more statistics from the statistics that we already have.
Now we are analyzing each data set in isolation to the others. We are calculating the min, max, average and range of all mins, then all max values, then all averages and finally, all of the ranges. In the end, we reduce it all down to 16 numbers. Most of which are useless, but we'll get to that in a minute. This is what our final data set looks like:
- Code:
{
min: {
min: <number>,
max: <number>,
avg: <number>,
range: <number>
},
max: {
min: <number>,
max: <number>,
avg: <number>,
range: <number>
},
avg: {
min: <number>,
max: <number>,
avg: <number>,
range: <number>
},
range: {
min: <number>,
max: <number>,
avg: <number>,
range: <number>
}
}
Now we need to figure out which values mean something to this problem and help us to determine which is the better algorithm. Let's look at each data set and see what it is telling us.
Minimums:
The min data set can tell us how much deviation there is from true equality between points. This is a critical data set for this problem, as it represents the data we are trying to minimize between algorithms. Of particular interest is the range, which we want to approach zero. An algorithm that reached zero would have true equal distance between all points.
The min.min value represents the closest of all point pairs. This value ultimately comes from only 2 points in the original data set.
The min.max value represents the largest minimum of all point pairs. Same as with the min, only 2 points are used to calculate that value. This is the worst that the algorithm gets. Minimizing this value is important. We want min.min and min.max to approach each other.
The min.avg value represents the average minimum distance between points and gives us a general representation of an algorithm. This is probably a good value to initially look at to gauge algorithms. If you have to represent an algorithm with a single value, this is the one to use. While not exactly as important as others, it gives the best general idea of how an algorithm will perform.
Note that the min.avg value, and indeed all values really, heavily relies on the radius used. You must choose one radius and use it for all algorithms in order to be able to compare the numbers. A unit radius is generally the best.
The min.range value represents the difference between the smallest minimum and the largest minimum, therefore, it is a very important value. The closer this is to zero the better.
Maximums:
The max data set can tell us how balanced the points are on the sphere. In a truely balanced set of points, every point has an equal and opposite point from it. The line between those 2 points goes through the center of the sphere. The maximum value for any given point represents the point that is farthest from it. If that value equals the diameter of the sphere, then balance is achieved. If max.range also equals zero, then every point has an opposite.
This is not of important interest, and would not be used to differentiate algoithms in the first instance. If you have a few algorithms that appear equal, then this kind of balance may be used to differentiate them and choose a winner.
The max.min value represents the smallest maximum value.
The max.max value represents the largest maximum value.
The max.avg value represents the average maximum value.
The max.range value represents the difference between the largest maximum value and the smallest maximum value.
If max.avg equals the diameter and max.range equals zero then true balance is achieved.
Average:
The avg data set is of little use, but can be used like the max data set to determine balance. Since it is more dangerous to use as such, it can be ignored for this problem.
The avg.min value represents the smallest average value.
The avg.max value represents the largest average value.
The avg.avg value represents the average average value. Does that even mean something? I think we've gone too meta.
The avg.range value represents the difference between the largest average value and the smallest average value. It can be used to determine increasing uniformity as it approaches zero.
Range:
The range data set is not very important.
The range.min value represents the smallest range value.
The range.max value represents the largest range value.
The range.avg value represents the average range value. A good indicator of uniformity. The closer to zero the better.
The range.range value represents the difference between the largest range value and the smallest range value.
To analyze a set of algorithms, we calculate these values for each algorithm, using the same radius, and then put the important values into a table. Look at those values and see which algorithms look the best.
I have implemented a few new methods in the LocationCreator class to generate these statistics. I've even created a little helper method to just return the important ones, which are only 6 values out of 16. You need to implement each of the algorithms as a LocationCreator, just like you have with EQP. I suggest you copy the eqp.js file to a new file for each new algorithm, renaming each like algorithm-name.js, just like eqp.js and eqs.js, etc.
I'll look into creating a new modal dialog that will calculate the stats and present the results for all known algorithms in a table.
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
I have the statistics dialog up and running. It is comparing EQS, EQP and Hosohedron algorithms at the moment. The balance and uniformity both approach zero, so the lower the number, the better. The min, max and average can not be compared between algorithms, unless each algorithm has approximately the same number of points. So you can compare EQS 46 with EQP 46, or EQS 130 with EQP 130, etc. The range value is comparable across all and shows the variance of the algorithm. Closer to zero is better.
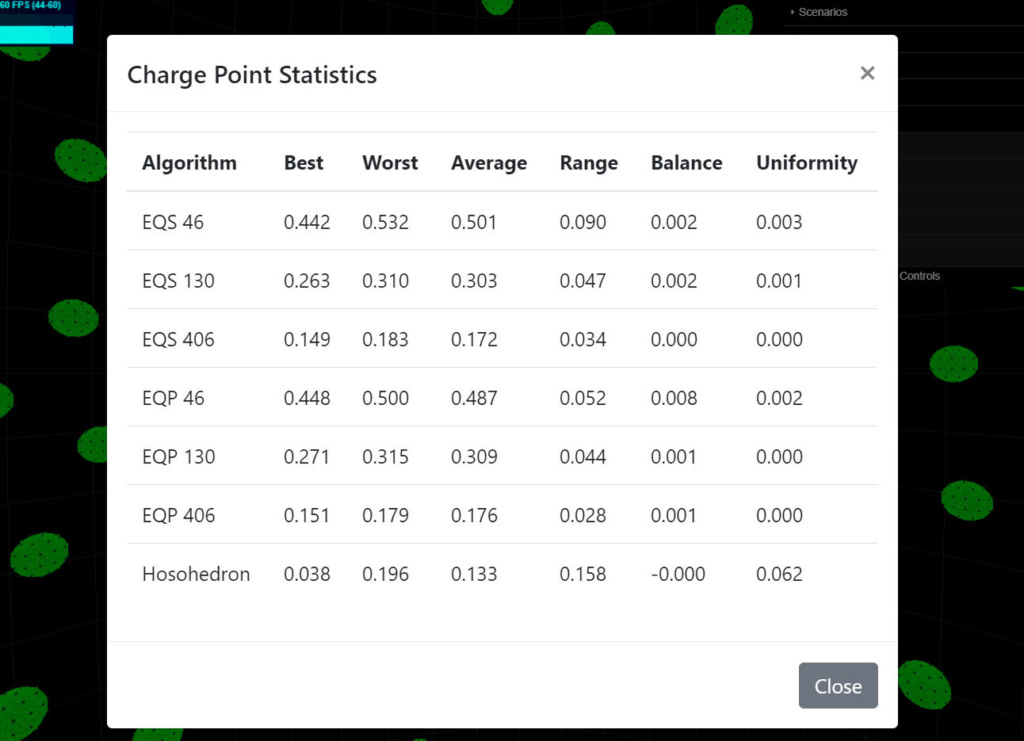
It shows your EQP improvements are very close to the standard EQS algorithm. I'm not sure what they look like, but the numbers look good. I created 3 versions to match the EQS variants. I'm not sure if they are good values or not. Have a look at the bottom of eqs.js to see what I did there. Play around with the numbers to try different options.

It shows your EQP improvements are very close to the standard EQS algorithm. I'm not sure what they look like, but the numbers look good. I created 3 versions to match the EQS variants. I'm not sure if they are good values or not. Have a look at the bottom of eqs.js to see what I did there. Play around with the numbers to try different options.
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
.
Nevyn wrote. I'm not sure how you are calculating those numbers. What equation are you using?
Airman. The efficiency measure numbers I’ve shown in my tables are the normalizedSmallestDistance[pts_].
normalizedSmallestDistance[pts_]:= smallestDistance[pts]/theoreticalsmallestDistance[length[pts_]]
var smallestDistance = minimum;
The only measured value is the smallestDistance, what you referred to as min-min.
var theoreticalSmallestDistance = radius * Math.sqrt((8*Math.PI)/((n)*(Math.sqrt(3))));
The theoreticalSmallestDistance provides an ideal value for any radius and number of particles. Please consider including it in your statistical set. It allows a way to measure across configuration sets – at a given radius and number of particles – as Kogan mentions in his paper.
Nevyn wrote. It shows your EQP improvements are very close to the standard EQS algorithm. I'm not sure what they look like, but the numbers look good. I created 3 versions to match the EQS variants. I'm not sure if they are good values or not. Have a look at the bottom of eqs.js to see what I did there. Play around with the numbers to try different options.
Airman. We have a disconnect. I’ve made no EQP improvements. I added the EQP set to the particle engine’s precision set two months ago. I added the above efficiency measure to the spherical group scenario EQP Points last month. I should point out, when one selects the ‘approximate number’ of EQP particles of 406 in the parameter tab, here’s the calculated output table:
Since that time, I’ve included the same efficiency measure in all the spherical configurations on their Output control tabs. My latest effort over the last day or two has been in trying to understand EQS var cellAngles well enough to modify it by adding new latitudes. To be honest, I want to throw out the angle and lastAngle averaging and list the desired particle latitudes directly, but that would be changing your centroid calculation.
In case of confusion; I had to give a quick reply lest you be working under a false assumption. I appreciate the stat breakdown and enthusiasm. I'd be happy to include any additional info on the user side of the firewall, on the output control tab’s output table if at all possible.
P.S. Added two same "and number of particles" as in; The theoreticalSmallestDistance provides an ideal value for any radius and number of particles.
.
Nevyn wrote. I'm not sure how you are calculating those numbers. What equation are you using?
Airman. The efficiency measure numbers I’ve shown in my tables are the normalizedSmallestDistance[pts_].
normalizedSmallestDistance[pts_]:= smallestDistance[pts]/theoreticalsmallestDistance[length[pts_]]
var smallestDistance = minimum;
The only measured value is the smallestDistance, what you referred to as min-min.
var theoreticalSmallestDistance = radius * Math.sqrt((8*Math.PI)/((n)*(Math.sqrt(3))));
The theoreticalSmallestDistance provides an ideal value for any radius and number of particles. Please consider including it in your statistical set. It allows a way to measure across configuration sets – at a given radius and number of particles – as Kogan mentions in his paper.
Nevyn wrote. It shows your EQP improvements are very close to the standard EQS algorithm. I'm not sure what they look like, but the numbers look good. I created 3 versions to match the EQS variants. I'm not sure if they are good values or not. Have a look at the bottom of eqs.js to see what I did there. Play around with the numbers to try different options.
Airman. We have a disconnect. I’ve made no EQP improvements. I added the EQP set to the particle engine’s precision set two months ago. I added the above efficiency measure to the spherical group scenario EQP Points last month. I should point out, when one selects the ‘approximate number’ of EQP particles of 406 in the parameter tab, here’s the calculated output table:
Only 404 particles.404 Neutrons. The configuration radius is 17.1. The smallest distance - between the centers of the two closest particles - is 2.581, between neutrons 1 and 2. The theoretical distance is 3.241. Smallest/Theoretical is 0.797.
Since that time, I’ve included the same efficiency measure in all the spherical configurations on their Output control tabs. My latest effort over the last day or two has been in trying to understand EQS var cellAngles well enough to modify it by adding new latitudes. To be honest, I want to throw out the angle and lastAngle averaging and list the desired particle latitudes directly, but that would be changing your centroid calculation.
In case of confusion; I had to give a quick reply lest you be working under a false assumption. I appreciate the stat breakdown and enthusiasm. I'd be happy to include any additional info on the user side of the firewall, on the output control tab’s output table if at all possible.
P.S. Added two same "and number of particles" as in; The theoreticalSmallestDistance provides an ideal value for any radius and number of particles.
.
Last edited by LongtimeAirman on Sat Apr 20, 2019 2:29 pm; edited 2 times in total (Reason for editing : Added P.S.)
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
I had another play with it and have the following table at the moment:
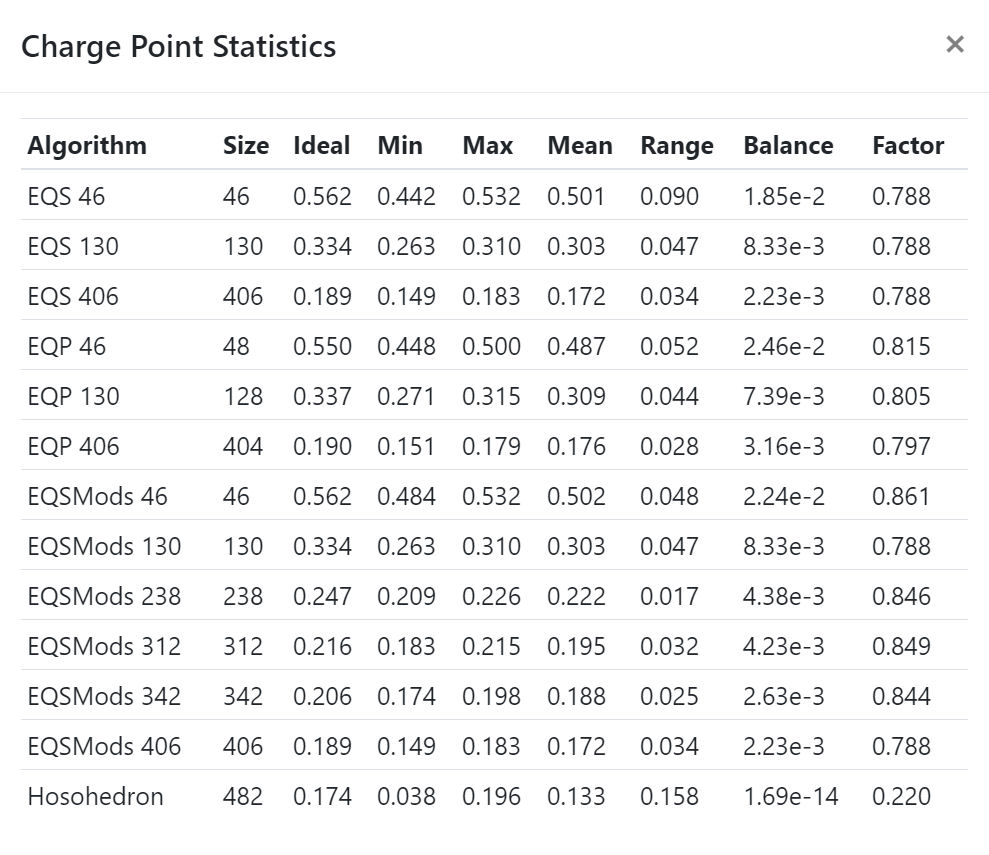
I combined the Balance and Uniformity fields together (and also changed the value being used for the uniformity), because I was out of space. Added in the sample size to show the actual number of points used. The Ideal column shows the theoretical smallest distance, using your equation. I haven't read up on it, so I don't know if it applies to all situations or just whatever Kogan was working on in that paper. The EQS algorithm beats it, though, so it seems to be limited.
I put the Ideal value right next to the Min and Max values, because that is what we want to compare it against. The last column, Factor, is Min/Ideal. I used the Min at first, but it didn't really work. I tried the Average and the results looked better to me. That is the average of the minimum values, so it represents all minimums rather than just the best minimum.
Here is the table using Average/Ideal:

We want to find an algorithm that has a low Range and Balance, and a Factor close to 1. The EQS algorithm is still looking the best to me. You're right about EQP, it isn't complete, but it does have some different cell angles being used. EQSMods is a new one where I extracted the cell angles from your spherical.js scenario, but then realised that the algorithm is different too, so it uses the angles, but not the new algorithm, just the standard EQS one.

I combined the Balance and Uniformity fields together (and also changed the value being used for the uniformity), because I was out of space. Added in the sample size to show the actual number of points used. The Ideal column shows the theoretical smallest distance, using your equation. I haven't read up on it, so I don't know if it applies to all situations or just whatever Kogan was working on in that paper. The EQS algorithm beats it, though, so it seems to be limited.
I put the Ideal value right next to the Min and Max values, because that is what we want to compare it against. The last column, Factor, is Min/Ideal. I used the Min at first, but it didn't really work. I tried the Average and the results looked better to me. That is the average of the minimum values, so it represents all minimums rather than just the best minimum.
Here is the table using Average/Ideal:

We want to find an algorithm that has a low Range and Balance, and a Factor close to 1. The EQS algorithm is still looking the best to me. You're right about EQP, it isn't complete, but it does have some different cell angles being used. EQSMods is a new one where I extracted the cell angles from your spherical.js scenario, but then realised that the algorithm is different too, so it uses the angles, but not the new algorithm, just the standard EQS one.
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
Please compare your ideal values against the two tables I posted, it's not there. As per the paper, I used the normalized value, smallest/theoretical. Give the paper a review, you'll see that a good normalized value is around 0.85.
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
This is the ideal value: Math.sqrt( ( 8 * Math.PI ) / ( numPoints * Math.sqrt( 3 ) ) )
I'm using a radius of 1, so it falls out. That is what you are referring to as the theoretical value. The Factor column contains first the smallest/theoretical, then the average smallest/theoretical in the second pic.
I'm using a radius of 1, so it falls out. That is what you are referring to as the theoretical value. The Factor column contains first the smallest/theoretical, then the average smallest/theoretical in the second pic.
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
.
With respect to precision alternatives, do we want to compare precision alternatives or do we want to provide a range of precision values? I favor the latter. Doing a quick review, I see the following current precision alternatives:
1. Low; 8 cardinal points octahedron;
2. Medium (K46);
3. High (K130);
4. Overdrive (K406);
5. EQP Medium (EQP46);
6. EQP High (EQP130); and
7. EQP Overdrive (EQP406).
In order to improve the range of our precision set consider:
EQP: We have EQP48 vice EQS46, EQP128 vice EQP130, and EQP404 vice EQP406 – none of the three EQP numbers agree with the EQS numbers to do a direct comparison, still, EQP128 may be slightly better than EQS13. More importantly, there doesn’t seem to be any good spherical alternatives between EQP46 and K201. So keep EQP128;
EQS: Keep EQS46, but drop EQS130. Add EQS 238 and/or EQS312. EQS406 has a low performance. The only alternative with a better performance near that number of particles would be my ModEQS374.
Kogan: Keep K46, but drop K130 and K406. Add K201 and K326.
That would make my proposed precision list:
1. Low; 8 cardinal points octahedron;
2. EQS46;
3. EQP128;
4. K201;
5. EQS238;
6. EQS312;
7. K326; and
8. ModEQS376;
.
Agreed. I think the Kogan spiral algorithm is prettier and provides numbers close to the equi-latitudinal/longitudinal area solutions of the EQS or EQP algorithms.Not sure if it is better or not, but it looks cool.
With respect to precision alternatives, do we want to compare precision alternatives or do we want to provide a range of precision values? I favor the latter. Doing a quick review, I see the following current precision alternatives:
1. Low; 8 cardinal points octahedron;
2. Medium (K46);
3. High (K130);
4. Overdrive (K406);
5. EQP Medium (EQP46);
6. EQP High (EQP130); and
7. EQP Overdrive (EQP406).
In order to improve the range of our precision set consider:
EQP: We have EQP48 vice EQS46, EQP128 vice EQP130, and EQP404 vice EQP406 – none of the three EQP numbers agree with the EQS numbers to do a direct comparison, still, EQP128 may be slightly better than EQS13. More importantly, there doesn’t seem to be any good spherical alternatives between EQP46 and K201. So keep EQP128;
EQS: Keep EQS46, but drop EQS130. Add EQS 238 and/or EQS312. EQS406 has a low performance. The only alternative with a better performance near that number of particles would be my ModEQS374.
Kogan: Keep K46, but drop K130 and K406. Add K201 and K326.
That would make my proposed precision list:
1. Low; 8 cardinal points octahedron;
2. EQS46;
3. EQP128;
4. K201;
5. EQS238;
6. EQS312;
7. K326; and
8. ModEQS376;
.
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
The Kogan algorithm can use any number of points. I chose those ones to match the EQS algorithm and get a feel for how they worked at the same size. If we choose to use that algorithm, we can see what number of points works best. I don't want to mix-and-match algorithms, with the exception of the first precision. I just want one that works well across a few precision points. We might find that the Kogan algorithm works well at 200, 400 and 600, or 100, 200, 400, for example.
There are still some issues at the poles. Not quite as bad as EQS and no where near as bad as most algorithms, but it is still there.
There are still some issues at the poles. Not quite as bad as EQS and no where near as bad as most algorithms, but it is still there.
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
.
You're the boss, I try to be self-motivating, but at the moment, I need directions.
If you agree, I'll load all the additional stats you've included with the new Statistics button in all the spherical scenarios Output control tab's Output table. That will enable us to collect the same data for every n of every spherical algorithm for direct comparison.
Feel free to direct or task me otherwise.
.
You're the boss, I try to be self-motivating, but at the moment, I need directions.
If you agree, I'll load all the additional stats you've included with the new Statistics button in all the spherical scenarios Output control tab's Output table. That will enable us to collect the same data for every n of every spherical algorithm for direct comparison.
Feel free to direct or task me otherwise.
.
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
You can add it to those scenarios if you want, but it will be easier to create another button that targets a specific algorithm and generates the stats for a range of sizes. We can't do that with EQS, but we can with Kogan. I'll look into that over the next few days.
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
.
The Charge Point Statistics button includes 9 items: Algorithm, Size, Ideal, Min, Max, Mean, Range, Balance, and Factor. In order to match the Statistics button output, the spherical scenarios efficiency calculations would need to rename four variables and add four new output variables: Max, Mean, Range, and Balance. So, thanks for clarification, other than changing names, I won’t be adding new values at present.
Still, I made good progress - for me. Working with point sets are fun. Each algorithm had its own set of efficiency calculations. I replaced those instances with function calls to a single instance; function calcStats( num, radius, xPts, yPts, zPts ). I changed most all the verbiage to agree with the Statistics button. Now, if you give the word, I can work on adding or changing all the spherical scenario Output tables in one place. I’ll push the change in a few hours.
Next, each algorithm has two instances of point set creations, for both statistics and particle placement. I suppose I should reduce that to just one functional point creation instance and two function calls (for each algorithm). It adds up.
.
Thanks for calling me off, but a few changes are necessary. Such as conforming my prior efficiency verbiage to agree with the new statistics data.You can add it to those scenarios if you want, but it will be easier to create another button ... .
The Charge Point Statistics button includes 9 items: Algorithm, Size, Ideal, Min, Max, Mean, Range, Balance, and Factor. In order to match the Statistics button output, the spherical scenarios efficiency calculations would need to rename four variables and add four new output variables: Max, Mean, Range, and Balance. So, thanks for clarification, other than changing names, I won’t be adding new values at present.
Still, I made good progress - for me. Working with point sets are fun. Each algorithm had its own set of efficiency calculations. I replaced those instances with function calls to a single instance; function calcStats( num, radius, xPts, yPts, zPts ). I changed most all the verbiage to agree with the Statistics button. Now, if you give the word, I can work on adding or changing all the spherical scenario Output tables in one place. I’ll push the change in a few hours.
Next, each algorithm has two instances of point set creations, for both statistics and particle placement. I suppose I should reduce that to just one functional point creation instance and two function calls (for each algorithm). It adds up.
.
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
.
Maybe we can plot the Kogan values off of the list you’re generating with the Statistics2 button?
Good progress today, I'll push the changes in a couple of hours. As hoped, I successfully converted the two instances of code creating point sets within each algorithm – for particle placement or distribution calculations – into two function calls, and one instance of function coding. I also corrected a problem with Poly points and calcStats that I pushed yesterday.
All the spherical configuration scenarios are now better organized. For example, it occurs to me I should create a single scenario where I can output any spherical set, just provide the desired: typeAlgorithm, number of surface particles, and configuration radius. Or I can put two or more configurations on the screen at once.
.
Maybe we can plot the Kogan values off of the list you’re generating with the Statistics2 button?
Good progress today, I'll push the changes in a couple of hours. As hoped, I successfully converted the two instances of code creating point sets within each algorithm – for particle placement or distribution calculations – into two function calls, and one instance of function coding. I also corrected a problem with Poly points and calcStats that I pushed yesterday.
All the spherical configuration scenarios are now better organized. For example, it occurs to me I should create a single scenario where I can output any spherical set, just provide the desired: typeAlgorithm, number of surface particles, and configuration radius. Or I can put two or more configurations on the screen at once.
.
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
.
Currently, all the spherical configuration scenario’s surface particles share the same orientation - they are all aligned with the world coordinates. Turn on the Boundary and Particle axes graphics to see that all particle axes: n/s (y-axis, green), e/w (x-axis, red) and f/b (z-axis, blue), are parallel. I want to re-orient/rotate all the surface particles such that their n/s axis is pointed to the configuration center – the (0,0,0) position. The particles would then be aligned to the spherical configuration instead of the world. By adding a checkbox, the user can choose to align the particles one way or the other.

Each particle has a different, but not correct, orientation.
Of course, reorienting each particle properly is easier said than done. Adding insult to injury, quaternions are built into three.js, but I haven’t figured out how to make them work for this problem yet. The image above shows EQP46 particles improperly reoriented by this codeline –
var q = new THREE.Quaternion().setFromAxisAngle( new THREE.Vector3( points[i].x, points[i].y, points[i].z ), angle*i ); // angle = 2PIRad/number of particles.
I believe I need to do three cross products between each position and each axis. Then follow that up with three dot products to determine the angles. I’ve suffered this problem long enough to seek help. Here are two recent finds I must share:
Rotation Quaternions, and How to Use Them, by D. Rose - May, 2015. Short and straightforward, this paper includes a three step quaternion rotation process. Step 1: Convert the point to be rotated into a quaternion by assigning the point's coordinates as the quaternion's imaginary components, … . Step 2: Perform the rotation. … . Step 3: Extract the rotated coordinates from p'. ... .
3d Math Primer for Graphics and Game Development, Fletcher Dunn and Ian Parberry – 2nd edition, 2011. A wonderful ‘basics’ math book that I’ve always wanted. All you need - including physics - to create your own particle engine. As I understand it, this is a free e-book, in pdf, or you may choose to purchase a printed copy. Check it out.
.
Currently, all the spherical configuration scenario’s surface particles share the same orientation - they are all aligned with the world coordinates. Turn on the Boundary and Particle axes graphics to see that all particle axes: n/s (y-axis, green), e/w (x-axis, red) and f/b (z-axis, blue), are parallel. I want to re-orient/rotate all the surface particles such that their n/s axis is pointed to the configuration center – the (0,0,0) position. The particles would then be aligned to the spherical configuration instead of the world. By adding a checkbox, the user can choose to align the particles one way or the other.

Each particle has a different, but not correct, orientation.
Of course, reorienting each particle properly is easier said than done. Adding insult to injury, quaternions are built into three.js, but I haven’t figured out how to make them work for this problem yet. The image above shows EQP46 particles improperly reoriented by this codeline –
var q = new THREE.Quaternion().setFromAxisAngle( new THREE.Vector3( points[i].x, points[i].y, points[i].z ), angle*i ); // angle = 2PIRad/number of particles.
I believe I need to do three cross products between each position and each axis. Then follow that up with three dot products to determine the angles. I’ve suffered this problem long enough to seek help. Here are two recent finds I must share:
Rotation Quaternions, and How to Use Them, by D. Rose - May, 2015. Short and straightforward, this paper includes a three step quaternion rotation process. Step 1: Convert the point to be rotated into a quaternion by assigning the point's coordinates as the quaternion's imaginary components, … . Step 2: Perform the rotation. … . Step 3: Extract the rotated coordinates from p'. ... .
3d Math Primer for Graphics and Game Development, Fletcher Dunn and Ian Parberry – 2nd edition, 2011. A wonderful ‘basics’ math book that I’ve always wanted. All you need - including physics - to create your own particle engine. As I understand it, this is a free e-book, in pdf, or you may choose to purchase a printed copy. Check it out.
.
LongtimeAirman- Admin
- Posts : 2078
Join date : 2014-08-10
 Re: Possible Charged Particle Field
Re: Possible Charged Particle Field
To rotate an object to point towards a specific point:
Let:
p1 = center point of object
p2 = point to look towards
Let:
p1 = center point of object
p2 = point to look towards
- Code:
// create a vector to represent the line from p1 to the point on the object that needs to be oriented towards p2
// I think this will be the Y axis for you
var align = new THREE.Vector3( 0, 1, 0 );
// calculate the vector between the location of the object and the target point
// this is where align will end up at the end of this algorithm
var v = new THREE.Vector3().subVectors( p1, p2 );
// calculate the angle between those 2 vectors
var angle = align.angleTo( v );
// calculate axis to rotate around
// this is the vector that is orthogonal to both align and v
var axis = new THREE.Vector3().crossVectors( align, v ).normalize();
// create quaternion to represent the rotation
var quat = new THREE.Quaternion().setFromAxisAngle( axis, angle );
// apply quaternion to object
...
Page 14 of 15 •  1 ... 8 ... 13, 14, 15
1 ... 8 ... 13, 14, 15 
 Similar topics
Similar topics» Modeling a Charge Particle
» Spinning Particle Language
» Particle Drifts in Space
» The First Ever Photograph of Light as both a Particle and Wave
» Physicists Finally Narrowed Down the Mass of the Tiniest 'Ghost Particle' in the Universe
» Spinning Particle Language
» Particle Drifts in Space
» The First Ever Photograph of Light as both a Particle and Wave
» Physicists Finally Narrowed Down the Mass of the Tiniest 'Ghost Particle' in the Universe
Page 14 of 15
Permissions in this forum:
You cannot reply to topics in this forum
